Самый верхний многоугольник из набора ребер

Предположим, у меня есть набор 2d линейных сегментов, которые все связаны. Мне нужен алгоритм, который находит самые внешние сегменты в наборе. То есть минимальное подмножество, которое ограничивает ту же область.

Примечание: это не то же самое, что нахождение выпуклой оболочки точек, составляющих сегменты.

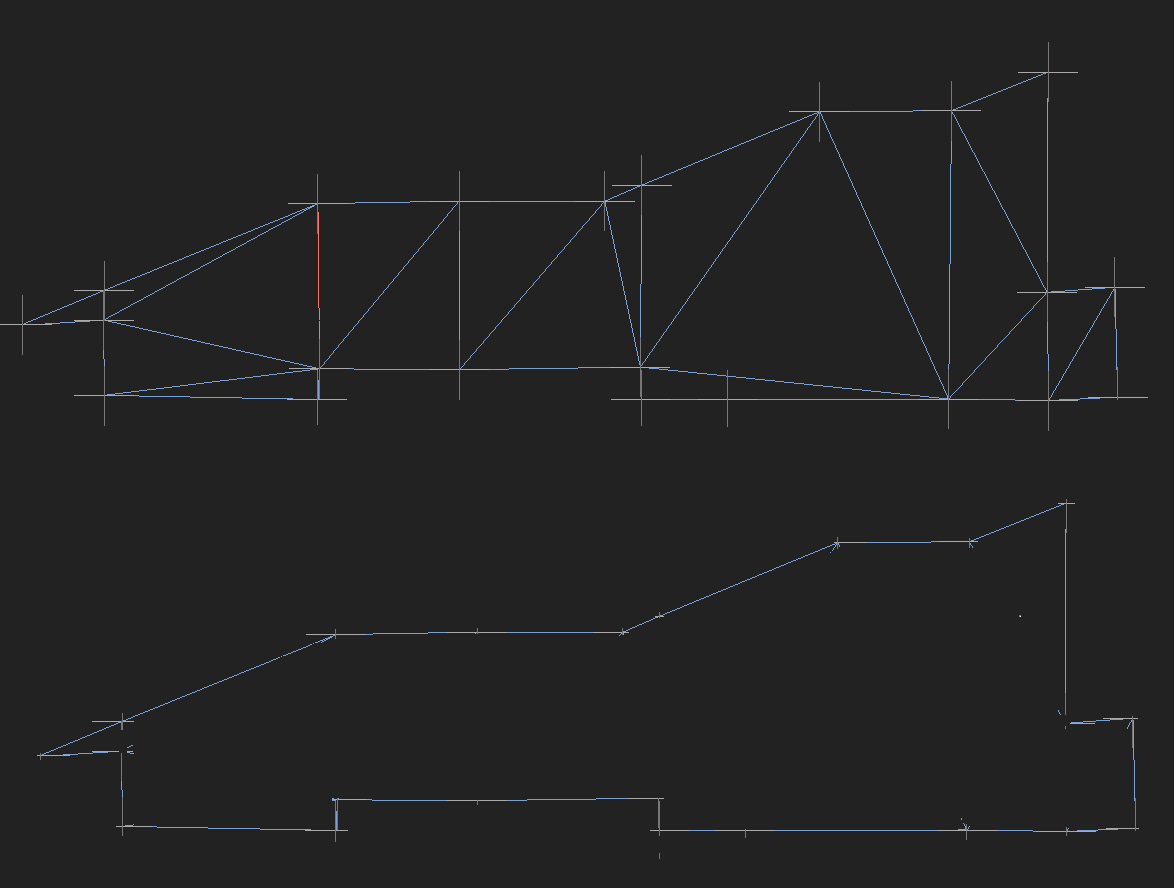
Редактировать: вверху находится начальный набор сегментов. Ниже тот же контур с удаленными внутренними сегментами. (Игнорируйте маленькие серые крестики, они просто обозначают точки пересечения.)

Источник

3 ответа

Решение

Как бы вы сделали это с карандашом...?

  1. Найдите крайнюю левую вершину (минимум х). Если их больше одного, выберите самый низкий из них (минимум у). Нет вершины ниже текущей, поэтому в качестве ориентира выберите направление "вниз".
  2. Найдите все ребра, идущие от текущей вершины, и рассчитайте их направления (опоры). Найти тот, который делает наименьший положительный угол (против часовой стрелки) от опорного направления. Это будет контурный сегмент.
  3. Выбрать другой конец в качестве нового "текущей" вершины и задать направление от этой вершины до последнего места в качестве нового опорного направления.
  4. Продолжайте с шага 2, пока не дойдете до начальной вершины.
  5. Удалить все не посещенные сегменты.
  6. Удалите все осиротевшие вершины (если они появились на шаге 5).
Источник

Для заданного триангулированного невыпуклого многоугольника можно указать направление обхода вершин (по часовой стрелке против часовой стрелки). Сделайте так, чтобы все треугольники были одинаково ориентированы WRT-обход его вершин. Разложите все треугольники на направленные ребра. Каждое ребро для каждого треугольника - это кортеж из двух вершин (a, b), Для каждого соседнего треугольника у вас есть два противоположных ребра (a, b) а также (b, a), Вы можете просто исключить такие пары ребер из дальнейшего рассмотрения. Наконец вы получите набор исключительно внешних ребер.

Нет потери общности, если ваш многоугольник состоит из не симплициальных частей (но все же вы можете указать направление обхода вершин).

Триангуляция построенного исходного сегмента многоугольника является очевидным шагом: растягивание вершин на $d + 1$ параболоид и триангуляция, затем исключение треугольников, содержащих по крайней мере одно ребро, которое не соответствует ни одному исходному сегменту.

Другой возможный подход - слегка модифицированный алгоритм упаковки подарков.

Источник

Далее следует подход, который начинается с выпуклой оболочки, а затем направляется внутрь. Интуиция заключается в том, что вы начинаете с ребер на корпусе, затем заполняете пробелы, находя ближайшую точку "вдоль" пробела, следуя кратчайшему пути в наборе ребер.

  1. Вычислить выпуклую оболочку ваших точек.
  2. Пересечь набор корпуса с вашим набором ребер. Это оставит вас с рядом потенциально отключенных краевых путей.
  3. Любая точка, которая не имеет двух ребер (т. Е. Лист в терминах графа), соединяется со своим ближайшим листом путем нахождения кратчайшего пути в исходном наборе ребер.
  4. Любые связи могут быть разорваны путем, который образует наименьшую площадь при закрытии корпусом.
Источник
Другие вопросы по тегам