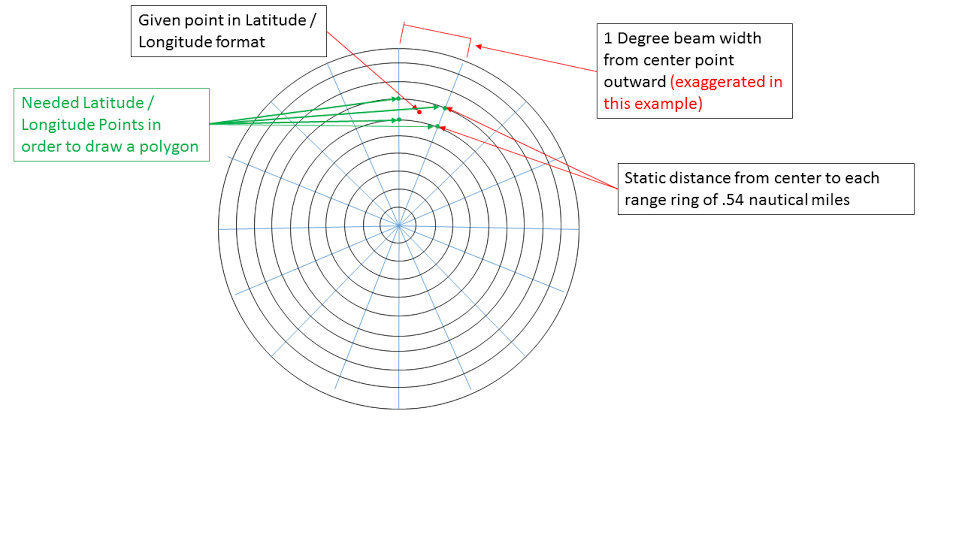
Геометрия радиальной координаты в декартову с ограничивающими точками

Question

Мне нужно найти 4 точки в формате Широта / Долгота, окружающие данную центральную точку и полученный алгоритм (если это возможно).

Известная информация: Равные расстояния для каждой "корзины" от центра точки (радара) наружу. Пример = .54 морских миль.

Ширина луча 1 градус. Центральная точка "мусорного ведра"

Это изображение в полярных координатах (я думаю, что это похоже на радиальные координаты???):

Мне нужно преобразовать полярный / радиальный в декартову, и я смогу сделать это с помощью этой формулы.

x = r × cos (θ) y = r × sin (θ)

Так что теперь все, что мне нужно сделать, это найти контурные координаты "бина" (4 угла), чтобы я мог нарисовать многоугольник в декартовом пространстве координат.

Я использую Delphi/Pascal для кодирования, но я могу преобразовать другие языки, если у вас есть пример алгоритма.

Спасибо за любые предложения или примеры алгоритмов. С уважением, Брайан

Answer 1

Вам необходимо преобразовать все в одну и ту же систему координат, а затем наложить критерии расстояния следующим образом:

1. Преобразуйте вашу центральную точку из географических координат в полярные координаты, чтобы получить (r _C, θ _C)
2. Преобразуйте вашу центральную точку из полярных в декартовые координаты, используя уравнения, получая

3. Угловые точки с правой стороны от центральных точек (x _R, y _R) удовлетворяют уравнению

   (x _R - x _C) ² + (y _R - y _C) ² = D ²

   [r _R cos (θ _C +0,5 ^o) - x _C ] ² + [r _R sin (θ _C +0,5 ^o) - y _C ] ² = D ²

где D= расстояние между центральной точкой и угловыми точками

В вышеприведенном уравнении известно все, кроме r _R. Это должно привести к квадратному уравнению с двумя решениями, которые вы можете легко решить. Это ваши две угловые точки на правой стороне.

4. Повторите шаг 3 с углом θ _C -0,5 ^o, чтобы получить угловые точки с левой стороны.