Создание трехмерной кривой Гильберта с заполнением пространства с использованием графики черепах

Question

У меня есть алгоритм, основанный на графике черепах, для генерации заполняющей пространство кривой Гильберта в двух измерениях. Это рекурсивно и выглядит так:

Хотите нарисовать кривую порядка n в направлении x (где x ∈ {L, R}), и разреши y быть направлением, противоположным x, Мы делаем следующее:

• повернуть в направлении y
• нарисовать гильбертову кривую порядка n-1 направление y
• сделать шаг вперед
• повернуть в направлении x
• нарисовать гильбертову кривую порядка n-1 направление x
• сделать шаг вперед
• нарисовать гильбертову кривую порядка n-1 направление x
• повернуть в направлении x
• сделать шаг вперед
• нарисовать гильбертову кривую порядка n-1 направление y

Я понял это и смог реализовать рабочее решение. Тем не менее, я сейчас пытаюсь "обновить" это до 3D, и вот где я в основном ударил стену; в 3D, когда мы достигаем вершины, мы можем поворачиваться не в двух, а в четырех направлениях (прямое движение или движение назад, очевидно, не вариант, следовательно, четыре, а не шесть). Интуитивно, я думаю, я должен хранить самолет, на котором "ходит" черепаха, и его общее направление в мире, представленное enum с шестью значениями:

• вверх
• вниз
• Оставил
• Правильно
• В (с точки зрения камеры, он идет "внутри" мира)
• Out (так же, как выше, снаружи)

Черепаха, как и в 2D, имеет состояние, содержащее информацию, изложенную выше, и когда она достигает вершины (которую можно рассматривать как "пересечение"), она должна принять решение, куда идти дальше, основываясь на этом состоянии. В то время как в двух измерениях это довольно просто, в трех, я в тупике.

1. Мой подход правильный? (т.е. это то, что я должен хранить в состоянии черепахи?)
2. Если да, то как я могу использовать эту информацию, чтобы принять решение, куда идти дальше?

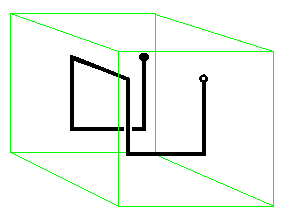
Поскольку существует много вариантов заполнения трехмерного пространства кривыми Гильберта, я должен указать, что это то, что я использую в качестве справочного материала и чтобы помочь моему воображению:

Мне известно, что подобный вопрос уже задавался, но в принятых ответных ссылках на веб-сайт эта проблема решается с использованием другого подхода (то есть, не графика черепахи).

Answer 1

Ваш двумерный алгоритм может быть обобщен как "LRFL" или "RLFR" (с "F", являющимся "вперед"). Каждая буква означает "поверните это направление, нарисуйте (n-1)-кривую в этом направлении и сделайте шаг вперед". (Это предполагает x на шаге 8 должно быть y.)

В 3d вы можете суммировать алгоритм за 7 ходов, которые вам понадобятся, чтобы идти по вашей ссылке. Это будет зависеть от того, как вы визуализируете запуск черепахи. Если он начинается с пустого круга, обращенного к заполненному кругу и направленного вверх (спиной вверх), то ваша ссылка будет "DLLUULL".