Пересечение 3 кругов, которые находятся на одной линии - трилатерация

Question

Я столкнулся с проблемой: я хотел бы вычислить пересечение трех кругов. Насколько мне известно, я должен использовать так называемое Трилатерация. Я реализовал это в C++. В статье говорится, что есть три ограничения этого решения.

1. все три центра находятся в плоскости z = 0,
2. центр сферы, P1, находится в начале координат,
3. и центр сферы, P2, находится на оси X

Что касается первого "критерия", мне нечего делать, потому что все три центра находятся в плоскости z = 0, поскольку я не использую координаты Z. После этого я перевел точки в позиции, где центр первой точки (P1) находится в начале координат. После этого я повернул точку P2 (и P3 тоже) в положение, где P2 находится на оси X.

Моя проблема: когда все три центра находятся на оси X, я попытался вычислить центр области пересечения (который вычисляется с использованием алгоритма статьи вики), но вычисление сделать невозможно. С другой стороны, нет ограничения, которое говорит что-то вроде "центры кругов не могут быть на одной линии... Давайте посмотрим на мою проблему визуально, я просто нарисовал ее:

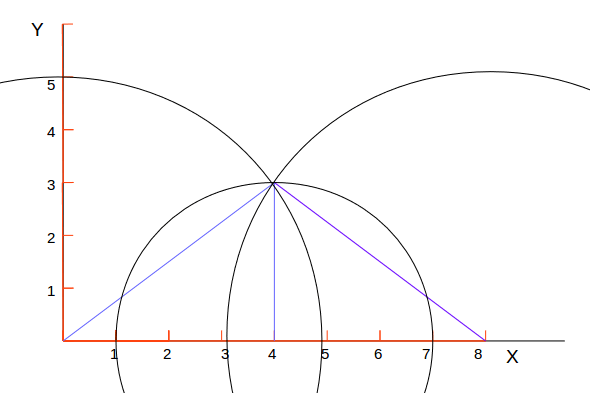
Как видите, три окружности пересекаются друг с другом в одной точке в координатах (4,3). Поэтому существует решение для этих точек, которые находятся на одной линии (в этом примере, на оси x). Параметры окружностей следующие (x,y, радиус):

P1: (0,0,5)
P2: (4,0,3)
P3: (8,0,5)

Как я уже упоминал, я успешно реализовал алгоритм трилатерации, но он не может решить этот пример, в результате получается NaN (не число). Конечно, я уже пробовал этот алгоритм с другими кругами (которые не находятся на одной линии), и он работает правильно.

Поэтому я начал отлаживать свою реализацию и обнаружил, в чем проблема. Моя реализация заключается в следующем:

#include <iostream>
#include <fstream>
#include <sstream>
#include <math.h> 
#include <vector>
std::ifstream infile("coordinateList.txt");
using namespace std;

std::vector<double> trilateration2D(double point1[], double point2[], double point3[], double r1, double r2, double r3) {
    std::vector<double> resultPose;
    //unit vector in a direction from point1 to point 2
    double p2p1Distance = pow(pow(point2[0]-point1[0],2) + pow(point2[1]-point1[1],2),0.5);
    double exx = (point2[0]-point1[0])/p2p1Distance;
    double exy = (point2[1]-point1[1])/p2p1Distance;

    //signed magnitude of the x component
    double ix = exx*(point3[0]-point1[0]);
    double iy = exy*(point3[1]-point1[1]);
    double i = ix+iy;
    //the unit vector in the y direction. 
    double eyx = (point3[0]-point1[0]-ix*exx)/pow(pow(point3[0]-point1[0]-ix*exx,2) + pow(point3[1]-point1[1]-iy*exy,2),0.5);
    double eyy = (point3[1]-point1[1]-iy*exy)/pow(pow(point3[0]-point1[0]-ix*exx,2) + pow(point3[1]-point1[1]-iy*exy,2),0.5);
    //the signed magnitude of the y component
    double jx = eyx*(point3[0]-point1[0]);
    double jy = eyy*(point3[1]-point1[1]);
    double j = jx + jy;
    //coordinates
    double x = (pow(r1,2) - pow(r2,2) + pow(p2p1Distance,2))/ (2 * p2p1Distance);
    double y = (pow(r1,2) - pow(r3,2) + pow(i,2) + pow(j,2))/(2*j) - i*x/j;
    //result coordinates
    double finalX = point1[0]+ x*exx + y*eyx;
    double finalY = point1[1]+ x*exy + y*eyy;
    resultPose.push_back(finalX);
    resultPose.push_back(finalY);
    return resultPose;
}
int main(int argc, char* argv[]){
    std::vector<double> finalPose;
    double p1[] = {0,0};
    double p2[] = {4,0};
    double p3[] = {8,0};
    double r1,r2,r3;
    r1 = 5;
    r2 =3;
    r3 = 5;
    finalPose = trilateration2D(p1,p2,p3,r1,r2,r3);
    cout<<"X:::  "<<finalPose[0]<<endl;
    cout<<"Y:::  "<<finalPose[1]<<endl;

}

Когда программа вычисляет EYX и EYY, в делении есть нули, и, разумеется, деление на ноль "не допускается". EYX и EYY - это единичные векторы в направлении y, но при таком расположении окружностей нет единичного вектора в направлении y.

Мой вопрос: есть ли 4-е ограничение этого алгоритма? На мой взгляд, это было бы написано в статье, поэтому: не могли бы вы посоветовать другое решение этой проблемы, где пересечение может быть рассчитано, когда все точки находятся на одной линии? Заранее спасибо!