Выборка положительных весов с суммой единства и ограничением равенства

Предположим, у меня есть вектор положительных весов a=(a1, a2, a3, a4) такой, что a2=a3 а также a1+a2+a3+a4=1, Можно ли как-нибудь отобрать этот вес с помощью R? Я пытался подумать об использовании распределения Дирихле, но оно не дает механизма, чтобы заставить два из переменных быть равными.

Источник

2 ответа

Решение

Равномерно пробовать по всему набору {(a1, a2, a3, a4 | a2=a3, a1+a2+a3+a4=1, a1>0, a2>0, a3>0, a4>0}, Я бы сначала сэмплировал значение для a2 (что равно a3). Для этого нам нужно знать распределение этого значения. Если a2 = a3 = rтогда мы имеем a1+a4 = 1-2r; для положительных а1 и а4 есть отрезок длины (1-2k)*sqrt(2) содержащий все возможные значения a1 а также a4, Интегрирование, вероятность того, что a2 является k или меньше 4(k - k^2), Более подробно:

Prob (a2 <= k) = Integral(0 to k) (1-2r)*sqrt(2) dr / Integral(0 to 0.5) (1-2r)*sqrt(2) dr
               = ((k-k^2)*sqrt(2)) / (sqrt(2)/4)
               = 4k - 4k^2

Таким образом, мы можем выбрать значения для a2 выбрав равномерно распределенное значение u~U(0, 1) и настройка a2 чтобы равняться значению k для которого 4k - 4k^2 = u, Решая с помощью квадратной формулы, это дает:

a2 = 0.5 * (1 - sqrt(1-u))

В R мы можем выбрать 1000 значений для a2 с:

set.seed(144)
a2 <- 0.5 * (1 - sqrt(1 - runif(1000)))
a3 <- a2

Учитывая фиксированное значение a2 = a3 = k, значение a1 равномерно распределен в [0, 1-2k]:

a1 <- runif(1000) * (1 - 2*a2)

Уточнив a1, a2, а также a3есть только одно возможное значение для a4:

a4 <- 1 - a1 - a2 - a3

Мы можем взглянуть на некоторые из наших выборочных значений:

head(cbind(a1, a2, a2, a4))
#              a1         a2         a2         a4
# [1,] 0.83455239 0.01251016 0.01251016 0.14042729
# [2,] 0.02744599 0.22932773 0.22932773 0.51389856
# [3,] 0.45835472 0.23860119 0.23860119 0.06444291
# [4,] 0.36843649 0.14679703 0.14679703 0.33796946
# [5,] 0.35109881 0.08702039 0.08702039 0.47486041
# [6,] 0.02916818 0.19942616 0.19942616 0.57197949

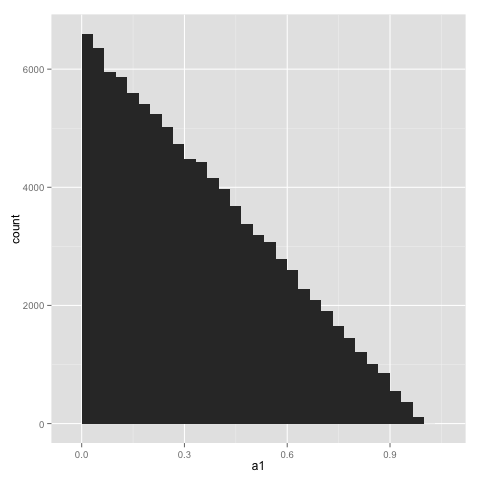
Вот распределение a1 значения (обратите внимание, что по симметрии это идентично распределению a4 ценности). Потому что мы выбираем a1 равномерно в диапазоне [0, 1-2*a2]более низкие значения встречаются чаще, чем более высокие:

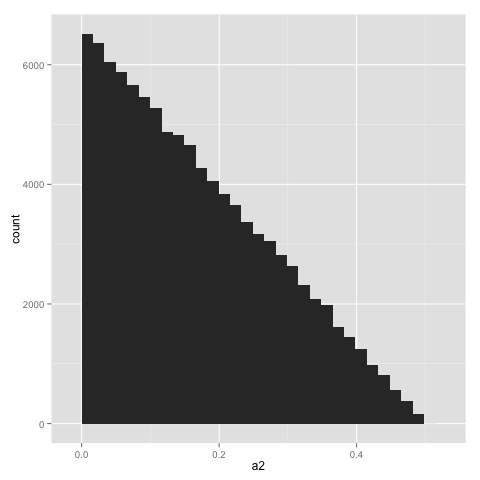
Вот распределение a2 значения (по определению это то же самое, что и распределение a3 ценности). Форма распределения похожа на a1, но максимальное значение составляет 0,5:

Источник

Я пытался подумать об использовании дистрибутива Dirichlet,

Ну, для меня это выглядит как распределение Дирихле.

но это не дает никакого механизма, чтобы заставить два из переменных быть равными.

но ты не обязан. На самом деле у вас есть три вариации из распределения Дирихле - A, B, C, все>= 0, равномерно распределенные U(0,1), так что A+B+C=1

После выборки (A, B, C) вы просто назначаете

a1 = A;
a2 = B/2.0;
a3 = B/2.0;
a4 = C;

Посмотрите, пожалуйста, как это сделать (ну, в Python)

Генерация N равномерных случайных чисел, сумма которых равна M

Источник
Другие вопросы по тегам