Scipy's Оптимизировать пределы соответствия кривой

Есть ли какой-нибудь способ, которым я могу предоставить ограничения для Оптимизации Кривой Сципиона?

Мой пример:

    def optimized_formula(x, m_1, m_2, y_1, y_2, ratio_2):
        return (log(x[0]) * m_1 + m_2)*((1 - x[1]/max_age)*(1-ratio_2)) + ((log(x[1]) * y_1 + y_2)*(x[1]/max_age)*ratio_2)

    popt, pcov = optimize.curve_fit(optimized_formula, usage_and_age, prices)

x [0] - это возраст, а max_age - это константа. Имея это в виду, когда x [0] приближается к максимуму, x [1] / max_age приближается к 1.

Можно ли обеспечить ограничение / лимит, при котором x[1]/max_age > 0,3 и x[1]/max_age < 0,7 и другие ограничения, такие как m_1 < 0, m_2 > 0 и т. Д.

Источник

4 ответа

Решение

Как предлагается в другом ответе, вы можете использовать lmfit для такого рода проблем. Поэтому я добавляю пример того, как его использовать, если кто-то также заинтересован в этой теме.

Допустим, у вас есть набор данных следующим образом:

xdata = np.array([177.,180.,183.,187.,189.,190.,196.,197.,201.,202.,203.,204.,206.,218.,225.,231.,234.,
          252.,262.,266.,267.,268.,277.,286.,303.])

ydata = np.array([0.81,0.74,0.78,0.75,0.77,0.81,0.73,0.76,0.71,0.74,0.81,0.71,0.74,0.71,
      0.72,0.69,0.75,0.59,0.61,0.63,0.64,0.63,0.35,0.27,0.26])

и вы хотите подогнать модель к данным, которая выглядит следующим образом:

model = n1 + (n2 * x + n3) * 1./ (1. + np.exp(n4 * (n5 - x)))

с ограничениями, которые

0.2 < n1 < 0.8
-0.3 < n2 < 0

С помощью lmfit (версия 0.8.3) вы получите следующий вывод:

n1:   0.26564921 +/- 0.024765 (9.32%) (init= 0.2)
n2:  -0.00195398 +/- 0.000311 (15.93%) (init=-0.005)
n3:   0.87261892 +/- 0.068601 (7.86%) (init= 1.0766)
n4:  -1.43507072 +/- 1.223086 (85.23%) (init=-0.36379)
n5:   277.684530 +/- 3.768676 (1.36%) (init= 274)

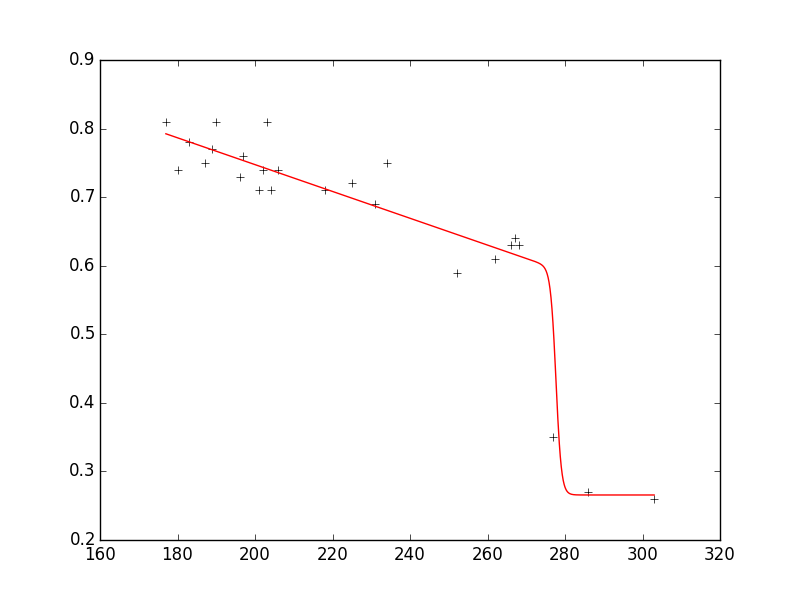
Как видите, подгонка очень хорошо воспроизводит данные, а параметры находятся в запрошенных диапазонах.

Вот весь код, который воспроизводит сюжет с несколькими дополнительными комментариями:

from lmfit import minimize, Parameters, Parameter, report_fit
import numpy as np

xdata = np.array([177.,180.,183.,187.,189.,190.,196.,197.,201.,202.,203.,204.,206.,218.,225.,231.,234.,
      252.,262.,266.,267.,268.,277.,286.,303.])

ydata = np.array([0.81,0.74,0.78,0.75,0.77,0.81,0.73,0.76,0.71,0.74,0.81,0.71,0.74,0.71,
      0.72,0.69,0.75,0.59,0.61,0.63,0.64,0.63,0.35,0.27,0.26])

def fit_fc(params, x, data):

    n1 = params['n1'].value
    n2 = params['n2'].value
    n3 = params['n3'].value
    n4 = params['n4'].value
    n5 = params['n5'].value

    model = n1 + (n2 * x + n3) * 1./ (1. + np.exp(n4 * (n5 - x)))

    return model - data #that's what you want to minimize

# create a set of Parameters
# 'value' is the initial condition
# 'min' and 'max' define your boundaries
params = Parameters()
params.add('n1', value= 0.2, min=0.2, max=0.8)
params.add('n2', value= -0.005, min=-0.3, max=10**(-10))
params.add('n3', value= 1.0766, min=-1000., max=1000.)
params.add('n4', value= -0.36379, min=-1000., max=1000.)
params.add('n5', value= 274.0, min=0., max=1000.)

# do fit, here with leastsq model
result = minimize(fit_fc, params, args=(xdata, ydata))

# write error report
report_fit(params)

xplot = np.linspace(min(xdata), max(xdata), 1000)
yplot = result.values['n1'] + (result.values['n2'] * xplot + result.values['n3']) * \
                              1./ (1. + np.exp(result.values['n4'] * (result.values['n5'] - xplot)))
#plot results
try:
    import pylab
    pylab.plot(xdata, ydata, 'k+')
    pylab.plot(xplot, yplot, 'r')
    pylab.show()
except:
    pass

РЕДАКТИРОВАТЬ:

Если вы используете версию 0.9.x, вам необходимо соответствующим образом изменить код; проверьте здесь, какие изменения были внесены с 0.8.3 до 0.9.x.

Источник

Примечание: Новое в версии 0.17 SciPy

Предположим, вы хотите подогнать модель к данным, которая выглядит следующим образом:

y=a*t**alpha+b

и с ограничением на альфа

0<alpha<2

в то время как другие параметры a и b остаются свободными. Тогда мы должны использовать опцию bounds в optimize.curve_fit:

import numpy as np
from scipy.optimize import curve_fit
def func(t, a,alpha,b):
     return a*t**alpha+b
param_bounds=([-np.inf,0,-np.inf],[np.inf,2,np.inf])
popt, pcov = optimize.curve_fit(func, xdata,ydata,bounds=param_bounds)

Источник здесь

Источник

Попробуйте модуль lmfit ( http://lmfit.github.io/lmfit-py/). Он добавляет способ исправления или установки границ параметров для многих подпрограмм оптимизации в scipy.optimize, включая метод наименьших квадратов, и предоставляет множество инструментов, облегчающих подгонку.

Источник

Поскольку curve_fit() использует метод наименьших квадратов, вы можете посмотреть на scipy.optimize.fmin_slsqp(), что позволяет выполнять ограниченную оптимизацию. Проверьте это руководство о том, как его использовать.

Источник
Другие вопросы по тегам