Как вычислить дискретное преобразование Фурье?

Question

Я пытался найти несколько мест, чтобы помочь мне лучше понять DFT и как его вычислить, но безрезультатно. Поэтому мне нужна помощь в понимании DFT и вычислении комплексных чисел.

По сути, я просто ищу примеры того, как вычислить DFT с объяснением того, как он был вычислен, потому что, в конце концов, я хочу создать алгоритм для его вычисления.

Answer 1

Я предполагаю, 1D DFT/IDFT ...

Все DFT используют эту формулу:

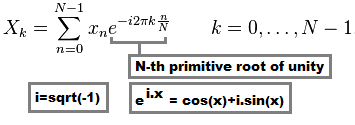
• X(k) преобразуется значение выборки (комплексный домен)
• x(n) значение выборки входных данных (реальная или сложная область)
• N количество образцов / значений в вашем наборе данных

Вся эта вещь обычно умножается на константу нормализации c, Как вы можете видеть для единственного значения, которое вам нужно N расчеты так для всех образцов это O(N^2) что медленно

Здесь мой Real<->Сложный домен DFT / IDFT в C++, вы также можете найти подсказки о том, как вычислить 2D-преобразование с 1D-преобразованием и как вычислить N-point DCT,IDCT по N-point DFT,IDFT там.

Быстрые алгоритмы

Существуют быстрые алгоритмы, основанные на разделении этого уравнения на нечетные и четные части суммы по отдельности (что дает 2x N/2 суммы), который также O(N) за одно значение, но 2 половинки являются одинаковыми уравнениями +/- какой-то постоянный твик. Таким образом, одна половина может быть вычислена непосредственно из первой. Это ведет к O(N/2) за одно значение. если вы примените это рекурсивно, то вы получите O(log(N)) за одно значение. Так что все стало O(N.log(N)) это здорово, но также добавляет следующие ограничения:

Все DFFT нуждаются во входном наборе данных, размер которого равен степени двух!!!

Так что это может быть рекурсивно разделено. Нулевое заполнение до ближайшей большей степени 2 используется для неверных размеров набора данных (в аудиотехнике иногда даже сдвиг фазы). Смотри сюда:

• Мой Комплекс-> Комплексный домен DFT,DFFT в C++
• некоторые советы по созданию FFT-подобных алгоритмов

Сложные числа

• c = a + i*b
• c комплексное число
• a это его реальная часть (Re)
• b это его мнимая часть (Im)
• i*i=-1 мнимая единица

так что вычисление так

дополнение:

c0+c1=(a0+i.b0)+(a1+i.b1)=(a0+a1)+i.(b0+b1)

умножение:

c0*c1=(a0+i.b0)*(a1+i.b1)
     =a0.a1+i.a0.b1+i.b0.a1+i.i.b0.b1
     =(a0.a1-b0.b1)+i.(a0.b1+b0.a1)

реальное -> сложное преобразование:

complex = real+i.0

[заметки]

• не забывайте, что вам нужно конвертировать данные в другой массив (не на месте)
• Константа нормализации на рекурсии БПФ сложна (обычно что-то вроде /=log2(N) зависит также от условия остановки рекурсии)
• не забудьте остановить рекурсию, если N=1 or 2...
• Остерегайтесь FPU может переполниться на больших наборах данных (N большой)
• здесь некоторые идеи для DFT/DFFT
• вот 2D БПФ и пример обтекания
• обычно формула Эйлера используется для вычисления e^(i.x)=cos(x)+i.sin(x)
• здесь Как получить частоты каждого значения в БПФ? Вы найдете, как получить частоты Niquist

Answer 2

Я читал " Руководство ученого и инженера по цифровой обработке сигналов" Стивена В. Смита. Это бесплатный PDF. В главе 12 он шаг за шагом рассматривает одну из реализаций БПФ (комплексное БПФ с вводом действительного числа) и представляет в конце RealFFT (который представляет собой БПФ, измененное специально для реальных входных данных). Есть еще одна глава, посвященная сложному БПФ. Книга немного старая, поэтому примеры программирования, написанные на BASIC и FORTRAN, кажутся древними, но концепции хорошо объяснены и проиллюстрированы.

Answer 3

Вот действительно хороший пример (IMHO): http://www.phpclasses.org/package/6193-PHP-Compute-the-Fast-Fourier-Transform-of-sampled-data.html

Это алгоритм БПФ, написанный на PHP, который также имеет сложное вычисление чисел. Может быть полезно в вашем случае.

Я нашел это невероятно полезным, когда я работал над своим проектом с отличием. Есть также несколько хороших ссылок, но в данный момент у меня их нет (меня сейчас нет дома).