Использование алгоритма FFT для расчета
Заданный набор из n частиц носителей электрического заряда находитс в точках (1,0), (2,0), .... (n,0) на плоскости. Заряд частицы, найденный в точке (i,0), обозначается как Qi. сила, действующая на частицу, определяется по формуле:
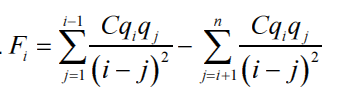 С - кулоновская константа.
С - кулоновская константа.
Приведите алгоритм вычисления Fi для всех частиц общей сложности O(nlgn). Подсказка: используйте алгоритм FFT.
Кажется, что Fi уже делится на четные и нечетные точки..
Я думал о том, чтобы разделить каждую сумму, чтобы вычислить БПФ (но делим до чего..?), А затем суммировать всегда половину баллов (потому что это и есть причина БПФ), а затем вычесть результат сумм, приведенных в формуле.,
есть идеи как сделать это лучше?
1 ответ
Похоже на домашнее задание, поэтому для вашего случая не приводится никакого реального кода, а приведен пример и подсказки.
для FFT- подобных алгоритмов:
установить размер набора данных в степень
2заполнением нулямипоэтому деление пополам просто (без остатка)
создать рекурсивную функцию для вычисления ваших FFT-подобных вещей
в нем переупорядочиваем набор данных, делим его на две половины и рекурсивно называем его self 2 раза (каждый со своей половиной данных) и добавляем оператор if для запуска. Если набор данных
size<=1или же2затем верните вычисленное значение, чтобы рекурсия остановилась.После этих двух рекурсивных вызовов переупорядочьте данные обратно и объедините их в результат.
удалить нулевой отступ из результата, если это необходимо
Например, вот так выглядит мой NTT (Теоретическое преобразование числа)
//---------------------------------------------------------------------------
void fourier_NTT:: NTT_fast(DWORD *dst,DWORD *src,DWORD n,DWORD w)
{
// recursion stop condition if the data is single number ...
if (n<=1) { if (n==1) dst[0]=src[0]; return; }
DWORD i,j,a0,a1,n2=n>>1,w2=modmul(w,w);
// reorder even,odd to dst array
for (i=0,j=0;i<n2;i++,j+=2) dst[i]=src[j];
for ( j=1;i<n ;i++,j+=2) dst[i]=src[j];
// recursion
NTT_fast(src ,dst ,n2,w2); // even
NTT_fast(src+n2,dst+n2,n2,w2); // odd
// restore results
for (w2=1,i=0,j=n2;i<n2;i++,j++,w2=modmul(w2,w))
{
a0=src[i];
a1=modmul(src[j],w2);
dst[i]=modadd(a0,a1);
dst[j]=modsub(a0,a1);
}
}
//---------------------------------------------------------------------------
Полный исходный код и дополнительная информация здесь.
Всегда сравнивайте результаты быстрой реализации с медленной реализацией!!!
Небольшая ошибка в каком-либо коэффициенте или индексе может привести к огромным различиям в результатах с ростом размера набора данных.
Это медленная реализация вышеупомянутой функции NTT:
//---------------------------------------------------------------------------
void fourier_NTT:: NTT_slow(DWORD *dst,DWORD *src,DWORD n,DWORD w)
{
DWORD i,j,wj,wi,a,n2=n>>1;
for (wj=1,j=0;j<n;j++)
{
a=0;
for (wi=1,i=0;i<n;i++)
{
a=modadd(a,modmul(wi,src[i]));
wi=modmul(wi,wj);
}
dst[j]=a;
wj=modmul(wj,w);
}
}
//---------------------------------------------------------------------------
[Заметки]
теперь у вас есть уравнение разделения
выведите разность коэффициентов между непосредственно вычисленным значением и значением, вычисленным с помощью 2x половинного рекурсивного вызова, и восстановите свой результат соответственно, чтобы выходные данные соответствовали правильному результату.