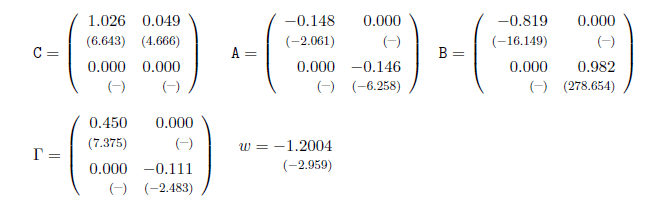Как использовать и интерпретировать двумерную модель GARCH GJR с помощью mGJR()
Я использую двумерную модель GJR с помощью команды mGJR() из R.
В инструкции из пакета "mgarchBEKK" сказано, что я ввожу первый временной ряд, второй временной ряд и так далее. Я пытаюсь использовать неожиданные результаты в качестве входных данных и мне нужны коэффициенты из них.
Я думал, что мне нужно было ввести мои заранее рассчитанные неожиданные результаты в качестве моего первого временного ряда, второго временного ряда и так далее в мою модель.
Тем не менее, когда я запускаю mGJR(), он выдает выходные данные, в которых говорится "$rema1" и "$rema2", которые выглядят как остатки (то есть неожиданные результаты), которые я искал.
Если да, то нужно ли вводить в модель результаты, а не неожиданные, чтобы автоматически получать неожиданные результаты?
Кроме того, как выглядит моя двумерная модель GJR GARCH, если я попытаюсь описать ее, используя коэффициенты, полученные из моего вывода ниже? Как я могу получить коэффициенты для модели, которые мне нужны для моего анализа из длинного вывода, который у меня есть ниже? В частности, я обнаружил, что у меня есть 17 коэффициентов, где один из них равен нулю. Я считаю, что эти коэффициенты сгруппированы по 4, где последний - только один слева.
Например, я нахожу $ est.params $1, $ est.params $2, $ est.params $3, $ est.params $4, $ est.params $5где в общей сложности 17 параметров. Однако я не уверен, насколько математически они выражены явно в формальной двумерной формуле GJR GARCH.
Обратите внимание, что это "двумерный" GJR GARCH, а не только GJR GARCH. Таким образом, у меня есть 17 параметров, в которых у меня есть 4 блока, каждый из которых имеет 4 коэффициента плюс один параметр, в результате чего получается всего 17. Однако я не знаю, какой параметр соответствует какому переменному коэффициенту. Я пытался предоставить как можно больше информации, но, если потребуется какое-либо разъяснение, пожалуйста, дайте мне знать.
Вывод, который я получаю, используя ожидаемый доход, следующий:
mGJR (eps1, eps2, order = c (1, 1, 1))
Warning: initial values for the parameters are set at:
2 0 2 0.4 0.1 0.1 0.4 0.4 0.1 0.1 0.4 0.1 0.1 0.1 0.1 0.5
Starting estimation process via loglikelihood function implemented in C.
Optimization Method is ' BFGS '
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
H IS SINGULAR!...
Estimation process completed.
Starting diagnostics...
Calculating estimated:
1. residuals,
2. correlations,
3. standard deviations,
4. eigenvalues.
Diagnostics ended...
Class attributes are ready via following names:
eps1 eps2 series.length estimation.time total.time order estimation aic asy.se.coef est.params cor sd1 sd2 H.estimated eigenvalues uncond.cov.matrix resid1 resid2
$eps1
[1] -0.002605971 0.110882333 -0.148960989 -0.068514869 -0.003755887
[6] 0.010796054 -0.147830267 0.047830346 0.028587561 0.003945359
[11] 0.082094667 -0.027768830 -0.006713995 0.024364330 -0.012109627
[16] -0.018345875 0.025668553 0.004490535 0.017510124 0.027143473
[21] 0.011606530 0.010522457 0.026053738 0.009380949 -0.070996648
[26] 0.020755072 -0.005830603 0.014289265 -0.000418889 0.022697292
[31] 0.023063329 0.005635615 0.049926161 0.013989454 0.019870327
[36] 0.018279627 0.014478743 -0.002177036 0.024635614 0.050726032
[41] -0.004392337 0.001234857 -0.018066777 -0.054437778 0.010428982
[46] -0.082777078 0.127812102 0.008940764 -0.001295593 0.060328122
[51] -0.009104799 -0.007204478 0.045631975 0.023096514 0.010598574
[56] 0.016541977 -0.011387952 -0.038157908 0.010327360 0.044342365
[61] 0.035077460 0.017492338 0.038596692 0.137205423 -0.004735584
[66] 0.104792896 0.036139814 -0.096482047 -0.000561027 -0.002632458
[71] 0.016177144 0.025230196 0.031753168 0.068971843 0.054021759
[76] 0.027263191 -0.025345373 0.033643409 -0.060322431 0.030377924
[81] -0.069716766 -0.089266804
$eps2
[1] -0.002889166 0.003033355 -0.002152031 0.003236581 0.003236581
[6] -0.001602802 0.004961099 -0.003176289 -0.000264979 -0.000264979
[11] -0.000264979 -0.001112752 0.004795299 0.004795299 0.005683859
[16] 0.007793699 0.001613168 -0.000354773 0.001350773 -0.000303199
[21] 0.009337753 0.009337753 0.001886769 -0.001791025 0.005869744
[26] 0.004795546 0.004795546 0.004509183 0.005226653 0.000383686
[31] 0.000207546 0.000207546 0.000207546 0.001570381 0.001669796
[36] 0.000549576 0.000549576 -0.001210093 0.014468461 -0.005345880
[41] 0.000130449 0.000130449 -0.001412638 -0.003304416 0.000117946
[46] 0.002145056 0.002145056 -0.002114632 0.005395410 -0.003153774
[51] 0.001888270 -0.001988031 0.000716514 -0.000331566 -0.000331566
[56] -0.000325350 -0.002882419 -0.006754058 -0.006754058 -0.001131800
[61] -0.017930260 0.002718202 0.006840023 0.006840023 0.002059632
[66] 0.003552300 0.003350965 -0.000126651 -0.000126651 -0.000126651
[71] -0.000990530 0.006430433 0.002933145 0.002933145 -0.002259438
[76] 0.001770744 0.000417412 0.004213458 0.004213458 0.004360485
[81] 0.002158630 -0.000686097
$series.length
[1] 82
$estimation.time
Time difference of 0.109386 secs
$total.time
Time difference of 0.1562669 secs
$order
GARCH component ARCH component HJR component
1 1 1
$estimation
$estimation$par
[1] -3.902944e-02 -2.045331e-05 -4.296356e-03 2.268312e-01 2.111034e+00
[6] 1.350601e-04 1.252329e-01 -3.143425e-01 -1.538355e-02 -5.587068e-03
[11] -1.628474e-04 4.224089e-01 1.025256e-01 -7.414033e-03 -4.869328e-01
[16] -1.102507e+00
$estimation$value
[1] -459.6969
$estimation$counts
function gradient
278 53
$estimation$convergence
[1] 0
$estimation$message
NULL
$estimation$hessian
[,1] [,2] [,3] [,4] [,5]
[1,] 77991.191735 -27033.70607 -1.895287e+03 -655.73521140 -6.727215e+01
[2,] -27033.706072 3337349.78552 -3.369295e+05 -371.07738150 -1.447052e+02
[3,] -1895.286899 -336929.51987 1.109169e+07 -122.26145691 -5.595868e+00
[4,] -655.735211 -371.07738 -1.222615e+02 18.61522485 -1.311354e-02
[5,] -67.272152 -144.70520 -5.595868e+00 -0.01311354 3.109780e-01
[6,] 20.487872 -18111.17773 3.525887e+03 -5.52437237 -8.751496e-02
[7,] -26.898108 -2073.43486 -2.975629e+03 -0.26691407 -3.916406e-01
[8,] 1477.726124 320.50607 -4.807709e+02 -9.98402142 -9.782072e-01
[9,] 9.388141 -27.62368 -5.331019e+01 -0.16106385 -1.537450e-02
[10,] -179.429796 49000.01743 2.023153e+04 7.66772695 1.378254e+00
[11,] 16.757240 -87.91362 2.360375e+03 0.23119576 7.084715e-02
[12,] -317.440585 -56.15303 3.710999e+01 6.57357184 -1.785094e-01
[13,] 3.793978 98.71583 -1.142264e+01 -0.22870343 1.543862e-02
[14,] -146.123961 -9829.15416 -5.196531e+02 -29.62565159 4.260863e-01
[15,] 18.082524 131.52060 3.398486e+03 0.33823287 3.212786e-02
[16,] 11.460530 -240.54059 6.706526e+02 0.32655416 -4.680544e-03
[,6] [,7] [,8] [,9] [,10]
[1,] 2.048787e+01 -26.8981081 1477.7261235 9.38814077 -179.429796
[2,] -1.811118e+04 -2073.4348620 320.5060742 -27.62367781 49000.017430
[3,] 3.525887e+03 -2975.6287124 -480.7709387 -53.31018730 20231.529905
[4,] -5.524372e+00 -0.2669141 -9.9840214 -0.16106385 7.667727
[5,] -8.751496e-02 -0.3916406 -0.9782072 -0.01537450 1.378254
[6,] 4.340038e+03 72.0221887 23.7403796 4.74321851 -479.279271
[7,] 7.202219e+01 22.5064989 -0.6280896 0.21674046 -44.382358
[8,] 2.374038e+01 -0.6280896 123.3928335 2.05555317 -53.354577
[9,] 4.743219e+00 0.2167405 2.0555532 20.53760214 53.165201
[10,] -4.792793e+02 -44.3823578 -53.3545766 53.16520102 17583.612011
[11,] -2.045612e+00 1.0454365 38.9154805 -823.29002882 -1763.407498
[12,] -1.488681e+01 -0.5717977 -6.3888226 -0.05658090 -21.965231
[13,] -4.554201e-01 -0.2556849 0.1795778 0.01041940 1.602574
[14,] 2.372186e+02 -13.7297349 13.5989185 -1.51829772 -127.664692
[15,] -1.372792e+01 -1.3537030 0.4896836 0.05291901 12.398407
[16,] -2.586931e+00 -0.1781386 0.1308570 0.05498165 -7.648387
[,11] [,12] [,13] [,14] [,15]
[1,] 1.675724e+01 -317.4405852 3.79397825 -146.1239612 18.08252377
[2,] -8.791362e+01 -56.1530304 98.71583141 -9829.1541554 131.52059520
[3,] 2.360375e+03 37.1099898 -11.42263544 -519.6531079 3398.48583556
[4,] 2.311958e-01 6.5735718 -0.22870343 -29.6256516 0.33823287
[5,] 7.084715e-02 -0.1785094 0.01543862 0.4260863 0.03212786
[6,] -2.045612e+00 -14.8868094 -0.45542005 237.2185632 -13.72791768
[7,] 1.045436e+00 -0.5717977 -0.25568491 -13.7297349 -1.35370300
[8,] 3.891548e+01 -6.3888226 0.17957777 13.5989185 0.48968359
[9,] -8.232900e+02 -0.0565809 0.01041940 -1.5182977 0.05291901
[10,] -1.763407e+03 -21.9652313 1.60257372 -127.6646916 12.39840658
[11,] 4.214986e+04 -0.0719787 0.06153061 -11.5769904 1.70462536
[12,] -7.197870e-02 18.7268970 -0.46324902 -16.1849665 1.23612627
[13,] 6.153061e-02 -0.4632490 0.12685032 1.2327783 -0.20692983
[14,] -1.157699e+01 -16.1849665 1.23277827 3180.7362850 -40.24439774
[15,] 1.704625e+00 1.2361263 -0.20692983 -40.2443977 9.65359055
[16,] -1.608423e-01 -0.4136609 0.07688678 13.4226923 0.70015741
[,16]
[1,] 1.146053e+01
[2,] -2.405406e+02
[3,] 6.706526e+02
[4,] 3.265542e-01
[5,] -4.680544e-03
[6,] -2.586931e+00
[7,] -1.781386e-01
[8,] 1.308570e-01
[9,] 5.498165e-02
[10,] -7.648387e+00
[11,] -1.608423e-01
[12,] -4.136609e-01
[13,] 7.688678e-02
[14,] 1.342269e+01
[15,] 7.001574e-01
[16,] 2.609256e+00
$aic
[1] -443.6969
$asy.se.coef
$asy.se.coef[[1]]
[,1] [,2]
[1,] 0.005951115 0.0006300630
[2,] 0.000000000 0.0003293308
$asy.se.coef[[2]]
[,1] [,2]
[1,] 0.3150396 0.01581263
[2,] 2.3065406 0.24110204
$asy.se.coef[[3]]
[,1] [,2]
[1,] 0.1049158 0.007811719
[2,] 0.4800751 0.010559776
$asy.se.coef[[4]]
[,1] [,2]
[1,] 0.2626887 0.01915952
[2,] 3.1255330 0.36661918
$asy.se.coef[[5]]
[1] 0.6559587
$est.params
$est.params$`1`
[,1] [,2]
[1,] -0.03902944 -2.045331e-05
[2,] 0.00000000 -4.296356e-03
$est.params$`2`
[,1] [,2]
[1,] 0.2268312 0.0001350601
[2,] 2.1110340 0.1252329455
$est.params$`3`
[,1] [,2]
[1,] -0.31434246 -0.0055870676
[2,] -0.01538355 -0.0001628474
$est.params$`4`
[,1] [,2]
[1,] 0.4224089 -0.007414033
[2,] 0.1025256 -0.486932758
$est.params$`5`
[1] -1.102507
$cor
[1] NA 0.031402656 0.058089044 -0.283965989 0.160141195
[6] 0.053237600 0.024081209 0.199587984 0.050169828 0.024045688
[11] 0.022017308 0.015292008 -0.015322752 0.070343728 0.060106129
[16] 0.104828553 0.165459125 0.030923632 0.022277698 0.026315363
[21] 0.020411283 0.102018250 0.102516847 0.035770620 0.024838651
[26] 0.274964544 0.063922572 0.067181338 0.051522997 0.051263760
[31] 0.023492076 0.022088161 0.021845645 0.021179838 0.028180317
[36] 0.028967267 0.023372747 0.022865880 0.020896186 0.180173786
[41] 0.034766653 0.022790880 0.021499773 -0.005938808 -0.137011386
[46] 0.029587448 0.062026969 0.053761176 0.036707465 0.054668898
[51] 0.009740057 0.040966003 0.012100219 0.024982728 0.021599599
[56] 0.021286712 0.020662963 -0.000403477 -0.118423344 0.080086394
[61] 0.017643159 0.287047099 0.043052577 0.095924672 0.129103089
[66] 0.052969944 0.066284046 0.055521350 -0.095508217 0.040009553
[71] 0.022822525 0.020620174 0.080723033 0.044702009 0.051760071
[76] 0.015962034 0.031439947 0.021103665 0.057557712 0.184430145
[81] 0.061929502 0.074235107
$sd1
[1] NA 0.04250885 0.05256355 0.08452372 0.05574627 0.04322082
[7] 0.04134005 0.07735273 0.04624463 0.04210977 0.04121545 0.04524121
[13] 0.04400240 0.04235476 0.04419338 0.04269033 0.04362228 0.04244062
[19] 0.04124873 0.04171567 0.04157849 0.04691775 0.04729332 0.04297800
[25] 0.04133609 0.05057450 0.04475342 0.04245633 0.04322428 0.04275222
[31] 0.04173813 0.04159489 0.04119978 0.04290491 0.04182107 0.04199520
[37] 0.04156416 0.04141240 0.04126752 0.05496396 0.04274670 0.04132509
[43] 0.04113889 0.04241273 0.05098749 0.04227554 0.05554117 0.05507267
[49] 0.04276771 0.04274602 0.04200447 0.04140829 0.04167090 0.04296412
[55] 0.04157519 0.04119998 0.04124952 0.04231602 0.04991076 0.04371888
[61] 0.04217155 0.05092909 0.04333244 0.04758239 0.06275051 0.04389357
[67] 0.05246204 0.04515198 0.06193409 0.04361523 0.04139218 0.04118088
[73] 0.04553376 0.04376651 0.04708736 0.04252185 0.04248968 0.04285559
[79] 0.04458945 0.04858689 0.04500212 0.05183762
$sd2
[1] NA 0.004482407 0.004338972 0.004809936 0.004467527 0.004585295
[7] 0.004308208 0.004536616 0.004338359 0.004304288 0.004302985 0.004303282
[13] 0.004368628 0.004897167 0.004391425 0.005115556 0.005729580 0.004312162
[19] 0.004303200 0.004308760 0.004302868 0.004976847 0.005020608 0.004316566
[25] 0.004309195 0.004939797 0.004398925 0.004894407 0.004397014 0.004840029
[31] 0.004303750 0.004303055 0.004302843 0.004303352 0.004311628 0.004312208
[37] 0.004303962 0.004303769 0.004340892 0.005536457 0.004364419 0.004303177
[43] 0.004302664 0.004381032 0.004754002 0.004305919 0.004331610 0.004329750
[49] 0.004315664 0.004919065 0.004322781 0.004392385 0.004419426 0.004305283
[55] 0.004303278 0.004302883 0.004302743 0.004548148 0.005589150 0.004407496
[61] 0.004305608 0.004895706 0.004332758 0.004476358 0.004463722 0.004425254
[67] 0.004349885 0.004344478 0.004371742 0.004310808 0.004304083 0.004304599
[73] 0.004475105 0.004333152 0.004333715 0.004314340 0.004313605 0.004303264
[79] 0.004365063 0.004618021 0.004372850 0.004343962
$H.estimated
, , 1
[,1] [,2]
[1,] 2.398788e-03 6.043323e-06
[2,] 6.043323e-06 1.742282e-05
, , 2
[,1] [,2]
[1,] 1.807002e-03 5.983524e-06
[2,] 5.983524e-06 2.009197e-05
, , 3
[,1] [,2]
[1,] 2.762927e-03 1.324847e-05
[2,] 1.324847e-05 1.882667e-05
, , 4
[,1] [,2]
[1,] 0.0071442584 -1.154474e-04
[2,] -0.0001154474 2.313548e-05
, , 5
[,1] [,2]
[1,] 3.107646e-03 3.988284e-05
[2,] 3.988284e-05 1.995880e-05
, , 6
[,1] [,2]
[1,] 1.868039e-03 1.055064e-05
[2,] 1.055064e-05 2.102493e-05
, , 7
[,1] [,2]
[1,] 1.709000e-03 4.288901e-06
[2,] 4.288901e-06 1.856066e-05
, , 8
[,1] [,2]
[1,] 5.983444e-03 7.003934e-05
[2,] 7.003934e-05 2.058089e-05
, , 9
[,1] [,2]
[1,] 2.138566e-03 1.006536e-05
[2,] 1.006536e-05 1.882135e-05
, , 10
[,1] [,2]
[1,] 1.773233e-03 4.358343e-06
[2,] 4.358343e-06 1.852689e-05
, , 11
[,1] [,2]
[1,] 1.698713e-03 3.904758e-06
[2,] 3.904758e-06 1.851568e-05
, , 12
[,1] [,2]
[1,] 2.046767e-03 2.977135e-06
[2,] 2.977135e-06 1.851824e-05
, , 13
[,1] [,2]
[1,] 1.936211e-03 -2.945494e-06
[2,] -2.945494e-06 1.908491e-05
, , 14
[,1] [,2]
[1,] 1.793925e-03 1.459058e-05
[2,] 1.459058e-05 2.398224e-05
, , 15
[,1] [,2]
[1,] 1.953055e-03 1.166491e-05
[2,] 1.166491e-05 1.928461e-05
, , 16
[,1] [,2]
[1,] 1.822465e-03 2.289296e-05
[2,] 2.289296e-05 2.616891e-05
, , 17
[,1] [,2]
[1,] 1.902904e-03 4.135442e-05
[2,] 4.135442e-05 3.282809e-05
, , 18
[,1] [,2]
[1,] 1.801206e-03 5.659359e-06
[2,] 5.659359e-06 1.859474e-05
, , 19
[,1] [,2]
[1,] 1.701457e-03 3.954325e-06
[2,] 3.954325e-06 1.851753e-05
, , 20
[,1] [,2]
[1,] 1.740197e-03 4.729997e-06
[2,] 4.729997e-06 1.856541e-05
, , 21
[,1] [,2]
[1,] 1.728771e-03 3.651716e-06
[2,] 3.651716e-06 1.851467e-05
, , 22
[,1] [,2]
[1,] 2.201275e-03 2.382151e-05
[2,] 2.382151e-05 2.476901e-05
, , 23
[,1] [,2]
[1,] 2.236658e-03 2.434172e-05
[2,] 2.434172e-05 2.520650e-05
, , 24
[,1] [,2]
[1,] 1.847108e-03 6.636071e-06
[2,] 6.636071e-06 1.863274e-05
, , 25
[,1] [,2]
[1,] 1.708672e-03 4.424391e-06
[2,] 4.424391e-06 1.856916e-05
, , 26
[,1] [,2]
[1,] 2.557780e-03 6.869377e-05
[2,] 6.869377e-05 2.440159e-05
, , 27
[,1] [,2]
[1,] 2.002868e-03 1.258424e-05
[2,] 1.258424e-05 1.935054e-05
, , 28
[,1] [,2]
[1,] 1.802540e-03 1.396019e-05
[2,] 1.396019e-05 2.395522e-05
, , 29
[,1] [,2]
[1,] 1.868338e-03 9.792344e-06
[2,] 9.792344e-06 1.933373e-05
, , 30
[,1] [,2]
[1,] 0.0018277521 1.060760e-05
[2,] 0.0000106076 2.342588e-05
, , 31
[,1] [,2]
[1,] 1.742072e-03 4.219893e-06
[2,] 4.219893e-06 1.852227e-05
, , 32
[,1] [,2]
[1,] 1.730135e-03 3.953452e-06
[2,] 3.953452e-06 1.851628e-05
, , 33
[,1] [,2]
[1,] 1.697422e-03 3.872712e-06
[2,] 3.872712e-06 1.851446e-05
, , 34
[,1] [,2]
[1,] 1.840831e-03 3.910538e-06
[2,] 3.910538e-06 1.851884e-05
, , 35
[,1] [,2]
[1,] 1.749002e-03 5.081388e-06
[2,] 5.081388e-06 1.859014e-05
, , 36
[,1] [,2]
[1,] 1.763597e-03 5.245741e-06
[2,] 5.245741e-06 1.859513e-05
, , 37
[,1] [,2]
[1,] 1.727580e-03 4.181164e-06
[2,] 4.181164e-06 1.852409e-05
, , 38
[,1] [,2]
[1,] 1.714987e-03 4.075372e-06
[2,] 4.075372e-06 1.852243e-05
, , 39
[,1] [,2]
[1,] 1.703008e-03 3.743298e-06
[2,] 3.743298e-06 1.884335e-05
, , 40
[,1] [,2]
[1,] 3.021037e-03 5.482789e-05
[2,] 5.482789e-05 3.065235e-05
, , 41
[,1] [,2]
[1,] 1.827281e-03 6.486224e-06
[2,] 6.486224e-06 1.904815e-05
, , 42
[,1] [,2]
[1,] 1.707763e-03 4.052884e-06
[2,] 4.052884e-06 1.851733e-05
, , 43
[,1] [,2]
[1,] 1.692408e-03 3.805606e-06
[2,] 3.805606e-06 1.851292e-05
, , 44
[,1] [,2]
[1,] 1.798840e-03 -1.103499e-06
[2,] -1.103499e-06 1.919344e-05
, , 45
[,1] [,2]
[1,] 2.599725e-03 -3.321083e-05
[2,] -3.321083e-05 2.260054e-05
, , 46
[,1] [,2]
[1,] 1.787221e-03 5.385952e-06
[2,] 5.385952e-06 1.854093e-05
, , 47
[,1] [,2]
[1,] 3.084822e-03 1.492262e-05
[2,] 1.492262e-05 1.876285e-05
, , 48
[,1] [,2]
[1,] 0.0030329985 1.281940e-05
[2,] 0.0000128194 1.874673e-05
, , 49
[,1] [,2]
[1,] 1.829077e-03 6.775136e-06
[2,] 6.775136e-06 1.862496e-05
, , 50
[,1] [,2]
[1,] 1.827222e-03 1.149525e-05
[2,] 1.149525e-05 2.419720e-05
, , 51
[,1] [,2]
[1,] 1.764375e-03 1.768562e-06
[2,] 1.768562e-06 1.868643e-05
, , 52
[,1] [,2]
[1,] 1.714646e-03 7.450944e-06
[2,] 7.450944e-06 1.929305e-05
, , 53
[,1] [,2]
[1,] 1.736464e-03 2.228394e-06
[2,] 2.228394e-06 1.953133e-05
, , 54
[,1] [,2]
[1,] 1.845916e-03 4.621122e-06
[2,] 4.621122e-06 1.853546e-05
, , 55
[,1] [,2]
[1,] 1.728496e-03 3.864375e-06
[2,] 3.864375e-06 1.851820e-05
, , 56
[,1] [,2]
[1,] 1.697438e-03 3.773681e-06
[2,] 3.773681e-06 1.851481e-05
, , 57
[,1] [,2]
[1,] 1.701523e-03 3.667388e-06
[2,] 3.667388e-06 1.851360e-05
, , 58
[,1] [,2]
[1,] 1.790646e-03 -7.765298e-08
[2,] -7.765298e-08 2.068565e-05
, , 59
[,1] [,2]
[1,] 2.491084e-03 -3.303522e-05
[2,] -3.303522e-05 3.123859e-05
, , 60
[,1] [,2]
[1,] 1.911341e-03 1.543191e-05
[2,] 1.543191e-05 1.942602e-05
, , 61
[,1] [,2]
[1,] 1.778439e-03 3.203542e-06
[2,] 3.203542e-06 1.853826e-05
, , 62
[,1] [,2]
[1,] 2.593772e-03 7.157055e-05
[2,] 7.157055e-05 2.396793e-05
, , 63
[,1] [,2]
[1,] 1.877700e-03 8.083078e-06
[2,] 8.083078e-06 1.877280e-05
, , 64
[,1] [,2]
[1,] 2.264084e-03 2.043155e-05
[2,] 2.043155e-05 2.003778e-05
, , 65
[,1] [,2]
[1,] 3.937627e-03 3.616188e-05
[2,] 3.616188e-05 1.992481e-05
, , 66
[,1] [,2]
[1,] 1.926645e-03 1.028889e-05
[2,] 1.028889e-05 1.958287e-05
, , 67
[,1] [,2]
[1,] 2.752265e-03 1.512627e-05
[2,] 1.512627e-05 1.892150e-05
, , 68
[,1] [,2]
[1,] 2.038701e-03 1.089117e-05
[2,] 1.089117e-05 1.887449e-05
, , 69
[,1] [,2]
[1,] 3.835832e-03 -2.585979e-05
[2,] -2.585979e-05 1.911213e-05
, , 70
[,1] [,2]
[1,] 1.902289e-03 7.522472e-06
[2,] 7.522472e-06 1.858307e-05
, , 71
[,1] [,2]
[1,] 1.713313e-03 4.065956e-06
[2,] 4.065956e-06 1.852513e-05
, , 72
[,1] [,2]
[1,] 1.695865e-03 3.655281e-06
[2,] 3.655281e-06 1.852958e-05
, , 73
[,1] [,2]
[1,] 0.0020733237 1.644880e-05
[2,] 0.0000164488 2.002657e-05
, , 74
[,1] [,2]
[1,] 0.0019155075 8.477600e-06
[2,] 0.0000084776 1.877621e-05
, , 75
[,1] [,2]
[1,] 2.217220e-03 1.056233e-05
[2,] 1.056233e-05 1.878109e-05
, , 76
[,1] [,2]
[1,] 1.808108e-03 2.928295e-06
[2,] 2.928295e-06 1.861353e-05
, , 77
[,1] [,2]
[1,] 1.805373e-03 5.762429e-06
[2,] 5.762429e-06 1.860719e-05
, , 78
[,1] [,2]
[1,] 1.836602e-03 3.891915e-06
[2,] 3.891915e-06 1.851808e-05
, , 79
[,1] [,2]
[1,] 1.988219e-03 1.120279e-05
[2,] 1.120279e-05 1.905377e-05
, , 80
[,1] [,2]
[1,] 2.360685e-03 4.138156e-05
[2,] 4.138156e-05 2.132612e-05
, , 81
[,1] [,2]
[1,] 2.025191e-03 1.218695e-05
[2,] 1.218695e-05 1.912182e-05
, , 82
[,1] [,2]
[1,] 2.687139e-03 1.671631e-05
[2,] 1.671631e-05 1.887001e-05
$eigenvalues
[1] 4.55569683 0.22879456 0.17683774 0.01426322
$uncond.cov.matrix
[,1] [,2]
[1,] 0.002266730 0.001058754
[2,] 0.001058754 0.014184073
$resid1
[1] 0.000000000 2.606658633 -2.832423405 -0.803429943 -0.076228015
[6] 0.251640690 -3.578761931 0.627605808 0.618572249 0.093834350
[11] 1.992057160 -0.613463505 -0.151066326 0.568366658 -0.281145635
[16] -0.447418119 0.584725959 0.106051164 0.423859148 0.650891694
[21] 0.275002848 0.206027474 0.547710301 0.219653206 -1.720836929
[26] 0.388360723 -0.136578900 0.330299607 -0.015356362 0.530624264
[31] 0.552493411 0.135394145 1.211759017 0.325365217 0.474140365
[36] 0.434967460 0.348083690 -0.051966703 0.590366618 0.941768811
[41] -0.102859959 0.029817748 -0.438515201 -1.283947967 0.205149728
[46] -1.959551678 2.299605523 0.164294634 -0.034506773 1.415352264
[51] -0.217156708 -0.172233261 1.094882761 0.537781247 0.255092253
[56] 0.401673126 -0.274777615 -0.901794851 0.192673354 1.016721711
[61] 0.838610788 0.331314439 0.884670384 2.873061672 -0.079539903
[66] 2.384117962 0.685180049 -2.137240072 -0.009247067 -0.060258875
[71] 0.391339172 0.609775354 0.692992830 1.573446856 1.149792694
[76] 0.640567944 -0.596838960 0.783185773 -1.358186376 0.611629203
[81] -1.552405453 -1.721844943
$resid2
[1] 0.00000000 0.60291683 -0.34446882 0.47408464 0.74401685 -0.36208567
[7] 1.22988753 -0.83357295 -0.08954723 -0.06362390 -0.10131479 -0.25004018
[13] 1.09566787 0.94523475 1.31164457 1.57234641 0.19804905 -0.08528340
[19] 0.30541107 -0.08591785 2.16540690 1.86518502 0.32642704 -0.42228251
[25] 1.40120757 0.90215659 1.09997892 0.90303309 1.19070375 0.05489337
[31] 0.03646646 0.04553108 0.02427045 0.35872374 0.37528677 0.11605970
[37] 0.12034527 -0.28015423 3.32249290 -1.13529670 0.03315067 0.02970541
[43] -0.31984221 -0.76117735 0.05094163 0.55098391 0.36347692 -0.49720367
[49] 1.25203911 -0.71138871 0.43875324 -0.44653544 0.15015921 -0.08924866
[55] -0.08205853 -0.08336948 -0.66487750 -1.48534156 -1.19469384 -0.33165737
[61] -4.17835758 0.48521539 1.54523260 1.28097851 0.47447031 0.68879762
[67] 0.72978029 0.07920992 -0.02991489 -0.02720370 -0.23827852 1.48272617
[73] 0.60612812 0.61341050 -0.57651419 0.40119127 0.11384865 0.96428797
[79] 1.03790954 0.85330306 0.58221097 -0.04007542
attr(,"class")
[1] "mGJR"
Я пытаюсь повторить следующую ситуацию:
Затем я пытаюсь получить вывод, как показано ниже:
1 ответ
Команда mGJR используется для оценки модели GARCH (Обобщенная авторегрессионная условная гетероскедастичность). Модели GARCH используются для моделирования волатильности временных рядов (чаще всего доходности активов). Это (и множество параметров) - это то, что вы можете получить из встроенного объекта GJR.
Если вы хотите узнать больше о моделях GARCH в сочетании с примерами на R, я могу порекомендовать следующие книги Р. Цея:
- Анализ финансовых временных рядов и
- Анализ многомерных временных рядов: с R и финансовыми приложениями
Нужно ли вводить результаты, а не неожиданные результаты в модель, чтобы получить неожиданные результаты автоматически?
Обычно вход для моделей GARCH находится в прошлых наблюдаемых доходах. (см., например, цитируемые выше книги или эту статью Р. Энгла, человека, который первоначально предложил модель ARCH)
Существуют некоторые тесты для определения наличия линейных зависимостей во временном ряду. Если они есть, их необходимо удалить с помощью средней модели (например, модели VARIMA). Примеры и различные случаи также в Цайс Анализ финансовых временных рядов. Полный процесс построения модели волатильности хорошо описан на стр. 133.
Коротко: Ваш eps1 а также eps2 должны быть эти (исправленные по средней модели) возвращаемые ряды.
Кроме того, как выглядит моя двумерная модель GJR GARCH, если я попытаюсь описать ее, используя коэффициенты, полученные из моего вывода ниже? Как я могу получить коэффициенты для модели, которые мне нужны для моего анализа из длинного вывода, который у меня есть ниже?
Требуется немного покопаться, но, глядя на публикацию Schmidbauer & Roesch (2008) и кодекс mgarchBEKK похоже, что спецификация mGJR - это то, что авторы Schmidbauer & Roesch называют двумерным асимметричным квадратичным GARCH (baqGARCH), который на странице 5 связанной публикации определяется как:
Параметры из подобранного объекта GJR представлены в порядке убывания: C, A, B, Gamma, w. как на странице 7 публикации (значения, выделенные меньшим шрифтом в скобках, являются t-значениями):
Вот воспроизводимый пример для подгонки mGJR и доступа к параметрам:
# packages
library(mgarchBEKK)
# generate heteroscedastic data
dat <- simulateBEKK(series.count = 2, T = 200, c(1,1))
returns1 <- dat$eps[[1]]
returns2 <- dat$eps[[2]]
# fit GJR to data
my_mGJR <- mGJR(eps1 = returns1, eps2 = returns2, order = c(1, 1, 1))
# extract parameters from GJR object
my_param <- my_mGJR$est.params
# assign names
names(my_param) = c('C', 'A', 'B', 'Gamma', 'w')
# access parameters
my_param
Возьмите, например, коэффициент-матрицу B, [1,] а также [2,] скажу вам, какой ряд, [,1] а также [,2] какой столбец матрицы вы смотрите. Вот упрощенное объяснение: поскольку у вас есть двумерная модель, диагональные элементы [1,][,1] а также [2,][,2] являются коэффициентами, которые говорят вам что-то о соответствующей серии на его собственной дисперсии. Недиагональные элементы больше относятся к условной ковариации или вторичному влиянию двух серий.
Коротко: У вас есть уравнение из (2) -> Вы вводите коэффициенты, как показано выше -> Вы можете решить для H_T (условная ковариационная матрица в момент времени T) для переменных, зависящих от времени (returnseries_T-1, H_T-1).
В частности, я обнаружил, что у меня есть 17 коэффициентов, где один из них равен нулю.
Если коэффициент установлен на ноль, он не считается параметром. Недиагональный нижний коэффициент C всегда устанавливается на ноль. Таким образом, у вас есть 16 параметров (если вы не ограничиваете модель, как это сделали авторы в своей статье).
Тем не менее, когда я запускаю mGJR(), он выдает выходные данные, в которых говорится "$rema1" и "$ остаток2", которые выглядят как остатки
Это верно, они являются невязками, которые объясняются не коэффициентами, а условной волатильностью (не уверен, что вы говорите о "неожиданных доходах"). Это, так сказать, то, что нельзя объяснить моделью, случайным белым шумом (см., Например, здесь или википедию). Остатки в моделях GARCH в основном используются для выполнения некоторых тестов адекватности модели, чтобы ответить на вопрос: "Достаточно ли адекватно объясняется моя уравнение условной дисперсии в моей подобранной модели?"
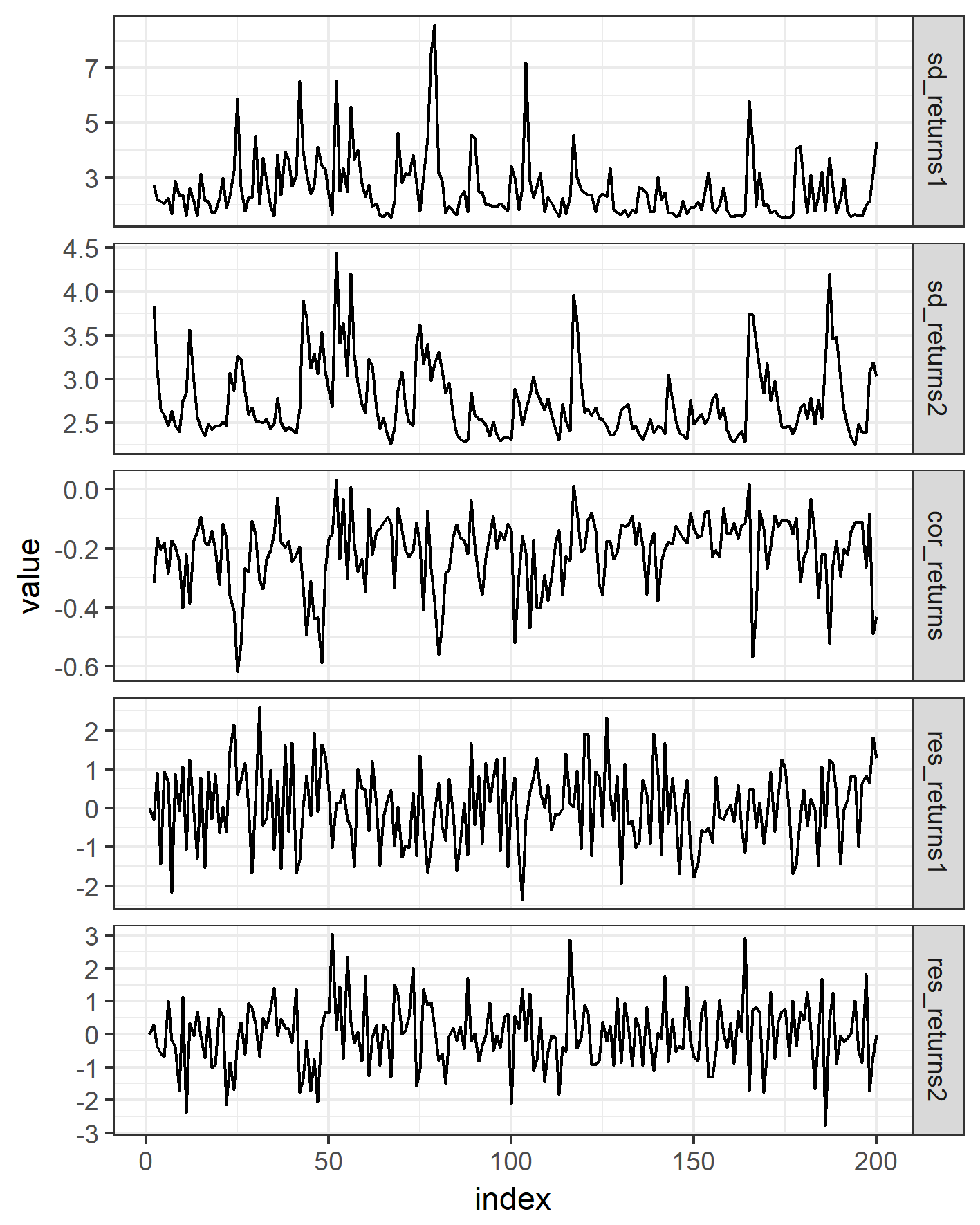
Здесь график условной волатильности, условной корреляции и остатков. Кажется, что есть некоторая кластеризация волатильности в условном отклонении ряда (первые два графика). Кажется, что в остаточной серии не так много структуры (последние два графика).
И код для сюжета:
library(ggplot2)
library(reshape2)
my_results <- data.frame(index = 1:200,
sd_returns1 = my_mGJR$sd1,
sd_returns2 = my_mGJR$sd2,
cor_returns = my_mGJR$cor,
res_returns1 = my_mGJR$resid1,
res_returns2 = my_mGJR$resid2)
# melt data to long format for plotting
p_results = melt(my_results, id = 'index')
# plot the results
my_p = ggplot(p_results, aes(x = index, y = value)) +
geom_line() +
facet_grid(variable ~ ., scales = "free_y") +
theme_bw()
ggsave('example_cor_sd_res.png', plot = my_p, device = 'png', units = 'cm',
width = 12, height = 15)
Я пытаюсь повторить следующую ситуацию:
В основном у вас есть все, что вам нужно. Значимость параметров (либо p-значений, либо t-значений) может быть рассчитана из стандартных ошибок параметров. Для t-значений, например, вам нужно разделить параметры на стандартные ошибки. Стандартные ошибки могут быть взяты из объекта GJR как:
my_param_se = my_mGJR$asy.se.coef
names(my_param_se) = paste0(rep("tvals_", 5), c('C', 'A', 'B', 'Gamma', 'w'))
my_param_se
Так как mGJR Модель команд (или baqGARCH) строится аналогично, например, BEKK-GARCH, которую вы, вероятно, не сможете интерпретировать так же, как в вашем примере. Как я уже говорил выше, диагональные элементы различных коэффициентов расскажут вам о значительной условной волатильности серии 1 из нововведений в серии 1. Недиагональные элементы расскажут вам кое-что о распространении волатильности из одной серии в другую. Если вы хотите учесть это, вам нужно будет включить эти результаты в свою таблицу.
Затем я пытаюсь получить вывод, как показано ниже:
Большую часть этого я объяснил выше, только одно примечание к остаткам. Похоже, адекватность модели была измерена с помощью теста LjungBox (=LB?). Смотрите, например, здесь.
Я надеюсь, что это отвечает на ваши вопросы.
Изменить: обновленный ответ, чтобы включить дополнительные вопросы.