Зачем использовать алгоритм Дейкстры, если поиск в ширину (BFS) может сделать то же самое быстрее?

Оба могут быть использованы для поиска кратчайшего пути из одного источника. BFS работает в O(E+V)в то время как Дейкстра бежит в O((V+E)*log(V)),

Кроме того, я видел, как Дейкстра часто использовал протоколы маршрутизации.

Итак, зачем использовать алгоритм Дейкстры, если BFS может делать то же самое быстрее?

Источник

7 ответов

Решение

Дейкстра позволяет назначать расстояния, отличные от 1, для каждого шага. Например, при маршрутизации расстояния (или веса) могут быть назначены по скорости, стоимости, предпочтениям и т. Д. Алгоритм затем дает вам кратчайший путь от вашего источника до каждого узла в пройденном графике.

Между тем BFS в основном просто расширяет поиск на один "шаг" (ссылка, ребро, как бы вы это ни называли в своем приложении) на каждой итерации, что приводит к поиску наименьшего числа шагов, необходимых для достижения любого данный узел из вашего источника ("корень").

Источник

Если вы рассматриваете туристические сайты, они используют алгоритм Дейкстры из-за весов (расстояний) на узлах.

Если вы будете учитывать одинаковое расстояние между всеми узлами, то BFS - лучший выбор.

Например, рассмотрим A -> (B, C) -> (F) с весом ребер, заданным A->B = 10, A->C = 20, B->F знак равно C->F = 5

Здесь, если мы применим BFS, ответ будет ABF или ACF, так как оба являются кратчайшими путями (по отношению к числу ребер), но если мы применим Dijstra's, ответ будет ABF только потому, что он учитывает веса на подключенном дорожка.

Источник

Алгоритм Дейкстры

  • Как BFS для взвешенных графиков.
  • Если все затраты равны, Dijkstra = BFS

Источник: https://cs.stanford.edu/people/abisee/gs.pdf

Источник

С точки зрения реализации, алгоритм Дейкстры может быть реализован точно так же, как BFS путем замены queue с priority queue,

Источник: введите описание ссылки здесь

Источник

Существует путаница по этому поводу, можно использовать модифицированный алгоритм BFS для поиска кратчайшего пути во взвешенном ориентированном графе:

  1. Использовать приоритетную очередь вместо обычной очереди
  2. Не отслеживать посещенные узлы, а вместо этого отслеживать расстояние от начального узла

Из-за 2 некоторые узлы будут посещаться более одного раза, что делает его менее эффективным по сравнению с Дейкстрой.

      shortest = sys.maxsize

queue = [(0, src, 0)]
while queue:
    (cost, node, hops) = heapq.heappop(queue)
    if node == dst:
        shortest = min(distance, cheapest)
    for (node_to, node_distance) in edges[node]:
        heapq.heappush(queue, (cost + node_distance, node_to, hops + 1))
Источник

И BFS, и Dijkstra можно использовать для поиска кратчайшего пути. Разница в том, как определяется кратчайший путь:

  • BFS: путь с наименьшим количеством ребер (при одинаковом весе для каждого ребра или без веса).
  • Дейкстра: путь с наименьшим весом на пути.

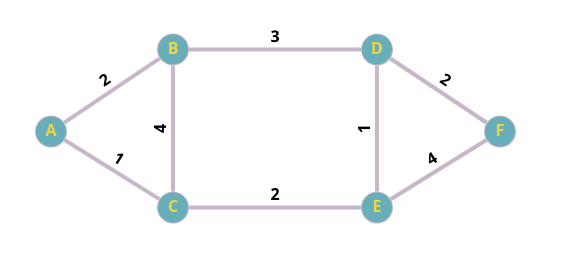
Рассмотрим этот неориентированный связный граф:

Мы хотим найти кратчайший путь изAкF:

  • BFS: A->C->E->F или A->B->D->F
  • Дейкстра: A->C->E->D->F

Реализация очень похожа, ключевой частью Dijkstra является использование приоритетной очереди. Я использовал Python для демонстрации:

          graph = {
        'A': {('B', 2), ('C', 1)},
        'B': {('A', 2), ('C', 4), ('D', 3)},
        'C': {('A', 1), ('B', 4), ('E', 2)},
        'E': {('C', 2), ('D', 1), ('F', 4)},
        'D': {('B', 3), ('E', 1), ('F', 2)},
        'F': {('D', 2), ('E', 4)}
    
    }
    
    
    def dijkstra(graph, start: str):
        result_map = defaultdict(lambda: float('inf'))
        result_map[start] = 0
    
        visited = set()
    
        queue = [(0, start)]
    
        while queue:
            weight, v = heapq.heappop(queue)
            visited.add(v)
    
            for u, w in graph[v]:
                if u not in visited:
                    result_map[u] = min(w + weight, result_map[u])
                    heapq.heappush(queue, [w + weight, u])
    
        return dict(result_map)
    
    print(dijkstra(graph, 'A'))

Выход:

      {'A': 0, 'C': 1, 'B': 2, 'E': 3, 'D': 4, 'F': 6}

В то время как для BFS достаточно обычной очереди:

          graph = {
        'A': {'B', 'C'},
        'B': {'A', 'C', 'D'},
        'C': {'A', 'B', 'E'},
        'E': {'C', 'D', 'F'},
        'D': {'B', 'E', 'F'},
        'F': {'D', 'E'}
    }
    
    
    def bfs(graph, start: str):
        result_map = defaultdict(int)
    
        visited = set()
        queue = deque([[start, 0]])
    
        while queue:
            v, depth = queue.popleft()
            visited.add(v)
    
            if v in graph:
                result_map[v] = depth
    
            for u in graph[v]:
                if u not in visited:
                    queue.append([u, depth + 1])
                    visited.add(u)
    
        return dict(result_map)
    
    
    print(bfs(graph, 'A'))

Выход:

      {'A': 0, 'C': 1, 'B': 1, 'E': 2, 'D': 2, 'F': 3}
Источник
  • BFS работает только в том случае, если вы считаете кратчайший путь числом ребер шагов или какое-либо другое приложение присваивает одинаковые (но положительные) веса всем ребрам.
  • Разница между BFS и Dijkstra заключается лишь в замене очереди FIFO очередью с приоритетом!

Обратите внимание, что это не исправляет ограничение положительных весов на ребрах, известный недостаток Дейкстры (и BFS), который исправлен Беллманом-Фордом путем уплаты штрафа за скорость.

Источник: главы 8.4, 8.6 в Erickson, Jeff (2019). Алгоритмы

Источник
Другие вопросы по тегам