Значения для моделирования хаотического рассеяния не совпадают с базовым случаем
Мой первый пост о переполнении стека, будьте осторожны. Я написал код для отслеживания положения на плоскости x,y частицы массы M на потенциале V(r), описываемой четырехмерной системой уравнений движения
M(dv/dt)=-grad V(r), dr/dt=v,
Которые решаются с помощью метода 4-го порядка Рунге Кутты, где r=(x,y) и v=(vx,vy); теперь состояние частицы определяется x,y и углом тета между вектором v и положительной осью x, где величина скорости определяется как
|v|=sqrt(2(E-V(r))/M)
где E - энергия в плоскости, а потенциал V(r) определяется как
V(r)=x^2y^2exp[-(x^2+y^2)],
теперь вот код, который я сделал для начальных значений
x(0)=3,
y(0)=0.3905,
vx(0)=0,
vy(0)=-sqrt(2*(E-V(x(0), y(0)))),
где E=0,260*(1/exp(2))
// RK4
#include <iostream>
#include <cmath>
// constant global variables
const double M = 1.0;
const double DeltaT = 1.0;
// function declaration
double f0(double t, double y0, double y1, double y2, double y3); // derivative of y0
double f1(double t, double y0, double y1, double y2, double y3); // derivative of y1
double f2(double t, double y0, double y1, double y2, double y3); // derivative of y2
double f3(double t, double y0, double y1, double y2, double y3); // derivative of y3
void rk4(double t, double h, double &y0, double &y1, double &y2, double &y3); // method of runge kutta 4th order
double f(double y0, double y1); //function to use
int main(void)
{
double y0, y1, y2, y3, time, E, Em;
Em = (1.0/(exp(2.0)));
E = 0.260*Em;
y0 = 3.0; //x
y1 = 0.3905; //y
y2 = 0.0; //vx
y3 = -(std::sqrt((2.0*(E-f(3.0, 0.0)))/M)); //vy
for(time = 0.0; time <= 400.0; time += DeltaT)
{
std::cout << time << "\t\t" << y0 << "\t\t" << y1 << "\t\t" << y2 << "\t\t" << y3 << std::endl;
rk4(time, DeltaT, y0, y1, y2, y3);
}
return 0;
}
double f(double y0, double y1)
{
return y0*y0*y1*y1*(exp(-(y0*y0)-(y1*y1)));
}
double f0(double t, double y0, double y1, double y2, double y3)
{
return y2;
}
double f1(double t, double y0, double y1, double y2, double y3)
{
return y3;
}
double f2(double t, double y0, double y1, double y2, double y3)
{
return 2*y0*((y0*y0)-1)*(y1*y1)*(exp(-(y0*y0)-(y1*y1)))/M;
}
double f3(double t, double y0, double y1, double y2, double y3)
{
return 2*(y0*y0)*y1*((y1*y1)-1)*(exp(-(y0*y0)-(y1*y1)))/M;
}
void rk4(double t, double h, double &y0, double &y1, double &y2, double &y3) // method of runge kutta 4th order
{
double k10, k11, k12, k13, k20, k21, k22, k23, k30, k31, k32, k33, k40, k41, k42, k43;
k10 = h*f0(t, y0, y1, y2, y3);
k11 = h*f1(t, y0, y1, y2, y3);
k12 = h*f2(t, y0, y1, y2, y3);
k13 = h*f3(t, y0, y1, y2, y3);
k20 = h*f0(t+h/2, y0 + k10/2, y1 + k11/2, y2 + k12/2, y3 + k13/2);
k21 = h*f1(t+h/2, y0 + k10/2, y1 + k11/2, y2 + k12/2, y3 + k13/2);
k22 = h*f2(t+h/2, y0 + k10/2, y1 + k11/2, y2 + k12/2, y3 + k13/2);
k23 = h*f3(t+h/2, y0 + k10/2, y1 + k11/2, y2 + k12/2, y3 + k13/2);
k30 = h*f0(t+h/2, y0 + k20/2, y1 + k21/2, y2 + k22/2, y3 + k23/2);
k31 = h*f1(t+h/2, y0 + k20/2, y1 + k21/2, y2 + k22/2, y3 + k23/2);
k32 = h*f2(t+h/2, y0 + k20/2, y1 + k21/2, y2 + k22/2, y3 + k23/2);
k33 = h*f3(t+h/2, y0 + k20/2, y1 + k21/2, y2 + k22/2, y3 + k23/2);
k40 = h*f0(t + h, y0 + k30, y1 + k31, y2 + k32, y3 + k33);
k41 = h*f1(t + h, y0 + k30, y1 + k31, y2 + k32, y3 + k33);
k42 = h*f2(t + h, y0 + k30, y1 + k31, y2 + k32, y3 + k33);
k43 = h*f3(t + h, y0 + k30, y1 + k31, y2 + k32, y3 + k33);
y0 = y0 + (1.0/6.0)*(k10 + 2*k20 + 2*k30 + k40);
y1 = y1 + (1.0/6.0)*(k11 + 2*k21 + 2*k31 + k41);
y2 = y2 + (1.0/6.0)*(k12 + 2*k22 + 2*k32 + k42);
y3 = y3 + (1.0/6.0)*(k13 + 2*k23 + 2*k33 + k43);
}
Проблема здесь в том, что когда я запускаю код с заданными начальными условиями, значения не совпадают с тем, что предполагается в соответствии с ситуацией, указанной в задаче.
как должна выглядеть графика с заданными начальными условиями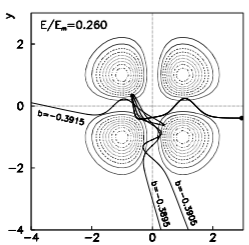
теперь, я думаю, что я правильно понял реализацию метода, но я не знаю, почему графики не совпадают, потому что когда я запускаю код, частица уходит от потенциала.
Любая помощь будет оценена.
1 ответ
Дорожки выглядят хаотично с резкими поворотами. Это требует адаптивного размера шага, вам нужно будет реализовать некоторый контроль размера шага. Либо сравнивая каждый шаг с двумя шагами по половине длины шага, либо используя метод со встроенными методами более высокого порядка, такими как Fehlberg или Dormand-Price.
Более непосредственные ошибки:
- определять
EmкакV(1,1)чтобы избежать ненужных магических чисел Ваша начальная позиция, если вы правильно прочитали график,
y0 = 3.0; y1 = -0.3905+k*0.0010;с
k=-1,0,1, обратите внимание на знак минус.Ваша начальная скорость горизонтальна, и кинетическая энергия вычисляется, чтобы дополнить потенциальную энергию в этой позиции. таким образом
y2 = v0 = -(std::sqrt((2.0*(E-V(y0, y1)))/M)); y3 = v1 = 0.0;
С этими изменениями и адаптивным решателем я получаю (в python) сюжет
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
# capture the structure of the potential
f = lambda r : r*np.exp(-r);
df = lambda r : (1-r)*np.exp(-r);
V = lambda y1,y2 : f(y1*y1)*f(y2*y2);
M= 1.0
Em = V(1.0,1.0);
E = 0.260*Em;
def prime(t,y):
x1,x2,v1,v2 = y
dV_dx1 = 2*x1*df(x1*x1)*f(x2*x2);
dV_dx2 = 2*x2*df(x2*x2)*f(x1*x1);
return [ v1, v2, -dV_dx1/M, -dV_dx2/M ];
# prepare and draw the contour plot
X1,X0=np.ogrid[-4:3:100j,-4:3:100j]
plt.contour(X0.ravel(), X1.ravel(), V(X0,X1), Em*np.arange(0,1,0.1), colors='k', linewidths=0.3)
# display grid and fix the coordinate ranges
plt.grid();plt.autoscale(False)
for k in range(-1,1+1):
x01 = 3.0;
x02 = b = -0.3905 + 0.0010*k;
v01 = -( ( E-V(x01,x02) )*2.0/M )**0.5;
v02 = 0.0;
print "initial position (%.4f, %.4f), initial velocity (%.4f, %.4f)" % ( x01, x02, v01, v02 )
t0 = 0.0
tf = 50.0
tol = 1e-10
y0 = [ x01, x02, v01, v02 ]
t = np.linspace(t0,tf,501); y = odeint(lambda y,t: prime(t,y) , y0, t)
plt.plot(y[:,0], y[:,1], label="b=%.4f" % b, linewidth=2)
plt.legend(loc='best')
plt.show()
