Различия в категориальных и порядковых признаках в регрессионном анализе?
Я пытаюсь полностью понять разницу между категориальными и порядковыми данными при проведении регрессионного анализа. Пока что понятно:
Категориальная особенность и пример данных:
Цвет: красный, белый, черный
Почему категорично: red < white < black логически неверно
Порядковая особенность и пример данных:
Состояние: старое, с ремонтом, новое
Почему порядковый: old < renovated < new логически правильно
Категориально-числовые и порядково-числовые методы кодирования:
One-Hot кодирование для категориальных данных
Произвольные числа для порядковых данных
Пример для категориального:
data = {'color': ['blue', 'green', 'green', 'red']}
Числовой формат после кодирования One-Hot:
color_blue color_green color_red
0 1 0 0
1 0 1 0
2 0 1 0
3 0 0 1
Пример для порядкового номера:
data = {'con': ['old', 'new', 'new', 'renovated']}
Числовой формат после использования сопоставления: Старый <обновленный <новый → 0, 1, 2
0 0
1 2
2 2
3 1
По моим данным цена увеличивается по мере того, как состояние меняется со "старого" на "новое". "Старый" в цифре был закодирован как "0". "Новый" в числовом формате был закодирован как "2". Таким образом, когда состояние увеличивается, цена также увеличивается. Правильный.
Теперь давайте посмотрим на функцию "цвет". В моем случае разные цвета также влияют на цену. Например, "черный" будет дороже, чем "белый". Но из вышеупомянутого числового представления категориальных данных я не вижу возрастающей зависимости, как это было с функцией "условие". Означает ли это, что изменение цвета не влияет на цену в регрессионной модели, если используется однократное кодирование? Зачем использовать однократное кодирование для регрессии, если оно никак не влияет на цену? Вы можете это уточнить?
ОБНОВЛЕНИЕ К ВОПРОСУ:
Сначала я ввожу формулу для линейной регрессии: 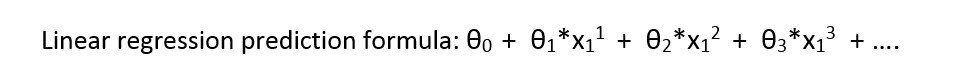
Давайте посмотрим на представления данных для цвета: 
2 ответа
Вы увидите не увеличивающуюся зависимость. Весь смысл этой дискриминации в том, что цвет - это не та особенность, которую вы можете осмысленно поместить в континуум, как вы уже отметили.
Однократное кодирование делает программное обеспечение очень удобным для анализа этого измерения. Вместо того, чтобы иметь функцию "цвет" с перечисленными значениями, у вас есть набор логических (присутствующих / не присутствующих) функций. Например, ваша строка 0 выше имеет функции color_blue = true, color_green = false и color_red = false.
Данные прогноза, которые вы получаете, должны показывать каждый из них как отдельное измерение. Например, присутствие color_blue может стоить 200 долларов, а зеленый - 100 долларов.
Резюме: не ищите линию линейной регрессии, проходящую через (несуществующую) цветовую ось; скорее ищите факторы color_*, по одному для каждого цвета. Что касается алгоритма анализа, это совершенно независимые функции; "горячее" кодирование (термин от конструкции цифровой схемы) - это просто наше соглашение для решения этой проблемы.
Помогает ли это вашему пониманию?
После редактирования вопроса 02:03 Z 04.12.2015:
Нет, ваше предположение неверно: эти два представления не просто вопрос удобства. Упорядочение цветов работает для этого примера - потому что эффект оказывается аккуратной, линейной функцией выбранного кодирования. Как показывает ваш пример, ваша более простая кодировка предполагает, что цены от белого к красному к черному являются линейным прогрессом. Что вы делаете, когда зеленый, синий и коричневый все стоят по 25 долларов, редкий желтый стоит 500 долларов, а прозрачный снижает цену на 1000 долларов?
Кроме того, как вы узнали заранее, что черные стоят больше, чем белые, в свою очередь, стоят больше, чем красные?
Рассмотрим случай с ценами на жилье, основанными на округе начальной школы, с 50 районами в области. Если вы используете числовое кодирование - номер школьного округа, порядковый номер в алфавитном порядке или какой-либо другой произвольный порядок - регрессионному программному обеспечению будет очень трудно найти корреляцию между этим числом и ценой на жилье. PS 107 более дорогой район, чем PS 32 или PS 15? Аддингтон и Бендемир предпочитают Юнион-Сити и Вентура?
Разделение их на 50 различных функций по такому горячему принципу отделяет функцию от кодирования и позволяет программному обеспечению для анализа обрабатывать их математически значимым образом. Он не идеален ни в коем случае - расширение, скажем, с 20 функций до 70 означает, что для сближения потребуется больше времени - но мы действительно получаем значимые результаты для школьного округа.
При желании вы можете теперь закодировать эту функцию в ожидаемом порядке значений и получить разумное соответствие с небольшой потерей точности и более быстрым прогнозированием из вашей модели (меньше переменных).
Вы не можете использовать порядковый код для категориальной переменной, где порядок не имеет значения. Основная цель построения регрессионной модели состоит в том, чтобы увидеть, насколько изменение одной переменной влияет на переменную отклика. Когда вы получаете формулу регрессии, вот как вы ее читаете: "1 единица изменения в переменной X вызывает theta_x изменение переменной ответа ".
Например, допустим, вы построили регрессионную модель цен на жилье и получили это: price = 1000 + (-50)*age_of_house, Это означает, что увеличение возраста дома на 1 год приводит к снижению цены на 50.
Если у вас есть категориальная переменная, вы не можете упомянуть изменение единицы в этой переменной. Вы не можете сказать, на 1 единицу увеличение / уменьшение цвета... и т. Д. Итак, горячее кодирование, как Prune сказано в его / ее ответе, это просто соглашение для работы с категориальными переменными. Это позволяет вам интерпретировать результаты, например, если дом белого цвета, он добавляет 200 долларов к значению, когда коэффициент color_white в вашей окончательной модели равен +200. Если дом не белый, эта переменная не влияет на вашу переменную ответа, потому что значение будет 0.
Не забывайте, что модели "линейной регрессии" могут объяснить только линейные отношения между переменными.
Надеюсь, это поможет.