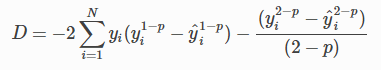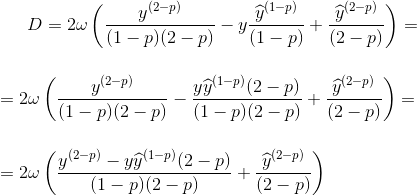Формула среднего остаточного отклонения в H2O

Question

Я пытаюсь выяснить точную формулу, используемую в H2O для функции потери среднего остаточного отклонения для распределения Твиди.

Или вообще, каково будет среднее остаточное отклонение для распределенной зависимой переменной Твиди?

До сих пор я нашел эту страницу ( http://docs.h2o.ai/h2o/latest-stable/h2o-docs/data-science/glm.html), где формула отклонения для распределения твиди дается как:

Однако внутри кода H2O, найденного на github в строке 103 этой страницы ( https://github.com/h2oai/h2o-3/blob/master/h2o-core/src/main/java/hex/Distribution.java#L103) формула указана по-разному (без учета омега, которая является просто весом, и отсутствие суммирования):

2 * w * (Math.pow(y, 2 - tweediePower) / ((1 - tweediePower) * (2 - tweediePower)) - y * exp(f * (1 - tweediePower)) / (1 - tweediePower) + exp(f * (2 - tweediePower)) / (2 - tweediePower))

который в форме уравнения:

Итак, документация неправильная или реализация? Буду признателен за любую помощь!

Спасибо!

Answer 1

Спасибо за указание на это, в то время как уравнение бэкэнда, расположенное здесь, является правильным (поэтому реализация верна), уравнение в документации кажется неправильным. Я создал этот билет Jira, чтобы обновить уравнение в документации. Билет содержит правильное уравнение вместе с полезной информацией для его получения.