Как использовать TetGen для этой простой трехмерной геометрии

Question

Вот точки, определяющие мою простую трехмерную геометрию.

datN = {{{-0.47150460764747554`, 0.29559274991660417`, 
 0.010131794240974218`}, {-0.4762714873728534`, 
 0.2955927499166042`, 
 0.010567957416020535`}, {-0.4835042628911566`, 
 0.29559274991660417`, 
 0.01066658601048008`}, {-0.49133736140975415`, 
 0.29559274991660417`, 
 0.01010572204377315`}, {-0.4974365622729896`, 
 0.29559274991660417`, 
 0.009602808597554033`}, {-0.4999590574180981`, 
 0.2955927499166041`, 
 0.010150149141898643`}, {-0.497870343592127`, 
 0.2955927499166042`, 
 0.011728012221066566`}, {-0.491634397829927`, 
 0.2955927499166041`, 
 0.013089897457762985`}, {-0.4834169387190052`, 
 0.2955927499166042`, 
 0.013009607974106477`}, {-0.47609963350102275`, 
 0.2955927499166043`, 
 0.011622413291940486`}, {-0.471504606936728`, 
 0.2955927499166041`, 
 0.010131794240974216`}}, {{-0.5619323339485054`, 
 0.13709660728856332`, 
 0.010131794240974218`}, {-0.5878076066290028`, 
 0.13709660728856335`, 
 0.01249934738636439`}, {-0.6270680976744502`, 
 0.13709660728856332`, 
 0.0130347168361427`}, {-0.6695872237650179`, 
 0.13709660728856332`, 
 0.00999027080199048`}, {-0.7026945171227986`, 
 0.13709660728856332`, 
 0.007260388089336815`}, {-0.7163869644835803`, 
 0.13709660728856332`, 
 0.010231427144215837`}, {-0.705049141229765`, 
 0.13709660728856338`, 
 0.018796282936276536`}, {-0.6711995779276564`, 
 0.13709660728856332`, 
 0.02618878157043711`}, {-0.6265940901692914`, 
 0.13709660728856332`, 
 0.02575295931296998`}, {-0.5868747603960375`, 
 0.13709660728856335`, 
 0.018223077560156144`}, {-0.5619323300904714`, 
 0.1370966072885633`, 0.010131794240974216`}}};

Теперь мы готовим грани и вершины

pt = Flatten[{datN[[1]], datN[[2]]}, 1];
facets = Join[{{Flatten@Map[Position[pt, #] &, datN[[1]]]}}, 
Table[{Flatten@
  Map[Position[pt, #] &, {datN[[1]][[i]], datN[[2]][[i]], 
    datN[[2]][[i + 1]], datN[[1]][[i + 1]]}]}, {i, 1, 
 10}], {{Flatten@Map[Position[pt, #] &, datN[[2]]]}}];

Затем мы используем TetGen в той же строке, как описано в документации для простейшего примера с блоком.

Needs["TetGenLink`"]
inInst = TetGenCreate[];
TetGenSetPoints[inInst, pt];
TetGenSetFacets[inInst, facets];
outInst = TetGenTetrahedralize[inInst, "pq1.414a0.01"];
coords = TetGenGetPoints[outInst];
surface = TetGenGetFaces[outInst];

Мы можем видеть, что сетка не генерируется, а также TetGenGetPoints не удалось перенастроить вершины. Результат очень неутешительный.

GraphicsGrid@{{Graphics3D[GraphicsComplex[pt, Map[Polygon, facets]], 
Boxed -> False], 
Graphics3D[GraphicsComplex[coords, Polygon[surface]]]}}

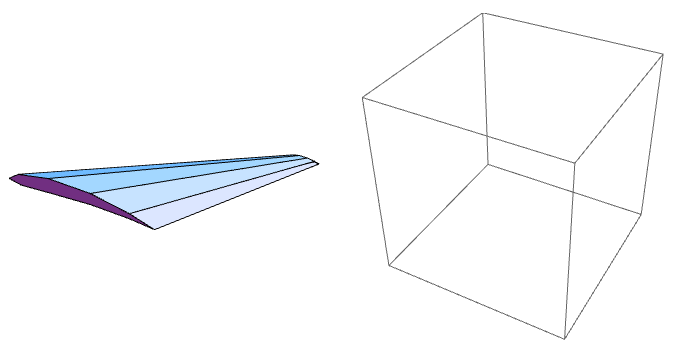
Почему происходит эта странная вещь? Документация TetGen также не является удовлетворительной.

Answer 1

Пока в datN Начальная и конечная точки двух подсписков фактически одинаковы, они считаются разными точками в отношении Mathematica. Это означает, что facets на самом деле не представляет собой замкнутый многогранник (между краями есть небольшой промежуток {datN[[1,1]], datN[[2,1]]} а также {datN[[1,-1]], datN[[2,-1]]}).

Чтобы решить эту проблему, вы можете отбросить конечные точки из datN[[1]] а также dat[[2]] и заменить любое вхождение datN[[i]][[11]] с datN[[i]][[1]] в определении facetsнапример,

datN2 = Drop[#, -1]& /@ datN;
pt = Flatten[datN2, 1];
facets = Join[
    {{Flatten@Map[Position[pt, #] &, datN2[[1]]]}}, 
    Table[{Flatten@
       Map[Position[pt, #] &, {datN2[[1]][[i]], datN2[[2]][[i]], 
         datN2[[2]][[Mod[i, 10] + 1]], 
         datN2[[1]][[Mod[i, 10] + 1]]}]}, {i, 1, 10}], 
    {{Flatten@Map[Position[pt, #] &, datN2[[2]]]}}];

Остальная часть кода остается прежней, т.е.

Needs["TetGenLink`"]
inInst = TetGenCreate[];
TetGenSetPoints[inInst, pt];
TetGenSetFacets[inInst, facets];
outInst = TetGenTetrahedralize[inInst, "pq1.414a0.01"];
coords = TetGenGetPoints[outInst];
surface = TetGenGetFaces[outInst];

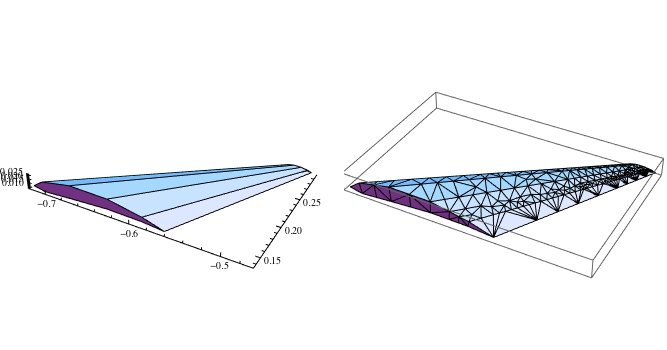
Затем построение поверхности дает следующий результат:

GraphicsGrid@{{Graphics3D[GraphicsComplex[pt, Map[Polygon, facets]], 
  Boxed -> False], 
Graphics3D[GraphicsComplex[coords, Polygon[surface]]]}}