Нарисуйте произвольную выпуклую форму, зная длину ее сторон

Question

У меня есть список значений, которые являются длинами сторон произвольной выпуклой формы (многоугольник). Как я могу нарисовать эту форму? Какой алгоритм может помочь мне с этой задачей?

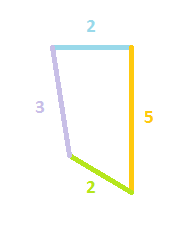
Например, у меня есть список: 2, 5, 2, 3. Рисунок должен выглядеть так:

Answer 1

Есть относительно простой (если немного тяжелый по математике) O(N log N) to O(N^2) (depending on implementation) решение рекурсивной геометрии / тригонометрии.

1. Концепция начинается с отрезка, длина которого равна сумме длин.
2. Разбейте этот отрезок на треугольник (см. Соответствующую информацию внизу).
3. Рекурсивно разбивайте каждый край треугольника на большее количество треугольников по мере необходимости.

Шаг 2, требует, чтобы два меньших края треугольника были длиннее, чем больший.

Шаг 3, можно сделать, превратив треугольник в 2 треугольника.

Для ввода и вывода я бы использовал: Input: список ребер Output: список внутренних углов.

Так output[a] внутренний угол вершины либо до, после края в input[a],

Хорошая ссылка находится здесь.

• Метод #1 gif, показывает треугольники для этого множества вершин.
• Метод № 2 gif, P является примером того, где разрыв может произойти на шаге 2.
• Метод #4 gif, здесь P можно считать перенесенным, как в #3, обратите внимание, что в этом случае длины линий не будут масштабироваться и фактически будут неизвестны. Обратите внимание, что только позиции вершин a1 а также a2 изменилось бы. В результате изменения внутренних углов вершин до и после a1 а также a2, В этом случае, a1,a2,a3,an,p,

Что касается определения внутренних углов. Используйте тригонометрию и / или геометрию. Учитывая 3 стороны треугольника, можно определить, каковы углы. Учитывая 2 стороны и угол (или 1 угол и 2 стороны) можно определить недостающие стороны и углы.

Конечно, вам, возможно, придется быть осторожным относительно того, где вы сломаете край, чтобы можно было сформировать треугольник.

Answer 2

Я процитирую здесь ответ, который я разместил на MathOverflow:

Цепочка ребер может закрыться, если длина самого длинного ребра не превышает сумму длин всех остальных ребер.

В вашем примере самый длинный край равен 5, и он не длиннее 2+2+3=7. Если вы замените ребро длины 5 ребром длины 8, то четыре сегмента не смогут приблизиться к выпуклому многоугольнику. Когда у вас есть более 3 ребер, результирующий выпуклый многоугольник определяется не однозначно: его форма имеет гибкость.

См. Ссылки, приведенные выше для указателей на доказательства.