Интерпретация выходных данных функции R bs() (матрица B-сплайнов)

Question

Я часто использую B-сплайны для регрессии. До сих пор мне никогда не нужно было понимать результаты bs подробно: я бы просто выбрал интересующую меня модель и соответствовал ей lm, Однако теперь мне нужно воспроизвести модель b-сплайна во внешнем (не R) коде. Итак, в чем смысл матрицы, сгенерированной bs? Пример:

x <- c(0.0, 11.0, 17.9, 49.3, 77.4)
bs(x, df = 3, degree = 1) # generate degree 1 (linear) B-splines with 2 internal knots
#              1         2         3
# [1,] 0.0000000 0.0000000 0.0000000    
# [2,] 0.8270677 0.0000000 0.0000000    
# [3,] 0.8198433 0.1801567 0.0000000    
# [4,] 0.0000000 0.7286085 0.2713915    
# [5,] 0.0000000 0.0000000 1.0000000   
# attr(,"degree")
# [1] 1
# attr(,"knots")
# 33.33333% 66.66667% 
#  13.30000  38.83333 
# attr(,"Boundary.knots")
# [1]  0.0 77.4
# attr(,"intercept")
# [1] FALSE
# attr(,"class")
# [1] "bs"     "basis"  "matrix"

Итак degree 1, как я указал на входе. knots говорит мне, что два внутренних узла находятся при х = 13,3000 и х = 38,8333 соответственно. Я был немного удивлен, увидев, что узлы находятся в фиксированных квантилях, я надеялся, что R найдет лучшие квантили для моих данных, но, конечно, это сделает модель не линейной, а также будет невозможной без знания данных ответа. intercept = FALSE означает, что в основу не был включен перехват (разве это хорошо? Меня всегда учили не подгонять линейные модели без перехвата... lm все равно просто добавляю один)

Однако как насчет матрицы? Я не очень понимаю, как это интерпретировать. Я думаю, что с тремя столбцами это означает, что базовых функций три. Это имеет смысл: если у меня есть два внутренних узла K1 а также K2У меня будет сплайн между левым краевым узлом B1 а также K1другой сплайн между K1 а также K2и последний между K2 а также B2, так что... три основные функции, хорошо. Но какие именно базовые функции? Например, что означает этот столбец?

#              1
# [1,] 0.0000000
# [2,] 0.8270677
# [3,] 0.8198433
# [4,] 0.0000000
# [5,] 0.0000000

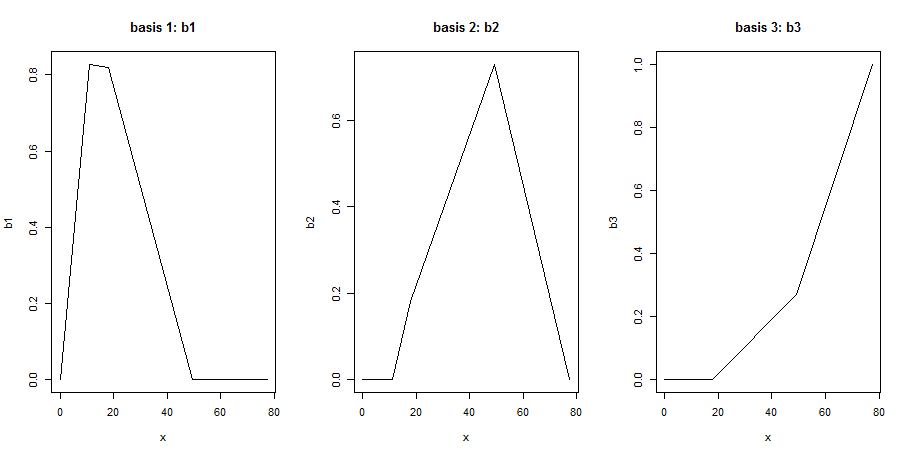
РЕДАКТИРОВАТЬ: это похоже, но не точно так же, как этот вопрос. Этот вопрос задает вопрос об интерпретации коэффициентов регрессии, но я на шаг впереди: я хотел бы понять значение коэффициентов матрицы модели. Если я пытаюсь составить те же сюжеты, которые были предложены в первом ответе, я получаю неправильный сюжет:

b <- bs(x, df = 3, degree = 1)
b1 <- b[, 1]  ## basis 1
b2 <- b[, 2]  ## basis 2
b3 <- b[,3]
par(mfrow = c(1, 3))
plot(x, b1, type = "l", main = "basis 1: b1")
plot(x, b2, type = "l", main = "basis 2: b2")
plot(x, b3, type = "l", main = "basis 3: b3")

Это не могут быть базисные функции B-сплайна, потому что у них слишком много узлов (у каждой функции должен быть только один).

Второй ответ на самом деле позволил бы мне восстановить мою модель вне R, так что, думаю, я мог бы пойти с этим. Тем не менее, также этот ответ не совсем объясняет, что элементы b Матрица: она имеет дело с коэффициентами линейной регрессии, которую я до сих пор не представил здесь. Это правда, что это моя конечная цель, но я хотел понять и этот промежуточный шаг.

Answer 1

Матрица b

#              1         2         3
# [1,] 0.0000000 0.0000000 0.0000000    
# [2,] 0.8270677 0.0000000 0.0000000    
# [3,] 0.8198433 0.1801567 0.0000000    
# [4,] 0.0000000 0.7286085 0.2713915    
# [5,] 0.0000000 0.0000000 1.0000000  

на самом деле просто матрица значений трех базисных функций в каждой точке x, что должно было быть для меня очевидно, так как это точно такая же интерпретация, как и для полиномиальной линейной модели. На самом деле, поскольку граничные узлы

bknots <- attr(b,"Boundary.knots")
# [1]  0.0 77.4

и внутренние узлы

iknots <- attr(b,"knots")
# 33.33333% 66.66667% 
#  13.30000  38.83333 

тогда три основные функции, как показано здесь:

knots <- c(bknots[1],iknots,bknots[2])
y1 <- c(0,1,0,0)
y2 <- c(0,0,1,0)
y3 <- c(0,0,0,1)
par(mfrow = c(1, 3))
plot(knots, y1, type = "l", main = "basis 1: b1")
plot(knots, y2, type = "l", main = "basis 2: b2")
plot(knots, b3, type = "l", main = "basis 3: b3")

Теперь рассмотрим b[,1]

#              1
# [1,] 0.0000000
# [2,] 0.8270677
# [3,] 0.8198433
# [4,] 0.0000000
# [5,] 0.0000000

Это должны быть значения b1 в x <- c(0.0, 11.0, 17.9, 49.3, 77.4), По сути дела, b1 0 в knots[1] = 0 и 1 в knots[2] = 13.3000Это означает, что в x[2] (11.0) значение должно быть 11/13.3 = 0.8270677, как и ожидалось. Точно так же, так как b1 0 для knots[3] = 38.83333, значение в x[3] (17.9) должно быть (38.83333-13.3)/17.9 = 0.8198433, поскольку x[4], x[5] > knots[3] = 38.83333, b1 там 0 Аналогичная интерпретация может быть дана для двух других столбцов.

Answer 2

Просто небольшая поправка к превосходному ответу @DeltaIV выше (похоже, я не могу комментировать.)

Так в b1когда он рассчитал b1(x[3]), так должно быть (38.83333-17.9)/(38.83333-13.3)=0.8198433 линейной интерполяцией. Все остальное идеально.

Запись b1 должен выглядеть так

\frac{t}{13.3}I(0<=t<13.3)+\frac{38.83333-t}{38.83333-13.3}I(13.3<=t<38.83333)