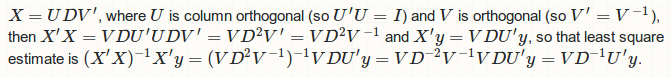Игрушечная функция R для решения обычных наименьших квадратов разложением по сингулярным числам

Question

Я пытаюсь написать функции для множественного регрессионного анализа (y = Xb + e) используя разложение по сингулярным числам для матриц. y а также X должен быть входным коэффициентом и вектором коэффициентов регрессии b, остаточный вектор e и дисперсия составляла R2 в качестве вывода. Ниже то, что у меня есть, и я полностью застрял. labels часть веса также дает мне ошибку. Что это labels часть? Кто-нибудь может дать мне несколько советов, которые помогут мне продолжить?

Test <- function(X, y) {
  x <- t(A) %*% A
  duv <- svd(x)
  x.inv <- duv$v %*% diag(1/duv$d) %*% t(duv$u)
  x.pseudo.inv <- x.inv %*% t(A)
  w <- x.pseudo.inv %*% labels
  return(b, e, R2)
  }

Answer 1

Вы с дороги... Декомпозиция сингулярного значения применяется к матрице модели X вместо нормальной матрицы X'X, Ниже приведена правильная процедура:

Таким образом, при написании функции R, мы должны сделать

svdOLS <- function (X, y) {
  SVD <- svd(X)
  V <- SVD$v
  U <- SVD$u
  D <- SVD$d
  ## regression coefficients `b`
  ## use `crossprod` for `U'y`
  ## use recycling rule for row rescaling of `U'y` by `D` inverse
  ## use `as.numeric` to return vector instead of matrix
  b <- as.numeric(V %*% (crossprod(U, y) / D))
  ## residuals
  r <- as.numeric(y - X %*% b)
  ## R-squared
  RSS <- crossprod(r)[1]
  TSS <- crossprod(y - mean(y))[1]
  R2 <- 1 - RSS / TSS
  ## multiple return via a list
  list(coefficients = b, residuals = r, R2 = R2)
  }

Давай проведем тест

## toy data
set.seed(0)
x1 <- rnorm(50); x2 <- rnorm(50); x3 <- rnorm(50); y <- rnorm(50)
X <- model.matrix(~ x1 + x2 + x3)

## fitting linear regression: y ~ x1 + x2 + x3
svdfit <- svdOLS(X, y)

#$coefficients
#[1]  0.14203754 -0.05699557 -0.01256007  0.09776255
#
#$residuals
# [1]  1.327108410 -1.400843739 -0.071885339  2.285661880  0.882041795
# [6] -0.535230752 -0.927750996  0.262674650 -0.133878558 -0.559783412
#[11]  0.264204296 -0.581468657  2.436913000  1.517601798  0.774515419
#[16]  0.447774149 -0.578988327  0.664690723 -0.511052627 -1.233302697
#[21]  1.740216739 -1.065592673 -0.332307898 -0.634125164 -0.975142054
#[26]  0.344995480 -1.748393187 -0.414763742 -0.680473508 -1.547232557
#[31] -0.383685601 -0.541602452 -0.827267878  0.894525453  0.359062906
#[36] -0.078656943  0.203938750 -0.813745178 -0.171993018  1.041370294
#[41] -0.114742717  0.034045040  1.888673004 -0.797999080  0.859074345
#[46]  1.664278354 -1.189408794  0.003618466 -0.527764821 -0.517902581
#
#$R2
#[1] 0.008276773

С другой стороны, мы можем использовать .lm.fit проверить правильность:

qrfit <- .lm.fit(X, y)

что точно так же по коэффициентам и остаткам:

all.equal(svdfit$coefficients, qrfit$coefficients)
# [1] TRUE

all.equal(svdfit$residuals, qrfit$residuals)
# [1] TRUE