GAM с "gp" более плавным: как получить параметры вариограммы?

Question

Я использую следующую геоаддитивную модель

library(gamair)
library(mgcv)

data(mack)    
mack$log.net.area <- log(mack$net.area)

gm2 <- gam(egg.count ~ s(lon,lat,bs="gp",k=100,m=c(2,10,1)) +
                       s(I(b.depth^.5)) +
                       s(c.dist) +
                       s(temp.20m) +
                       offset(log.net.area),
                       data = mack, family = tw, method = "REML")

Здесь я использую экспоненциальную ковариационную функцию с диапазоном = 10 и мощностью = 1 (m=c(2,10,1)). Как я могу получить из результатов параметры вариограммы (слепок, подоконник)? Я не смог ничего найти в выводе модели.

Answer 1

В подходе сглаживания указана корреляционная матрица, поэтому вы оцениваете только параметр дисперсии, т. Е. Порог. Например, вы установили m = c(2, 10, 1) в s(, bs = 'gp'), давая экспоненциальную матрицу корреляции с параметром диапазона phi = 10, Обратите внимание, что phi не совпадает с диапазоном, за исключением сферической корреляции. Для многих моделей корреляции фактический диапазон является функцией phi,

Параметр дисперсии / порога тесно связан с параметром сглаживания в штрафной регрессии, и вы можете получить его, разделив параметр масштаба на параметр сглаживания:

with(gm2, scale / sp["s(lon,lat)"])
#s(lon,lat) 
#  26.20877 

Это правильно? Нет. Здесь есть ловушка: параметры сглаживания возвращаются в $sp не настоящие, и нам нужно следующее:

gm2_sill <- with(gm2, scale / sp["s(lon,lat)"] * smooth[[1]]$S.scale) 
#s(lon,lat) 
#    7.7772 

И мы копируем в указанный вами параметр диапазона:

gm2_phi <- 10

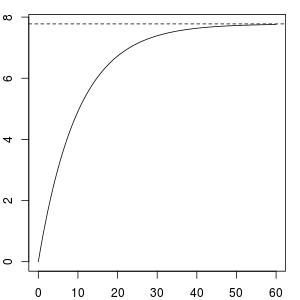
Самородок должен быть нулевым, поскольку гладкая функция непрерывна. С помощью lines.variomodel функция от geoR пакет, вы можете визуализировать вариограмму для скрытого гауссова пространственного случайного поля, моделируемого s(lon,lat),

library(geoR)
lines.variomodel(cov.model = "exponential", cov.pars = c(gm2_sill, gm2_phi),
                 nugget = 0, max.dist = 60)
abline(h = gm2_sill, lty = 2)

Однако будьте скептичны к этой вариограмме. mgcv не простая среда для интерпретации геостатистики. Использование сглаживателей низкого ранга предполагает, что вышеуказанный параметр дисперсии предназначен для параметров в новом пространстве параметров, а не в исходном. Например, есть 630 уникальных пространственных местоположений в пространственном поле для mack набор данных, поэтому матрица корреляции должна быть 630 x 630, а полные случайные эффекты должны быть вектором длины 630. Но, установив k = 100 в s(, bs = 'gp') усеченное собственное разложение и последующее приближение низкого ранга уменьшают случайные эффекты до длины-100. Параметр дисперсии действительно для этого вектора не является исходным. Это может объяснить, почему подоконник и фактический диапазон не согласуются с данными и предсказывают s(lon,lat),

## unique locations
loc <- unique(mack[, c("lon", "lat")])

max(dist(loc))
#[1] 15.98

Максимальное расстояние между двумя пространственными местоположениями в наборе данных составляет 15,98, но реальный диапазон от вариограммы кажется где-то между 40 и 60, что слишком велико.

## predict `s(lon, lat)`, using the method I told you in your last question
## https://stackru.com/q/51634953/4891738
sp <- predict(gm2,
              data.frame(loc, b.depth = 0, c.dist = 0, temp.20m = 0,
                         log.net.area = 0),
              type = "terms", terms = "s(lon,lat)")

c(var(sp))
#[1] 1.587126

Предсказанный s(lon,lat) имеет только дисперсию 1,587, но порог 7,77 намного выше.