Алгоритм 2D Raytracer

Question

Я хочу сделать программно RayTracer в Java для демонстрационных целей, когда я делаю презентацию о Ray Tracing в целом (также с упоминанием 3D, эта 2D-модель должна быть только для облегчения понимания и для обучения моим общим знаниям Java).

Моя проблема в том, что я не знаю, с чего начать все это.

Первое, что я хотел бы попробовать, это использовать векторы для отслеживания каждого пикселя на экране по заданной координате (например, положение моего курсора мыши). Тогда я бы вычислил, если вектор пересекается с многоугольником, а затем остановил бы вектор и нарисовал его только в этой конкретной точке.

Возможно, я мог бы даже нарисовать некоторые тени, вычислив нормаль и отразив вектор в другом направлении с меньшей интенсивностью.

Так что было бы неплохо нарисовать вектор из A = {everypixelonthescreen} к конкретному Point P и рассчитать пересечения?

Готовая версия должна выглядеть примерно так:

Answer 1

Я боюсь, что такого рода приложение трассировки лучей, которое вы предлагаете, немного вводит в заблуждение, чем использование реального 3D-трассировщика лучей.

• 2D трассеры лучей используются немного по-другому
• и это может сильно запутать вашу аудиторию

Я бы попробовал выбрать более родное использование 2D-трассировки лучей, например:

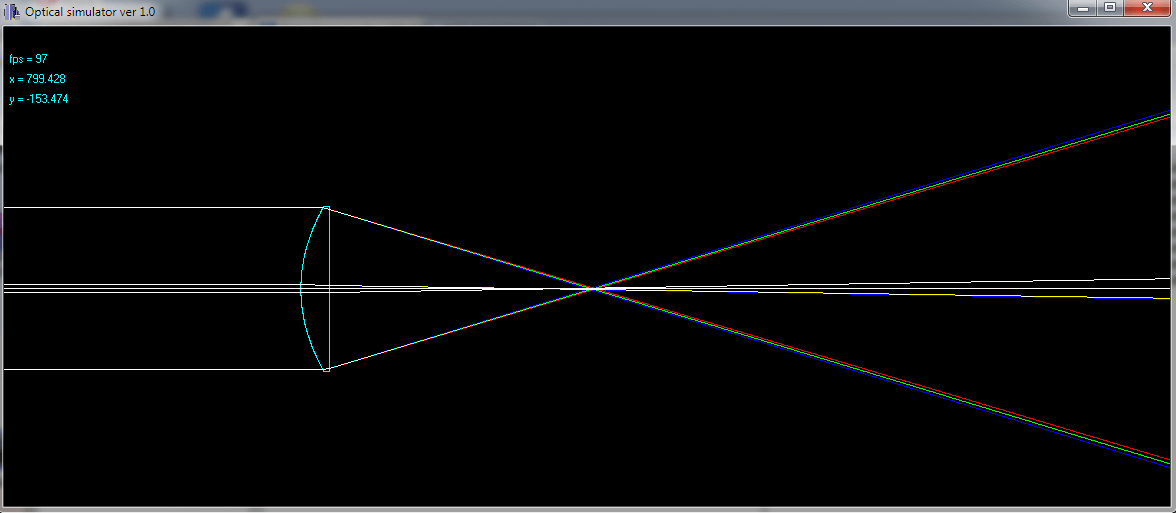
1. Оптическое моделирование

   Это используется для имитации оптики линз и зеркал. Вот изображение из одного из моих древних 2D-симуляций трассировки лучей:

   

   1. Храните свой мир

      Вы получили линзу в виде полилиний + дифракционный индекс и зеркала также как полилинии. У вас есть мировой индекс дифракции

   2. излучать лучи R,G,B от источника света

      В ролях только важные или все. Используйте закон Снелла для симуляции оптики

   Как вы можете видеть, хроматическая ошибка видна (каждый цвет имеет свою собственную длину волны, поэтому дифракционный индекс отличается). Вы также можете использовать MultiBand рендеринг.

   Я использовал это для настройки пользовательских оптических систем, если вы добавили возможность перетаскивания мышью и получили Optic Lab

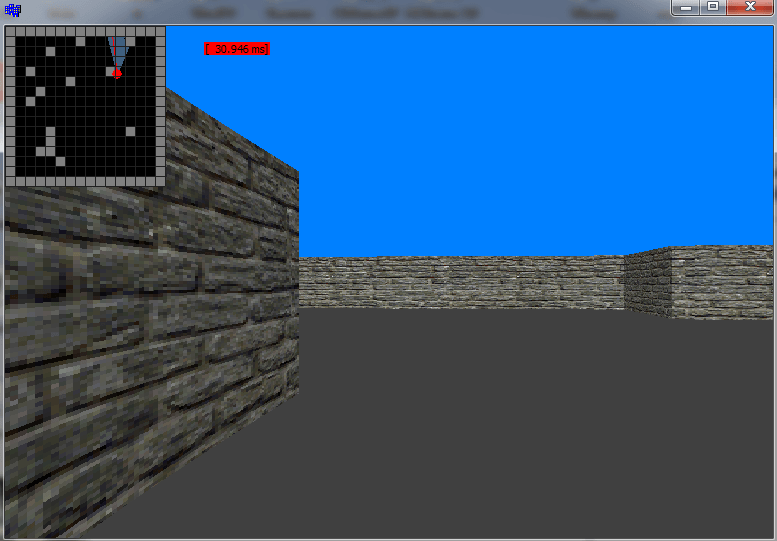
2. Wolfenstein demo

   Эта псевдо 3D игра использовала движок 2D лучей, см. https://en.wikipedia.org/wiki/Wolfenstein_3D_engine. Это изображение было взято из этой ссылки:

   

   1. Сначала нарисуйте пол и потолок / небо как две половины экрана (экран разделен по горизонтали)

   2. тогда вы получили 2D карту вашего лабиринта / мира (справа)

      Поэтому излучайте лучи от вашего текущего положения во всех видимых направлениях (аналогично вашему изображению, но обычно используется угол обзора 60 градусов). Лучи должны быть сделаны с точностью до субпикселя (ячейки). где ваш луч врезается в стену (на карте), получите позицию субпикселя (ячейки). Указывает, какая часть текстуры стены поражена

   3. Нарисуйте соответствующий столбец (вертикальную линию) на экране для каждого попадания луча

      Размер и масштаб его определяются расстоянием от источника луча. Коррекция "рыбий глаз" применяется, если моя память не изменяет, это было сделано с использованием только перпендикулярного расстояния (умножьте расстояние на cos(ray_angle-player_angle)).

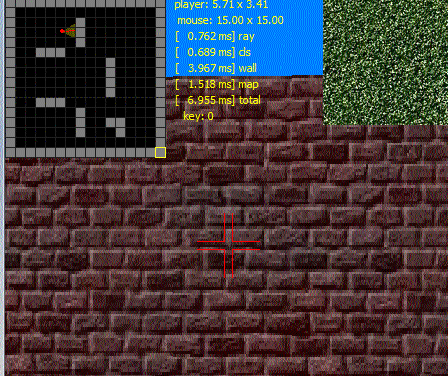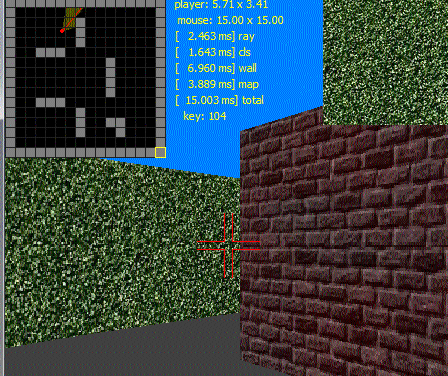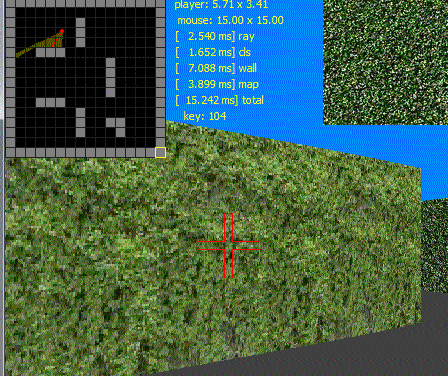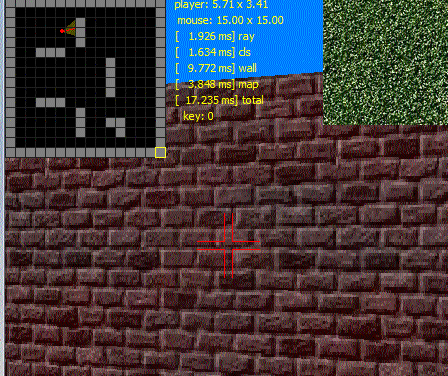
   Вот пример того, что я только что развел для удовольствия:

   

   Это делается в C++ с использованием чистого GDI (с использованием только строки растрового сканирования), без каких-либо других сторонних библиотек. Он использует одиночную текстуру, рассеянное + окружающее освещение, 2D лучевое вещание. Имеет 2 растровых изображения (экран, текстура-атлас) и одну 2D-карту. Код менее 9 Кбайт, включая rems. Он управляется только с клавиатуры (мышь используется для редактирования лабиринта в подокне карты).

   Вот анимированный пример GIF:

   

   Если вам интересно, посмотрите соответствующий QA:

   • Вольфенштейн с переменной высотой клеток

Answer 2

Насколько я понимаю, к этому вопросу можно подходить иначе. Учитывая некоторую позицию (текущую позицию мыши или что-то подобное), среда будет отслеживаться оттуда в диапазоне некоторого заданного угла (например, 90 градусов, на вашей фотографии это выглядит как 360 градусов). При желаемом разрешении угла лучи из исходного положения пересекаются с упомянутыми многоугольниками. Ближайшие точки пересечения оказываются. Этот подход должен визуализировать точки, которые "видны" с данной позиции.