Кривая Catmull-rom без острых выступов и самопересечений
У меня есть следующий код для расчета точек между четырьмя контрольными точками для создания кривой Catmull-rom:
CGPoint interpolatedPosition(CGPoint p0, CGPoint p1, CGPoint p2, CGPoint p3, float t)
{
float t3 = t * t * t;
float t2 = t * t;
float f1 = -0.5 * t3 + t2 - 0.5 * t;
float f2 = 1.5 * t3 - 2.5 * t2 + 1.0;
float f3 = -1.5 * t3 + 2.0 * t2 + 0.5 * t;
float f4 = 0.5 * t3 - 0.5 * t2;
float x = p0.x * f1 + p1.x * f2 + p2.x * f3 + p3.x * f4;
float y = p0.y * f1 + p1.y * f2 + p2.y * f3 + p3.y * f4;
return CGPointMake(x, y);
}
Это прекрасно работает, но я хочу создать то, что, я думаю, называется центростремительной параметризацией. Это означает, что кривая не будет иметь выступов и самопересечений. Если я переместлю одну контрольную точку очень близко к другой, кривая должна стать "меньше". Я погуглил глаза, пытаясь найти способ сделать это. Кто-нибудь знает, как это сделать?
5 ответов
Мне нужно было реализовать это и для работы. Фундаментальная концепция, с которой нужно начать, заключается в том, что основное отличие между обычной реализацией Catmull-Rom и модифицированными версиями заключается в том, как они обрабатывают время.
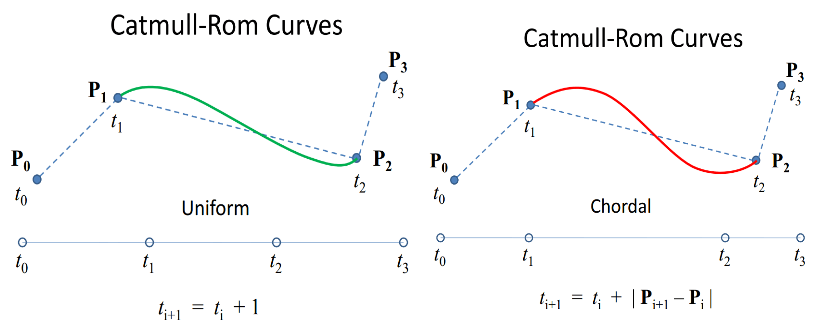
В непараметрической версии из вашей первоначальной реализации Catmull-Rom t начинается с 0 и заканчивается 1 и вычисляет кривую от P1 до P2. В параметризованной реализации времени t начинается с 0 в P0 и продолжает увеличиваться во всех четырех точках. Так что в едином случае это будет 1 в P1 и 2 в P2, и вы будете передавать значения в диапазоне от 1 до 2 для вашей интерполяции.
Аккордовый случай показывает |Pi+1 - P| как изменение времени Это просто означает, что вы можете использовать расстояние по прямой линии между точками каждого сегмента, чтобы вычислить фактическую длину для использования. В центростремительном случае просто используется немного другой метод для расчета оптимальной продолжительности времени для каждого сегмента.
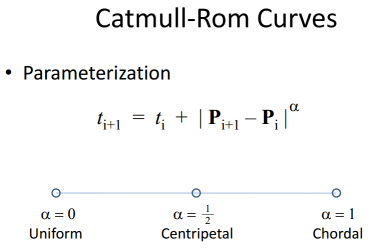
Так что теперь нам просто нужно знать, как придумать уравнения, которые позволят нам включить наши новые значения времени. Типичное уравнение Кэтмалла-Рома содержит только одну t, время, для которого вы пытаетесь вычислить значение. Я нашел лучшую статью для описания того, как эти параметры рассчитываются здесь: http://www.cemyuksel.com/research/catmullrom_param/catmullrom.pdf. Они были сосредоточены на математической оценке кривых, но в этом заключается ключевая формула Барри и Голдмана.(1)
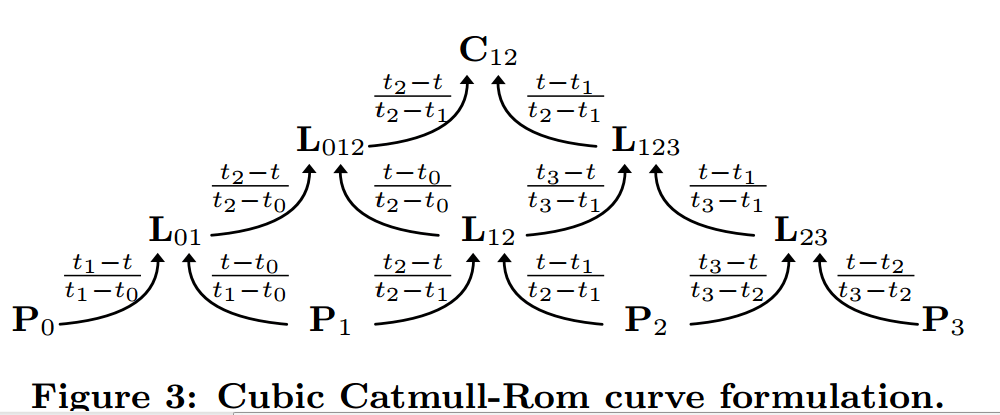
На приведенной выше диаграмме стрелки означают "умноженное на" соотношение, указанное в стрелке.
Затем это дает нам то, что нам нужно для выполнения вычисления, чтобы получить желаемый результат. X и Y рассчитываются независимо, хотя я использовал коэффициент "Расстояние" для изменения времени на основе 2D-расстояния, а не 1D-расстояния.
Результаты теста:
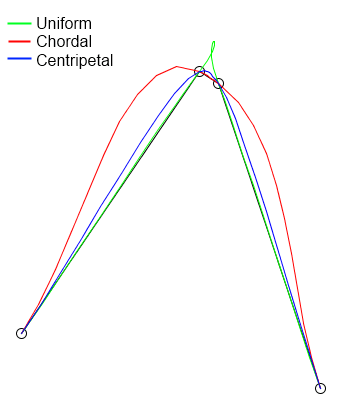
(1) Пи Джей Барри и Р. Н. Голдман. Алгоритм рекурсивной оценки для класса сплайнов Кэт-Малла. SIGGRAPH Computer Graphics, 22(4):199{204, 1988.
Исходный код для моей окончательной реализации на Java выглядит следующим образом:
/**
* This method will calculate the Catmull-Rom interpolation curve, returning
* it as a list of Coord coordinate objects. This method in particular
* adds the first and last control points which are not visible, but required
* for calculating the spline.
*
* @param coordinates The list of original straight line points to calculate
* an interpolation from.
* @param pointsPerSegment The integer number of equally spaced points to
* return along each curve. The actual distance between each
* point will depend on the spacing between the control points.
* @return The list of interpolated coordinates.
* @param curveType Chordal (stiff), Uniform(floppy), or Centripetal(medium)
* @throws gov.ca.water.shapelite.analysis.CatmullRomException if
* pointsPerSegment is less than 2.
*/
public static List<Coord> interpolate(List<Coord> coordinates, int pointsPerSegment, CatmullRomType curveType)
throws CatmullRomException {
List<Coord> vertices = new ArrayList<>();
for (Coord c : coordinates) {
vertices.add(c.copy());
}
if (pointsPerSegment < 2) {
throw new CatmullRomException("The pointsPerSegment parameter must be greater than 2, since 2 points is just the linear segment.");
}
// Cannot interpolate curves given only two points. Two points
// is best represented as a simple line segment.
if (vertices.size() < 3) {
return vertices;
}
// Test whether the shape is open or closed by checking to see if
// the first point intersects with the last point. M and Z are ignored.
boolean isClosed = vertices.get(0).intersects2D(vertices.get(vertices.size() - 1));
if (isClosed) {
// Use the second and second from last points as control points.
// get the second point.
Coord p2 = vertices.get(1).copy();
// get the point before the last point
Coord pn1 = vertices.get(vertices.size() - 2).copy();
// insert the second from the last point as the first point in the list
// because when the shape is closed it keeps wrapping around to
// the second point.
vertices.add(0, pn1);
// add the second point to the end.
vertices.add(p2);
} else {
// The shape is open, so use control points that simply extend
// the first and last segments
// Get the change in x and y between the first and second coordinates.
double dx = vertices.get(1).X - vertices.get(0).X;
double dy = vertices.get(1).Y - vertices.get(0).Y;
// Then using the change, extrapolate backwards to find a control point.
double x1 = vertices.get(0).X - dx;
double y1 = vertices.get(0).Y - dy;
// Actaully create the start point from the extrapolated values.
Coord start = new Coord(x1, y1, vertices.get(0).Z);
// Repeat for the end control point.
int n = vertices.size() - 1;
dx = vertices.get(n).X - vertices.get(n - 1).X;
dy = vertices.get(n).Y - vertices.get(n - 1).Y;
double xn = vertices.get(n).X + dx;
double yn = vertices.get(n).Y + dy;
Coord end = new Coord(xn, yn, vertices.get(n).Z);
// insert the start control point at the start of the vertices list.
vertices.add(0, start);
// append the end control ponit to the end of the vertices list.
vertices.add(end);
}
// Dimension a result list of coordinates.
List<Coord> result = new ArrayList<>();
// When looping, remember that each cycle requires 4 points, starting
// with i and ending with i+3. So we don't loop through all the points.
for (int i = 0; i < vertices.size() - 3; i++) {
// Actually calculate the Catmull-Rom curve for one segment.
List<Coord> points = interpolate(vertices, i, pointsPerSegment, curveType);
// Since the middle points are added twice, once for each bordering
// segment, we only add the 0 index result point for the first
// segment. Otherwise we will have duplicate points.
if (result.size() > 0) {
points.remove(0);
}
// Add the coordinates for the segment to the result list.
result.addAll(points);
}
return result;
}
/**
* Given a list of control points, this will create a list of pointsPerSegment
* points spaced uniformly along the resulting Catmull-Rom curve.
*
* @param points The list of control points, leading and ending with a
* coordinate that is only used for controling the spline and is not visualized.
* @param index The index of control point p0, where p0, p1, p2, and p3 are
* used in order to create a curve between p1 and p2.
* @param pointsPerSegment The total number of uniformly spaced interpolated
* points to calculate for each segment. The larger this number, the
* smoother the resulting curve.
* @param curveType Clarifies whether the curve should use uniform, chordal
* or centripetal curve types. Uniform can produce loops, chordal can
* produce large distortions from the original lines, and centripetal is an
* optimal balance without spaces.
* @return the list of coordinates that define the CatmullRom curve
* between the points defined by index+1 and index+2.
*/
public static List<Coord> interpolate(List<Coord> points, int index, int pointsPerSegment, CatmullRomType curveType) {
List<Coord> result = new ArrayList<>();
double[] x = new double[4];
double[] y = new double[4];
double[] time = new double[4];
for (int i = 0; i < 4; i++) {
x[i] = points.get(index + i).X;
y[i] = points.get(index + i).Y;
time[i] = i;
}
double tstart = 1;
double tend = 2;
if (!curveType.equals(CatmullRomType.Uniform)) {
double total = 0;
for (int i = 1; i < 4; i++) {
double dx = x[i] - x[i - 1];
double dy = y[i] - y[i - 1];
if (curveType.equals(CatmullRomType.Centripetal)) {
total += Math.pow(dx * dx + dy * dy, .25);
} else {
total += Math.pow(dx * dx + dy * dy, .5);
}
time[i] = total;
}
tstart = time[1];
tend = time[2];
}
double z1 = 0.0;
double z2 = 0.0;
if (!Double.isNaN(points.get(index + 1).Z)) {
z1 = points.get(index + 1).Z;
}
if (!Double.isNaN(points.get(index + 2).Z)) {
z2 = points.get(index + 2).Z;
}
double dz = z2 - z1;
int segments = pointsPerSegment - 1;
result.add(points.get(index + 1));
for (int i = 1; i < segments; i++) {
double xi = interpolate(x, time, tstart + (i * (tend - tstart)) / segments);
double yi = interpolate(y, time, tstart + (i * (tend - tstart)) / segments);
double zi = z1 + (dz * i) / segments;
result.add(new Coord(xi, yi, zi));
}
result.add(points.get(index + 2));
return result;
}
/**
* Unlike the other implementation here, which uses the default "uniform"
* treatment of t, this computation is used to calculate the same values but
* introduces the ability to "parameterize" the t values used in the
* calculation. This is based on Figure 3 from
* http://www.cemyuksel.com/research/catmullrom_param/catmullrom.pdf
*
* @param p An array of double values of length 4, where interpolation
* occurs from p1 to p2.
* @param time An array of time measures of length 4, corresponding to each
* p value.
* @param t the actual interpolation ratio from 0 to 1 representing the
* position between p1 and p2 to interpolate the value.
* @return
*/
public static double interpolate(double[] p, double[] time, double t) {
double L01 = p[0] * (time[1] - t) / (time[1] - time[0]) + p[1] * (t - time[0]) / (time[1] - time[0]);
double L12 = p[1] * (time[2] - t) / (time[2] - time[1]) + p[2] * (t - time[1]) / (time[2] - time[1]);
double L23 = p[2] * (time[3] - t) / (time[3] - time[2]) + p[3] * (t - time[2]) / (time[3] - time[2]);
double L012 = L01 * (time[2] - t) / (time[2] - time[0]) + L12 * (t - time[0]) / (time[2] - time[0]);
double L123 = L12 * (time[3] - t) / (time[3] - time[1]) + L23 * (t - time[1]) / (time[3] - time[1]);
double C12 = L012 * (time[2] - t) / (time[2] - time[1]) + L123 * (t - time[1]) / (time[2] - time[1]);
return C12;
}
Существует гораздо более простой и эффективный способ реализации этого, который требует лишь вычисления ваших касательных с использованием другой формулы без необходимости реализации алгоритма рекурсивной оценки Барри и Голдмана.
Если вы возьмете параметризацию Барри-Голдмана (на которую ссылается ответ Теда) C(t) для узлов (t0,t1,t2,t3) и контрольных точек (P0,P1,P2,P3), ее замкнутая форма будет довольно сложной, но в конце это все еще кубический многочлен от t, когда вы ограничиваете его интервалом (t1,t2). Таким образом, все, что нам нужно, чтобы полностью описать это, это значения и касательные в двух конечных точках t1 и t2. Если мы разработаем эти значения (я сделал это в Mathematica), мы найдем
C(t1) = P1
C(t2) = P2
C'(t1) = (P1 - P0) / (t1 - t0) - (P2 - P0) / (t2 - t0) + (P2 - P1) / (t2 - t1)
C'(t2) = (P2 - P1) / (t2 - t1) - (P3 - P1) / (t3 - t1) + (P3 - P2) / (t3 - t2)
Мы можем просто вставить это в стандартную формулу для вычисления кубического сплайна с заданными значениями и касательными в конечных точках, и у нас есть наш неоднородный сплайн Катмулла-Рома. Одно предостережение заключается в том, что вышеуказанные касательные вычисляются для интервала (t1,t2), поэтому, если вы хотите оценить кривую в стандартном интервале (0,1), просто измените масштаб касательных, умножив их на коэффициент (t2-t1).).
Я поставил рабочий пример C++ на Ideone: http://ideone.com/NoEbVM
Я также вставлю код ниже.
#include <iostream>
#include <cmath>
using namespace std;
struct CubicPoly
{
float c0, c1, c2, c3;
float eval(float t)
{
float t2 = t*t;
float t3 = t2 * t;
return c0 + c1*t + c2*t2 + c3*t3;
}
};
/*
* Compute coefficients for a cubic polynomial
* p(s) = c0 + c1*s + c2*s^2 + c3*s^3
* such that
* p(0) = x0, p(1) = x1
* and
* p'(0) = t0, p'(1) = t1.
*/
void InitCubicPoly(float x0, float x1, float t0, float t1, CubicPoly &p)
{
p.c0 = x0;
p.c1 = t0;
p.c2 = -3*x0 + 3*x1 - 2*t0 - t1;
p.c3 = 2*x0 - 2*x1 + t0 + t1;
}
// standard Catmull-Rom spline: interpolate between x1 and x2 with previous/following points x0/x3
// (we don't need this here, but it's for illustration)
void InitCatmullRom(float x0, float x1, float x2, float x3, CubicPoly &p)
{
// Catmull-Rom with tension 0.5
InitCubicPoly(x1, x2, 0.5f*(x2-x0), 0.5f*(x3-x1), p);
}
// compute coefficients for a nonuniform Catmull-Rom spline
void InitNonuniformCatmullRom(float x0, float x1, float x2, float x3, float dt0, float dt1, float dt2, CubicPoly &p)
{
// compute tangents when parameterized in [t1,t2]
float t1 = (x1 - x0) / dt0 - (x2 - x0) / (dt0 + dt1) + (x2 - x1) / dt1;
float t2 = (x2 - x1) / dt1 - (x3 - x1) / (dt1 + dt2) + (x3 - x2) / dt2;
// rescale tangents for parametrization in [0,1]
t1 *= dt1;
t2 *= dt1;
InitCubicPoly(x1, x2, t1, t2, p);
}
struct Vec2D
{
Vec2D(float _x, float _y) : x(_x), y(_y) {}
float x, y;
};
float VecDistSquared(const Vec2D& p, const Vec2D& q)
{
float dx = q.x - p.x;
float dy = q.y - p.y;
return dx*dx + dy*dy;
}
void InitCentripetalCR(const Vec2D& p0, const Vec2D& p1, const Vec2D& p2, const Vec2D& p3,
CubicPoly &px, CubicPoly &py)
{
float dt0 = powf(VecDistSquared(p0, p1), 0.25f);
float dt1 = powf(VecDistSquared(p1, p2), 0.25f);
float dt2 = powf(VecDistSquared(p2, p3), 0.25f);
// safety check for repeated points
if (dt1 < 1e-4f) dt1 = 1.0f;
if (dt0 < 1e-4f) dt0 = dt1;
if (dt2 < 1e-4f) dt2 = dt1;
InitNonuniformCatmullRom(p0.x, p1.x, p2.x, p3.x, dt0, dt1, dt2, px);
InitNonuniformCatmullRom(p0.y, p1.y, p2.y, p3.y, dt0, dt1, dt2, py);
}
int main()
{
Vec2D p0(0,0), p1(1,1), p2(1.1,1), p3(2,0);
CubicPoly px, py;
InitCentripetalCR(p0, p1, p2, p3, px, py);
for (int i = 0; i <= 10; ++i)
cout << px.eval(0.1f*i) << " " << py.eval(0.1f*i) << endl;
}
Вот iOS-версия кода Теда. Я исключил части 'z'.
.час
typedef enum {
CatmullRomTypeUniform,
CatmullRomTypeChordal,
CatmullRomTypeCentripetal
} CatmullRomType ;
.m
-(NSMutableArray *)interpolate:(NSArray *)coordinates withPointsPerSegment:(NSInteger)pointsPerSegment andType:(CatmullRomType)curveType {
NSMutableArray *vertices = [[NSMutableArray alloc] initWithArray:coordinates copyItems:YES];
if (pointsPerSegment < 3)
return vertices;
//start point
CGPoint pt1 = [vertices[0] CGPointValue];
CGPoint pt2 = [vertices[1] CGPointValue];
double dx = pt2.x - pt1.x;
double dy = pt2.y - pt1.y;
double x1 = pt1.x - dx;
double y1 = pt1.y - dy;
CGPoint start = CGPointMake(x1*.5, y1);
//end point
pt2 = [vertices[vertices.count-1] CGPointValue];
pt1 = [vertices[vertices.count-2] CGPointValue];
dx = pt2.x - pt1.x;
dy = pt2.y - pt1.y;
x1 = pt2.x + dx;
y1 = pt2.y + dy;
CGPoint end = CGPointMake(x1, y1);
[vertices insertObject:[NSValue valueWithCGPoint:start] atIndex:0];
[vertices addObject:[NSValue valueWithCGPoint:end]];
NSMutableArray *result = [[NSMutableArray alloc] init];
for (int i = 0; i < vertices.count - 3; i++) {
NSMutableArray *points = [self interpolate:vertices forIndex:i withPointsPerSegment:pointsPerSegment andType:curveType];
if ([points count] > 0)
[points removeObjectAtIndex:0];
[result addObjectsFromArray:points];
}
return result;
}
-(double)interpolate:(double*)p time:(double*)time t:(double) t {
double L01 = p[0] * (time[1] - t) / (time[1] - time[0]) + p[1] * (t - time[0]) / (time[1] - time[0]);
double L12 = p[1] * (time[2] - t) / (time[2] - time[1]) + p[2] * (t - time[1]) / (time[2] - time[1]);
double L23 = p[2] * (time[3] - t) / (time[3] - time[2]) + p[3] * (t - time[2]) / (time[3] - time[2]);
double L012 = L01 * (time[2] - t) / (time[2] - time[0]) + L12 * (t - time[0]) / (time[2] - time[0]);
double L123 = L12 * (time[3] - t) / (time[3] - time[1]) + L23 * (t - time[1]) / (time[3] - time[1]);
double C12 = L012 * (time[2] - t) / (time[2] - time[1]) + L123 * (t - time[1]) / (time[2] - time[1]);
return C12;
}
-(NSMutableArray*)interpolate:(NSArray *)points forIndex:(NSInteger)index withPointsPerSegment:(NSInteger)pointsPerSegment andType:(CatmullRomType)curveType {
NSMutableArray *result = [[NSMutableArray alloc] init];
double x[4];
double y[4];
double time[4];
for (int i=0; i < 4; i++) {
x[i] = [points[index+i] CGPointValue].x;
y[i] = [points[index+i] CGPointValue].y;
time[i] = i;
}
double tstart = 1;
double tend = 2;
if (curveType != CatmullRomTypeUniform) {
double total = 0;
for (int i=1; i < 4; i++) {
double dx = x[i] - x[i-1];
double dy = y[i] - y[i-1];
if (curveType == CatmullRomTypeCentripetal) {
total += pow(dx * dx + dy * dy, 0.25);
}
else {
total += pow(dx * dx + dy * dy, 0.5); //sqrt
}
time[i] = total;
}
tstart = time[1];
tend = time[2];
}
int segments = pointsPerSegment - 1;
[result addObject:points[index+1]];
for (int i =1; i < segments; i++) {
double xi = [self interpolate:x time:time t:tstart + (i * (tend - tstart)) / segments];
double yi = [self interpolate:y time:time t:tstart + (i * (tend - tstart)) / segments];
NSLog(@"(%f,%f)",xi,yi);
[result addObject:[NSValue valueWithCGPoint:CGPointMake(xi, yi)]];
}
[result addObject:points[index+2]];
return result;
}
Кроме того, вот метод для превращения массива точек в путь Безье для рисования, используя выше
-(UIBezierPath*)bezierPathFromPoints:(NSArray *)points withGranulaity:(NSInteger)granularity
{
UIBezierPath __block *path = [[UIBezierPath alloc] init];
NSMutableArray *curve = [self interpolate:points withPointsPerSegment:granularity andType:CatmullRomTypeCentripetal];
CGPoint __block p0 = [curve[0] CGPointValue];
[path moveToPoint:p0];
//use this loop to draw lines between all points
for (int idx=1; idx < [curve count]; idx+=1) {
CGPoint c1 = [curve[idx] CGPointValue];
[path addLineToPoint:c1];
};
//or use this loop to use actual control points (less smooth but probably faster)
// for (int idx=0; idx < [curve count]-3; idx+=3) {
// CGPoint c1 = [curve[idx+1] CGPointValue];
// CGPoint c2 = [curve[idx+2] CGPointValue];
// CGPoint p1 = [curve[idx+3] CGPointValue];
//
// [path addCurveToPoint:p1 controlPoint1:c1 controlPoint2:c2];
// };
return path;
}
Спасибо за ответ Теда и cfh.
Извините за мой плохой английский, и я не очень уверен, что я правильно понимаю.
Раньше меня смущало то, какова связь между и «Параметризацией кривых Катмулла-Рома» [Юксель и другие. 2009].
В конце концов кажется, что это имеет мало отношения к.
В ответе Теда мы можем обнаружить, что до тех пор, пока мы называем это «равномерной» кривой Катмулла-Рома. Итак, все кривые в являются «однородными» кривыми, в то время как параметризованный Catmull-Rom может дать только одну «однородную» кривая когда. просто влияет на то, насколько резко кривая изгибается в (интерполированных) контрольных точках, и может создавать серию «однородных» кривых.
Здесь, если мы примем во внимание уравнение из cfh, то есть:
C(t1) = P1
C(t2) = P2
C'(t1) = (P1 - P0) / (t1 - t0) - (P2 - P0) / (t2 - t0) + (P2 - P1) / (t2 - t1)
C'(t2) = (P2 - P1) / (t2 - t1) - (P3 - P1) / (t3 - t1) + (P3 - P2) / (t3 - t2)
Когда
α=0, мы знаем это . Подстановка
t(i+1)-t(i)=1 к
C'(t1) и
C'(t2), мы можем получить:
C'(t1)=1/2(P2-P0)
C'(t2)=1/2(P3-P1).
Другими словами, единственная «однородная» кривая, порожденная параметризованной кривой Катмулла-Рома, соответствует частному случаю
τ=1/2 http://graphics.cs.cmu.edu/nsp/course/15-462/Fall04/assts/catmullRom.pdf . Более разные «однородные» кривые могут быть получены путем изменения
τ, пока
α уделяет больше внимания другому.
Я написал что-то на Python (адаптированная форма страницы Википедии Catmull-Rom), в котором сравниваются унифицированные, центростремительные и хордовые сплайны CR (хотя вы можете установить альфа на любое значение) с использованием случайных данных (вы можете использовать свои собственные данные и функции). работает нормально). Обратите внимание, что для конечных точек я просто застрял в быстром "хаке", который поддерживает наклон от первой и последней 2 точек, хотя расстояние между этой точкой и первой / потерянной известной точкой является произвольным (я установил его на 1% от домен... без всякой причины. Так что имейте это в виду, прежде чем обратиться к чему-то важному):
# coding: utf-8
# In[1]:
import numpy
import matplotlib.pyplot as plt
get_ipython().magic(u'pylab inline')
# In[2]:
def CatmullRomSpline(P0, P1, P2, P3, a, nPoints=100):
"""
P0, P1, P2, and P3 should be (x,y) point pairs that define the Catmull-Rom spline.
nPoints is the number of points to include in this curve segment.
"""
# Convert the points to numpy so that we can do array multiplication
P0, P1, P2, P3 = map(numpy.array, [P0, P1, P2, P3])
# Calculate t0 to t4
alpha = a
def tj(ti, Pi, Pj):
xi, yi = Pi
xj, yj = Pj
return ( ( (xj-xi)**2 + (yj-yi)**2 )**0.5 )**alpha + ti
t0 = 0
t1 = tj(t0, P0, P1)
t2 = tj(t1, P1, P2)
t3 = tj(t2, P2, P3)
# Only calculate points between P1 and P2
t = numpy.linspace(t1,t2,nPoints)
# Reshape so that we can multiply by the points P0 to P3
# and get a point for each value of t.
t = t.reshape(len(t),1)
A1 = (t1-t)/(t1-t0)*P0 + (t-t0)/(t1-t0)*P1
A2 = (t2-t)/(t2-t1)*P1 + (t-t1)/(t2-t1)*P2
A3 = (t3-t)/(t3-t2)*P2 + (t-t2)/(t3-t2)*P3
B1 = (t2-t)/(t2-t0)*A1 + (t-t0)/(t2-t0)*A2
B2 = (t3-t)/(t3-t1)*A2 + (t-t1)/(t3-t1)*A3
C = (t2-t)/(t2-t1)*B1 + (t-t1)/(t2-t1)*B2
return C
def CatmullRomChain(P,alpha):
"""
Calculate Catmull Rom for a chain of points and return the combined curve.
"""
sz = len(P)
# The curve C will contain an array of (x,y) points.
C = []
for i in range(sz-3):
c = CatmullRomSpline(P[i], P[i+1], P[i+2], P[i+3],alpha)
C.extend(c)
return C
# In[8]:
# Define a set of points for curve to go through
Points = numpy.random.rand(12,2)
x1=Points[0][0]
x2=Points[1][0]
y1=Points[0][1]
y2=Points[1][1]
x3=Points[-2][0]
x4=Points[-1][0]
y3=Points[-2][1]
y4=Points[-1][1]
dom=max(Points[:,0])-min(Points[:,0])
rng=max(Points[:,1])-min(Points[:,1])
prex=x1+sign(x1-x2)*dom*0.01
prey=(y1-y2)/(x1-x2)*dom*0.01+y1
endx=x4+sign(x4-x3)*dom*0.01
endy=(y4-y3)/(x4-x3)*dom*0.01+y4
print len(Points)
Points=list(Points)
Points.insert(0,array([prex,prey]))
Points.append(array([endx,endy]))
print len(Points)
# In[9]:
#Define alpha
a=0.
# Calculate the Catmull-Rom splines through the points
c = CatmullRomChain(Points,a)
# Convert the Catmull-Rom curve points into x and y arrays and plot
x,y = zip(*c)
plt.plot(x,y,c='green',zorder=10)
# Plot the control points
px, py = zip(*Points)
plt.plot(px,py,'or')
a=0.5
c = CatmullRomChain(Points,a)
x,y = zip(*c)
plt.plot(x,y,c='blue')
a=1.
c = CatmullRomChain(Points,a)
x,y = zip(*c)
plt.plot(x,y,c='red')
plt.grid(b=True)
plt.show()
# In[10]:
Points
# In[ ]:
оригинальный код: https://en.wikipedia.org/wiki/Centripetal_Catmull%E2%80%93Rom_spline