Как нарисовать гладкую кривую через N точек, используя JavaScript HTML5 Canvas?
Для приложения для рисования я сохраняю координаты движения мыши в массиве, а затем рисую их с помощью lineTo. Результирующая линия не является гладкой. Как я могу создать одну кривую между всеми собранными точками?
Я гуглил, но я нашел только 3 функции для рисования линий: Для 2 точек выборки просто используйте lineTo. Для 3 точек выборки quadraticCurveTo, для 4 точек выборки bezierCurveTo.
(Я попытался нарисовать bezierCurveTo для каждых 4 точек в массиве, но это приводит к перегибам каждые 4 точки выборки вместо непрерывной плавной кривой.)
Как мне написать функцию для рисования гладкой кривой с 5 точками выборки и выше?
14 ответов
Проблема с соединением последующих точек выборки с непересекающимися функциями типа "curveTo" заключается в том, что место, где встречаются кривые, не является гладким. Это потому, что две кривые имеют общую конечную точку, но находятся под влиянием совершенно непересекающихся контрольных точек. Одним из решений является "изгиб к" средним точкам между следующими 2 последующими точками выборки. Объединение кривых с использованием этих новых интерполированных точек дает плавный переход в конечных точках (то, что является конечной точкой для одной итерации, становится контрольной точкой для следующей итерации). Другими словами, две несвязанные кривые теперь имеют гораздо больше общего.
Это решение было извлечено из книги "Основы анимации ActionScript 3.0: заставить вещи двигаться". с.95 - техника рендеринга: создание нескольких кривых.
Примечание: это решение фактически рисует не каждую из точек, которая была названием моего вопроса (скорее оно аппроксимирует кривую через точки выборки, но никогда не проходит через точки выборки), но для моих целей (приложение для рисования), это достаточно хорошо для меня, и визуально вы не можете увидеть разницу. Существует решение для прохождения всех точек выборки, но оно намного сложнее (см. http://www.cartogrammar.com/blog/actionscript-curves-update/).
Вот чертежный код для метода приближения:
// move to the first point
ctx.moveTo(points[0].x, points[0].y);
for (i = 1; i < points.length - 2; i ++)
{
var xc = (points[i].x + points[i + 1].x) / 2;
var yc = (points[i].y + points[i + 1].y) / 2;
ctx.quadraticCurveTo(points[i].x, points[i].y, xc, yc);
}
// curve through the last two points
ctx.quadraticCurveTo(points[i].x, points[i].y, points[i+1].x,points[i+1].y);
Немного поздно, но для записи.
Вы можете добиться плавных линий, используя кардинальные сплайны (или канонический сплайн), чтобы рисовать плавные кривые, проходящие через точки.
Я сделал эту функцию для холста - она разделена на три функции для повышения универсальности. Основная функция-обертка выглядит так:
function drawCurve(ctx, ptsa, tension, isClosed, numOfSegments, showPoints) {
showPoints = showPoints ? showPoints : false;
ctx.beginPath();
drawLines(ctx, getCurvePoints(ptsa, tension, isClosed, numOfSegments));
if (showPoints) {
ctx.stroke();
ctx.beginPath();
for(var i=0;i<ptsa.length-1;i+=2)
ctx.rect(ptsa[i] - 2, ptsa[i+1] - 2, 4, 4);
}
}
Чтобы нарисовать кривую, нужно иметь массив с точками x, y в следующем порядке: x1,y1, x2,y2, ...xn,yn,
Используйте это так:
var myPoints = [10,10, 40,30, 100,10]; //minimum two points
var tension = 1;
drawCurve(ctx, myPoints); //default tension=0.5
drawCurve(ctx, myPoints, tension);
Вышеприведенная функция вызывает две подфункции, одну для вычисления сглаженных точек. Это возвращает массив с новыми точками - это основная функция, которая вычисляет сглаженные точки:
function getCurvePoints(pts, tension, isClosed, numOfSegments) {
// use input value if provided, or use a default value
tension = (typeof tension != 'undefined') ? tension : 0.5;
isClosed = isClosed ? isClosed : false;
numOfSegments = numOfSegments ? numOfSegments : 16;
var _pts = [], res = [], // clone array
x, y, // our x,y coords
t1x, t2x, t1y, t2y, // tension vectors
c1, c2, c3, c4, // cardinal points
st, t, i; // steps based on num. of segments
// clone array so we don't change the original
//
_pts = pts.slice(0);
// The algorithm require a previous and next point to the actual point array.
// Check if we will draw closed or open curve.
// If closed, copy end points to beginning and first points to end
// If open, duplicate first points to befinning, end points to end
if (isClosed) {
_pts.unshift(pts[pts.length - 1]);
_pts.unshift(pts[pts.length - 2]);
_pts.unshift(pts[pts.length - 1]);
_pts.unshift(pts[pts.length - 2]);
_pts.push(pts[0]);
_pts.push(pts[1]);
}
else {
_pts.unshift(pts[1]); //copy 1. point and insert at beginning
_pts.unshift(pts[0]);
_pts.push(pts[pts.length - 2]); //copy last point and append
_pts.push(pts[pts.length - 1]);
}
// ok, lets start..
// 1. loop goes through point array
// 2. loop goes through each segment between the 2 pts + 1e point before and after
for (i=2; i < (_pts.length - 4); i+=2) {
for (t=0; t <= numOfSegments; t++) {
// calc tension vectors
t1x = (_pts[i+2] - _pts[i-2]) * tension;
t2x = (_pts[i+4] - _pts[i]) * tension;
t1y = (_pts[i+3] - _pts[i-1]) * tension;
t2y = (_pts[i+5] - _pts[i+1]) * tension;
// calc step
st = t / numOfSegments;
// calc cardinals
c1 = 2 * Math.pow(st, 3) - 3 * Math.pow(st, 2) + 1;
c2 = -(2 * Math.pow(st, 3)) + 3 * Math.pow(st, 2);
c3 = Math.pow(st, 3) - 2 * Math.pow(st, 2) + st;
c4 = Math.pow(st, 3) - Math.pow(st, 2);
// calc x and y cords with common control vectors
x = c1 * _pts[i] + c2 * _pts[i+2] + c3 * t1x + c4 * t2x;
y = c1 * _pts[i+1] + c2 * _pts[i+3] + c3 * t1y + c4 * t2y;
//store points in array
res.push(x);
res.push(y);
}
}
return res;
}
И чтобы на самом деле нарисовать точки в виде сглаженной кривой (или любых других сегментированных линий, если у вас есть массив x, y):
function drawLines(ctx, pts) {
ctx.moveTo(pts[0], pts[1]);
for(i=2;i<pts.length-1;i+=2) ctx.lineTo(pts[i], pts[i+1]);
}
var ctx = document.getElementById("c").getContext("2d");
function drawCurve(ctx, ptsa, tension, isClosed, numOfSegments, showPoints) {
ctx.beginPath();
drawLines(ctx, getCurvePoints(ptsa, tension, isClosed, numOfSegments));
if (showPoints) {
ctx.beginPath();
for(var i=0;i<ptsa.length-1;i+=2)
ctx.rect(ptsa[i] - 2, ptsa[i+1] - 2, 4, 4);
}
ctx.stroke();
}
var myPoints = [10,10, 40,30, 100,10, 200, 100, 200, 50, 250, 120]; //minimum two points
var tension = 1;
drawCurve(ctx, myPoints); //default tension=0.5
drawCurve(ctx, myPoints, tension);
function getCurvePoints(pts, tension, isClosed, numOfSegments) {
// use input value if provided, or use a default value
tension = (typeof tension != 'undefined') ? tension : 0.5;
isClosed = isClosed ? isClosed : false;
numOfSegments = numOfSegments ? numOfSegments : 16;
var _pts = [], res = [], // clone array
x, y, // our x,y coords
t1x, t2x, t1y, t2y, // tension vectors
c1, c2, c3, c4, // cardinal points
st, t, i; // steps based on num. of segments
// clone array so we don't change the original
//
_pts = pts.slice(0);
// The algorithm require a previous and next point to the actual point array.
// Check if we will draw closed or open curve.
// If closed, copy end points to beginning and first points to end
// If open, duplicate first points to befinning, end points to end
if (isClosed) {
_pts.unshift(pts[pts.length - 1]);
_pts.unshift(pts[pts.length - 2]);
_pts.unshift(pts[pts.length - 1]);
_pts.unshift(pts[pts.length - 2]);
_pts.push(pts[0]);
_pts.push(pts[1]);
}
else {
_pts.unshift(pts[1]); //copy 1. point and insert at beginning
_pts.unshift(pts[0]);
_pts.push(pts[pts.length - 2]); //copy last point and append
_pts.push(pts[pts.length - 1]);
}
// ok, lets start..
// 1. loop goes through point array
// 2. loop goes through each segment between the 2 pts + 1e point before and after
for (i=2; i < (_pts.length - 4); i+=2) {
for (t=0; t <= numOfSegments; t++) {
// calc tension vectors
t1x = (_pts[i+2] - _pts[i-2]) * tension;
t2x = (_pts[i+4] - _pts[i]) * tension;
t1y = (_pts[i+3] - _pts[i-1]) * tension;
t2y = (_pts[i+5] - _pts[i+1]) * tension;
// calc step
st = t / numOfSegments;
// calc cardinals
c1 = 2 * Math.pow(st, 3) - 3 * Math.pow(st, 2) + 1;
c2 = -(2 * Math.pow(st, 3)) + 3 * Math.pow(st, 2);
c3 = Math.pow(st, 3) - 2 * Math.pow(st, 2) + st;
c4 = Math.pow(st, 3) - Math.pow(st, 2);
// calc x and y cords with common control vectors
x = c1 * _pts[i] + c2 * _pts[i+2] + c3 * t1x + c4 * t2x;
y = c1 * _pts[i+1] + c2 * _pts[i+3] + c3 * t1y + c4 * t2y;
//store points in array
res.push(x);
res.push(y);
}
}
return res;
}
function drawLines(ctx, pts) {
ctx.moveTo(pts[0], pts[1]);
for(i=2;i<pts.length-1;i+=2) ctx.lineTo(pts[i], pts[i+1]);
}canvas { border: 1px solid red; }<canvas id="c"><canvas>Это приводит к этому:
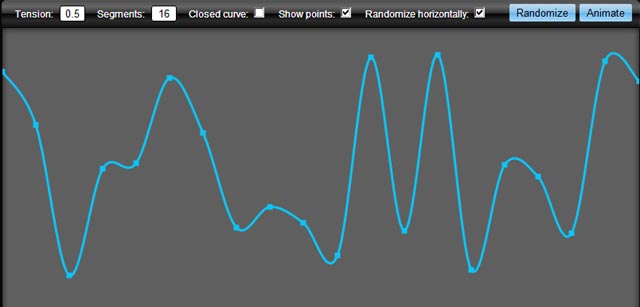
Вы можете легко расширить холст, чтобы вместо этого называть его так:
ctx.drawCurve(myPoints);
Добавьте следующее в JavaScript:
if (CanvasRenderingContext2D != 'undefined') {
CanvasRenderingContext2D.prototype.drawCurve =
function(pts, tension, isClosed, numOfSegments, showPoints) {
drawCurve(this, pts, tension, isClosed, numOfSegments, showPoints)}
}
Вы можете найти более оптимизированную версию этого на NPM (npm i cardinal-spline-js) или на GitLab.
Первый ответ не пройдет через все пункты. Этот график будет точно проходить через все точки и будет представлять собой кривую префекта с точками в виде точек как [{x:,y:}] n таких точек.
var points = [{x:1,y:1},{x:2,y:3},{x:3,y:4},{x:4,y:2},{x:5,y:6}] //took 5 example points
ctx.moveTo((points[0].x), points[0].y);
for(var i = 0; i < points.length-1; i ++)
{
var x_mid = (points[i].x + points[i+1].x) / 2;
var y_mid = (points[i].y + points[i+1].y) / 2;
var cp_x1 = (x_mid + points[i].x) / 2;
var cp_x2 = (x_mid + points[i+1].x) / 2;
ctx.quadraticCurveTo(cp_x1,points[i].y ,x_mid, y_mid);
ctx.quadraticCurveTo(cp_x2,points[i+1].y ,points[i+1].x,points[i+1].y);
}
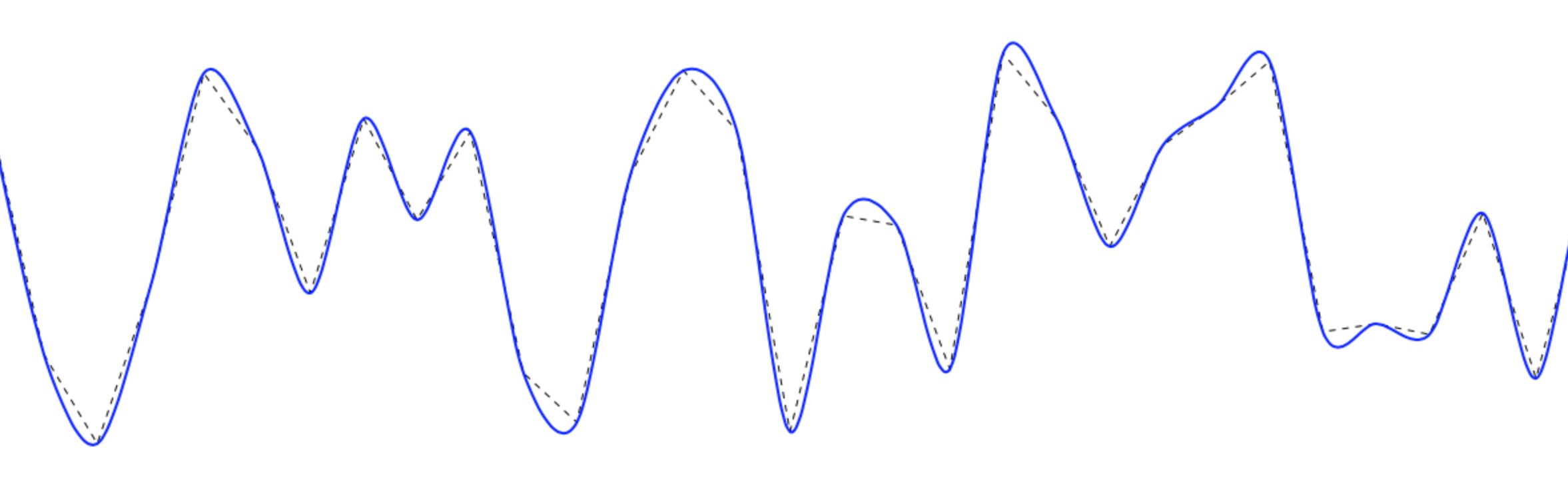
Я решил добавить, а не публиковать свое решение в другой публикации. Ниже приведено решение, которое я создаю, может быть не идеальным, но пока результат хороший.
Важно: оно пройдет через все точки!
Если у вас есть идеи, чтобы сделать это лучше, пожалуйста, поделитесь со мной. Благодарю.
Вот сравнение до после:
Сохраните этот код в HTML, чтобы проверить это.
<!DOCTYPE html>
<html>
<body>
<canvas id="myCanvas" width="1200" height="700" style="border:1px solid #d3d3d3;">Your browser does not support the HTML5 canvas tag.</canvas>
<script>
var cv = document.getElementById("myCanvas");
var ctx = cv.getContext("2d");
function gradient(a, b) {
return (b.y-a.y)/(b.x-a.x);
}
function bzCurve(points, f, t) {
//f = 0, will be straight line
//t suppose to be 1, but changing the value can control the smoothness too
if (typeof(f) == 'undefined') f = 0.3;
if (typeof(t) == 'undefined') t = 0.6;
ctx.beginPath();
ctx.moveTo(points[0].x, points[0].y);
var m = 0;
var dx1 = 0;
var dy1 = 0;
var preP = points[0];
for (var i = 1; i < points.length; i++) {
var curP = points[i];
nexP = points[i + 1];
if (nexP) {
m = gradient(preP, nexP);
dx2 = (nexP.x - curP.x) * -f;
dy2 = dx2 * m * t;
} else {
dx2 = 0;
dy2 = 0;
}
ctx.bezierCurveTo(preP.x - dx1, preP.y - dy1, curP.x + dx2, curP.y + dy2, curP.x, curP.y);
dx1 = dx2;
dy1 = dy2;
preP = curP;
}
ctx.stroke();
}
// Generate random data
var lines = [];
var X = 10;
var t = 40; //to control width of X
for (var i = 0; i < 100; i++ ) {
Y = Math.floor((Math.random() * 300) + 50);
p = { x: X, y: Y };
lines.push(p);
X = X + t;
}
//draw straight line
ctx.beginPath();
ctx.setLineDash([5]);
ctx.lineWidth = 1;
bzCurve(lines, 0, 1);
//draw smooth line
ctx.setLineDash([0]);
ctx.lineWidth = 2;
ctx.strokeStyle = "blue";
bzCurve(lines, 0.3, 1);
</script>
</body>
</html>
Как указывает Дэниел Ховард, Роб Спенсер описывает то, что вы хотите, по адресу http://scaledinnovation.com/analytics/splines/aboutSplines.html.
Вот интерактивная демонстрация: http://jsbin.com/ApitIxo/2/
Это фрагмент кода на случай, если jsbin не работает.
<!DOCTYPE html>
<html>
<head>
<meta charset=utf-8 />
<title>Demo smooth connection</title>
</head>
<body>
<div id="display">
Click to build a smooth path.
(See Rob Spencer's <a href="http://scaledinnovation.com/analytics/splines/aboutSplines.html">article</a>)
<br><label><input type="checkbox" id="showPoints" checked> Show points</label>
<br><label><input type="checkbox" id="showControlLines" checked> Show control lines</label>
<br>
<label>
<input type="range" id="tension" min="-1" max="2" step=".1" value=".5" > Tension <span id="tensionvalue">(0.5)</span>
</label>
<div id="mouse"></div>
</div>
<canvas id="canvas"></canvas>
<style>
html { position: relative; height: 100%; width: 100%; }
body { position: absolute; left: 0; right: 0; top: 0; bottom: 0; }
canvas { outline: 1px solid red; }
#display { position: fixed; margin: 8px; background: white; z-index: 1; }
</style>
<script>
function update() {
$("tensionvalue").innerHTML="("+$("tension").value+")";
drawSplines();
}
$("showPoints").onchange = $("showControlLines").onchange = $("tension").onchange = update;
// utility function
function $(id){ return document.getElementById(id); }
var canvas=$("canvas"), ctx=canvas.getContext("2d");
function setCanvasSize() {
canvas.width = parseInt(window.getComputedStyle(document.body).width);
canvas.height = parseInt(window.getComputedStyle(document.body).height);
}
window.onload = window.onresize = setCanvasSize();
function mousePositionOnCanvas(e) {
var el=e.target, c=el;
var scaleX = c.width/c.offsetWidth || 1;
var scaleY = c.height/c.offsetHeight || 1;
if (!isNaN(e.offsetX))
return { x:e.offsetX*scaleX, y:e.offsetY*scaleY };
var x=e.pageX, y=e.pageY;
do {
x -= el.offsetLeft;
y -= el.offsetTop;
el = el.offsetParent;
} while (el);
return { x: x*scaleX, y: y*scaleY };
}
canvas.onclick = function(e){
var p = mousePositionOnCanvas(e);
addSplinePoint(p.x, p.y);
};
function drawPoint(x,y,color){
ctx.save();
ctx.fillStyle=color;
ctx.beginPath();
ctx.arc(x,y,3,0,2*Math.PI);
ctx.fill()
ctx.restore();
}
canvas.onmousemove = function(e) {
var p = mousePositionOnCanvas(e);
$("mouse").innerHTML = p.x+","+p.y;
};
var pts=[]; // a list of x and ys
// given an array of x,y's, return distance between any two,
// note that i and j are indexes to the points, not directly into the array.
function dista(arr, i, j) {
return Math.sqrt(Math.pow(arr[2*i]-arr[2*j], 2) + Math.pow(arr[2*i+1]-arr[2*j+1], 2));
}
// return vector from i to j where i and j are indexes pointing into an array of points.
function va(arr, i, j){
return [arr[2*j]-arr[2*i], arr[2*j+1]-arr[2*i+1]]
}
function ctlpts(x1,y1,x2,y2,x3,y3) {
var t = $("tension").value;
var v = va(arguments, 0, 2);
var d01 = dista(arguments, 0, 1);
var d12 = dista(arguments, 1, 2);
var d012 = d01 + d12;
return [x2 - v[0] * t * d01 / d012, y2 - v[1] * t * d01 / d012,
x2 + v[0] * t * d12 / d012, y2 + v[1] * t * d12 / d012 ];
}
function addSplinePoint(x, y){
pts.push(x); pts.push(y);
drawSplines();
}
function drawSplines() {
clear();
cps = []; // There will be two control points for each "middle" point, 1 ... len-2e
for (var i = 0; i < pts.length - 2; i += 1) {
cps = cps.concat(ctlpts(pts[2*i], pts[2*i+1],
pts[2*i+2], pts[2*i+3],
pts[2*i+4], pts[2*i+5]));
}
if ($("showControlLines").checked) drawControlPoints(cps);
if ($("showPoints").checked) drawPoints(pts);
drawCurvedPath(cps, pts);
}
function drawControlPoints(cps) {
for (var i = 0; i < cps.length; i += 4) {
showPt(cps[i], cps[i+1], "pink");
showPt(cps[i+2], cps[i+3], "pink");
drawLine(cps[i], cps[i+1], cps[i+2], cps[i+3], "pink");
}
}
function drawPoints(pts) {
for (var i = 0; i < pts.length; i += 2) {
showPt(pts[i], pts[i+1], "black");
}
}
function drawCurvedPath(cps, pts){
var len = pts.length / 2; // number of points
if (len < 2) return;
if (len == 2) {
ctx.beginPath();
ctx.moveTo(pts[0], pts[1]);
ctx.lineTo(pts[2], pts[3]);
ctx.stroke();
}
else {
ctx.beginPath();
ctx.moveTo(pts[0], pts[1]);
// from point 0 to point 1 is a quadratic
ctx.quadraticCurveTo(cps[0], cps[1], pts[2], pts[3]);
// for all middle points, connect with bezier
for (var i = 2; i < len-1; i += 1) {
// console.log("to", pts[2*i], pts[2*i+1]);
ctx.bezierCurveTo(
cps[(2*(i-1)-1)*2], cps[(2*(i-1)-1)*2+1],
cps[(2*(i-1))*2], cps[(2*(i-1))*2+1],
pts[i*2], pts[i*2+1]);
}
ctx.quadraticCurveTo(
cps[(2*(i-1)-1)*2], cps[(2*(i-1)-1)*2+1],
pts[i*2], pts[i*2+1]);
ctx.stroke();
}
}
function clear() {
ctx.save();
// use alpha to fade out
ctx.fillStyle = "rgba(255,255,255,.7)"; // clear screen
ctx.fillRect(0,0,canvas.width,canvas.height);
ctx.restore();
}
function showPt(x,y,fillStyle) {
ctx.save();
ctx.beginPath();
if (fillStyle) {
ctx.fillStyle = fillStyle;
}
ctx.arc(x, y, 5, 0, 2*Math.PI);
ctx.fill();
ctx.restore();
}
function drawLine(x1, y1, x2, y2, strokeStyle){
ctx.beginPath();
ctx.moveTo(x1, y1);
ctx.lineTo(x2, y2);
if (strokeStyle) {
ctx.save();
ctx.strokeStyle = strokeStyle;
ctx.stroke();
ctx.restore();
}
else {
ctx.save();
ctx.strokeStyle = "pink";
ctx.stroke();
ctx.restore();
}
}
</script>
</body>
</html>Я нашел это работать хорошо
function drawCurve(points, tension) {
ctx.beginPath();
ctx.moveTo(points[0].x, points[0].y);
var t = (tension != null) ? tension : 1;
for (var i = 0; i < points.length - 1; i++) {
var p0 = (i > 0) ? points[i - 1] : points[0];
var p1 = points[i];
var p2 = points[i + 1];
var p3 = (i != points.length - 2) ? points[i + 2] : p2;
var cp1x = p1.x + (p2.x - p0.x) / 6 * t;
var cp1y = p1.y + (p2.y - p0.y) / 6 * t;
var cp2x = p2.x - (p3.x - p1.x) / 6 * t;
var cp2y = p2.y - (p3.y - p1.y) / 6 * t;
ctx.bezierCurveTo(cp1x, cp1y, cp2x, cp2y, p2.x, p2.y);
}
ctx.stroke();
}
Попробуйте KineticJS - вы можете определить сплайн с массивом точек. Вот пример:
Старый URL: http://www.html5canvastutorials.com/kineticjs/html5-canvas-kineticjs-spline-tutorial/
Bonjour
Я ценю решение user1693593: полиномы Эрмита кажутся лучшим способом контролировать то, что будет нарисовано, и наиболее удовлетворительным с математической точки зрения. Тема вроде бы давно закрыта, но, может быть, некоторым опоздавшим, вроде меня, она все еще интересна. Я искал бесплатный интерактивный конструктор сюжетов, который позволил бы мне сохранить кривую и повторно использовать ее где-нибудь еще, но не нашел ничего подобного в Интернете: поэтому я сделал это по-своему, из источника в Википедии. упомянул user1693593. Здесь сложно объяснить, как это работает, и лучший способ узнать, стоит ли это делать, - это посмотреть https://sites.google.com/view/divertissements/accueil/splines.
Невероятно поздно, но вдохновленный блестяще простым ответом Хомана, позвольте мне опубликовать более общее решение (общее в том смысле, что решение Хомана дает сбой на массивах точек с менее чем 3 вершинами):
function smooth(ctx, points)
{
if(points == undefined || points.length == 0)
{
return true;
}
if(points.length == 1)
{
ctx.moveTo(points[0].x, points[0].y);
ctx.lineTo(points[0].x, points[0].y);
return true;
}
if(points.length == 2)
{
ctx.moveTo(points[0].x, points[0].y);
ctx.lineTo(points[1].x, points[1].y);
return true;
}
ctx.moveTo(points[0].x, points[0].y);
for (var i = 1; i < points.length - 2; i ++)
{
var xc = (points[i].x + points[i + 1].x) / 2;
var yc = (points[i].y + points[i + 1].y) / 2;
ctx.quadraticCurveTo(points[i].x, points[i].y, xc, yc);
}
ctx.quadraticCurveTo(points[i].x, points[i].y, points[i+1].x, points[i+1].y);
}
Этот код мне идеально подходит:
this.context.beginPath();
this.context.moveTo(data[0].x, data[0].y);
for (let i = 1; i < data.length; i++) {
this.context.bezierCurveTo(
data[i - 1].x + (data[i].x - data[i - 1].x) / 2,
data[i - 1].y,
data[i - 1].x + (data[i].x - data[i - 1].x) / 2,
data[i].y,
data[i].x,
data[i].y);
}
у вас правильная плавная линия и правильные конечные точки ВНИМАНИЕ! (y = "высота холста" - y);
Несколько иной ответ на исходный вопрос;
Если кто-то хочет нарисовать фигуру:
- что описывается серией точек
- где линия имеет небольшую кривую в точках
- линия не обязательно должна проходить через точки (т.е. проходит немного «внутрь» из них)
Тогда, надеюсь, моя функция ниже может помочь
Мне как-то нужен способ, который использует только квадратичный Безье. Это мой метод, и его можно распространить на 3d:
Формула четырехъядерной кривой Безье:
b(t) = (1-t)^2A + 2(1-t) tB + t^2*C
Когда t = 0 или 1, кривая может проходить через точку A или C, но не обязательно проходит через точку B.
Его производная первого порядка равна
b'(t) = 2(t-1)A + 2(1-2 t) B + 2 t C
Чтобы построить кривую, проходящую через точки P0,P1,P2 с двумя четверными кривыми Безье, наклоны двух кривых Безье в точке p1 должны быть равны
b'α(t) = 2(t-1)P0 + 2(1-2 t) M1 + 2 t P1
b'β(t) = 2(t-1)P1 + 2(1-2 t) M2 + 2 t P2
б'α(1) = б'β(0)
Это дает
(М1 + М2) / 2 = П1
Итак, кривую через 3 точки можно нарисовать вот так
bezier(p0, m1, p1);
bezier(p1, m2, p2);
Где . Направлениеm1m2не имеет значения, можно найти поp2 - p1.
Для кривых, проходящих через 4 и более точек
bezier(p0, m1, p1);
bezier(p1, m2, (m2 + m3) / 2);
bezier((m2 + m3) / 2, m3, p2);
bezier(p2, m4, p3);
Гдеm1p1 = p1m2иm3p2 = p2m4.
function drawCurve(ctx: CanvasRenderingContext2D, points: { x: number, y: number }[], tension = 2) {
if (points.length < 2) {
return;
}
ctx.beginPath();
if (points.length === 2) {
ctx.moveTo(points[0].x, points[0].y);
ctx.lineTo(points[1].x, points[1].y);
ctx.stroke();
return;
}
let prevM2x = 0;
let prevM2y = 0;
for (let i = 1, len = points.length; i < len - 1; ++i) {
const p0 = points[i - 1];
const p1 = points[i];
const p2 = points[i + 1];
let tx = p2.x - (i === 1 ? p0.x : prevM2x);
let ty = p2.y - (i === 1 ? p0.y : prevM2y);
const tLen = Math.sqrt(tx ** 2 + ty ** 2);
if (tLen > 1e-8) {
const inv = 1 / tLen;
tx *= inv;
ty *= inv;
} else {
tx = 0;
ty = 0;
}
const det = Math.sqrt(Math.min(
(p0.x - p1.x) ** 2 + (p0.y - p1.y) ** 2,
(p2.x - p1.x) ** 2 + (p2.y - p1.y) ** 2
)) / (2 * tension);
const m1x = p1.x - tx * det;
const m1y = p1.y - ty * det;
const m2x = p1.x + tx * det;
const m2y = p1.y + ty * det;
if (i === 1) {
ctx.moveTo(p0.x, p0.y);
ctx.quadraticCurveTo(m1x, m1y, p1.x, p1.y);
} else {
const mx = (prevM2x + m1x) / 2;
const my = (prevM2y + m1y) / 2;
ctx.quadraticCurveTo(prevM2x, prevM2y, mx, my);
ctx.quadraticCurveTo(m1x, m1y, p1.x, p1.y);
}
if (i === len - 2) {
ctx.quadraticCurveTo(m2x, m2y, p2.x, p2.y);
}
prevM2x = m2x;
prevM2y = m2y;
}
ctx.stroke();
}
Если вы хотите определить уравнение кривой через n точек, следующий код предоставит вам коэффициенты полинома степени n-1 и сохранит эти коэффициенты в coefficients[]массив (начиная с постоянного члена). Координаты x не обязательно должны быть в порядке. Это пример полинома Лагранжа.
var xPoints=[2,4,3,6,7,10]; //example coordinates
var yPoints=[2,5,-2,0,2,8];
var coefficients=[];
for (var m=0; m<xPoints.length; m++) coefficients[m]=0;
for (var m=0; m<xPoints.length; m++) {
var newCoefficients=[];
for (var nc=0; nc<xPoints.length; nc++) newCoefficients[nc]=0;
if (m>0) {
newCoefficients[0]=-xPoints[0]/(xPoints[m]-xPoints[0]);
newCoefficients[1]=1/(xPoints[m]-xPoints[0]);
} else {
newCoefficients[0]=-xPoints[1]/(xPoints[m]-xPoints[1]);
newCoefficients[1]=1/(xPoints[m]-xPoints[1]);
}
var startIndex=1;
if (m==0) startIndex=2;
for (var n=startIndex; n<xPoints.length; n++) {
if (m==n) continue;
for (var nc=xPoints.length-1; nc>=1; nc--) {
newCoefficients[nc]=newCoefficients[nc]*(-xPoints[n]/(xPoints[m]-xPoints[n]))+newCoefficients[nc-1]/(xPoints[m]-xPoints[n]);
}
newCoefficients[0]=newCoefficients[0]*(-xPoints[n]/(xPoints[m]-xPoints[n]));
}
for (var nc=0; nc<xPoints.length; nc++) coefficients[nc]+=yPoints[m]*newCoefficients[nc];
}
Чтобы добавить к кардинальному методу сплайнов в K3N и, возможно, решить озабоченность Т. Дж. Краудера по поводу "наклонов" кривых в вводящих в заблуждение местах, я вставил следующий код в getCurvePoints() функция, как раз перед res.push(x);
if ((y < _pts[i+1] && y < _pts[i+3]) || (y > _pts[i+1] && y > _pts[i+3])) {
y = (_pts[i+1] + _pts[i+3]) / 2;
}
if ((x < _pts[i] && x < _pts[i+2]) || (x > _pts[i] && x > _pts[i+2])) {
x = (_pts[i] + _pts[i+2]) / 2;
}
Это эффективно создает (невидимый) ограничивающий прямоугольник между каждой парой последовательных точек и гарантирует, что кривая остается в этом ограничивающем прямоугольнике - т.е. если точка на кривой находится выше / ниже / влево / вправо от обеих точек, она меняет свое положение, чтобы оказаться внутри рамки. Здесь используется средняя точка, но это можно улучшить, возможно, используя линейную интерполяцию.