Возникла небольшая проблема с вычислением радиуса ограничивающей сферы

Question

Мне удалось рассчитать радиус ограничивающей сферы двумя способами, но ни один не дает мне именно то, что я хочу. Мне не нужна "пиксельная" идеальная ограничивающая сфера, но я бы хотел что-то лучше, чем то, что у меня есть в настоящее время.

Я использую модели Wavefront .obj и для вычисления радиуса ограничивающей сферы для этих моделей я извлекаю размеры текущей модели (я использую библиотеку GLM от Нейта Роббинса), которая даст мне размер по каждой оси.

Первый подход: разделите каждую ось на 2, и это даст мне радиус на каждой оси. Самый большой - тот, который я буду использовать для моей ограничивающей сферы. Это будет работать для большинства объектов, характерных для моего проекта. Это не будет работать для некоторых, как кубовидные. По сути, если у меня есть куб и я рассчитал радиус с этим подходом, сфера оставит углы куба снаружи.

Второй подход: разделите каждую ось на 2, и это даст мне радиус на каждой оси. Затем я делаю это, чтобы вывести радиус для ограничивающей сферы:

r = SQRT(x*x + y*y + z*z)

Но это дает мне довольно большой радиус. Объект будет полностью заключен в сферу, но сфера довольно большая, больше, чем должна быть.

Я не понимаю, что я делаю неправильно в формуле выше, насколько я знаю, это должно работать. Но я явно ошибаюсь...

Answer 1

Ваш второй подход должен дать вам ограничивающую сферу для вашей ограничительной рамки, но, как вы обнаружили, она будет больше, чем необходимо для чего-либо, кроме рамки.

Лучшую ограничивающую сферу можно найти, переместив точки модели так, чтобы они центрировались на начале координат, используя уже имеющиеся размеры ограничивающего прямоугольника, а затем для каждой отдельной вершины вычислите радиус от начала координат для этой точки, используя sqrt(x*x + y*y + z*z) формула. Какой из них является самым большим, это радиус вашей ограничивающей сферы.

Обратите внимание, что это не будет оптимальной ограничивающей сферой. Для этого вам нужно найти выпуклый корпус вашей модели и использовать что-то вроде вращающихся штангенциркулей, чтобы выбрать оптимальную центральную точку для сферы.

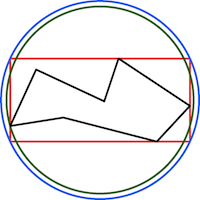
Чтобы показать его в 2D, красный контур - ограничивающий прямоугольник формы, а синий круг - ограничивающий круг прямоугольника. Улучшенный круг, использующий вершины многоугольника и центрированный на прямоугольнике, имеет зеленый цвет. Обратите внимание, что ни одна из точек черного многоугольника не касается синего круга.

Answer 2

Одним простым способом было бы использовать Miniball для вычисления точной ограничивающей сферы модели. Интеграция его в ваш проект без проблем, так как он состоит только из одного заголовка. Однако он лицензирован по лицензии GPL, что может быть проблемой. Пример:

#include "Miniball.h"

// ...

Miniball<3> boundingSphere;

// Iterate over all vertices in the model
for (int vertexId = 0; vertexId < model.getNumVertices(); ++vertexId) {
  // Convert vertex position to Miniball point type
  Point<3> point;
  for (int dim = 0; dim < 3; ++dim) {
    point[dim] = model.getVertex(vertexId)[dim];
  }
  // Add point to bounding sphere
  boundingSphere.check_in(point);
}
// Actually calculate the sphere
boundingSphere.build();

// Get back the results
Point<3> center = boundingSphere.center();
double radiusSq = boundingSphere.squared_radius();

Answer 3

Если это сфера, то разве вам не нужно обрабатывать ее только по одной оси? Я мог бы быть далеко отсюда - но по определению, сфера не будет иметь такую ​​же ширину, высоту и глубину? Так радиус на одной оси = радиус на другой = радиус другого?