Шестиугольные сетки, как вы находите, в каком шестиугольнике находится точка?
У меня есть карта, состоящая из строк и столбцов шестиугольников
Это не реальное изображение гекс-карты, которую я использую, но использует шестиугольники того же размера и формы
Мне нужно знать, над какой мышью щелкает пользователь,
Каждый шестиугольник представлен экземпляром класса "Плитка", однако он не содержит никаких данных, специфичных для местоположения, или даже многоугольника, поэтому, по сути, единственный способ узнать, где находится конкретный шестиугольник, это узнать его положение в 2D массив.
Я использовал квадратную сетку раньше, и было довольно легко выяснить, какой квадрат был выбран, потому что пиксели также квадратные,
// example where each square is 10 by 10 pixels:
private void getClickedSquare(MouseEvent me)
{
int mouseX = me.getX();// e.g. 25
int mouseY = me.getY();// e.g. 70
int squareX= (int) (mouseX / 10);// in this case 2
int squareY= (int) (mouseY / 10);// in this case 7
//then to access the tile I would do
map.squares[squareX][squareY].whatever();
}
Но я даже не уверен, с чего начать с шестиугольников, у кого-нибудь есть опыт?
Я не могу использовать полигоны (Java), так как, когда я начинаю перемещать карту по экрану и увеличивать ее размер, у меня возникают проблемы с обновлением огромного количества полигонов в каждом кадре. Хотя тогда я мог бы просто проверить, включена ли точка в любой из полигонов тайла карты!
На данный момент отображаемые шестиугольники являются просто BufferedImages.
Если вы хотите узнать больше информации, пожалуйста, спросите, спасибо за ваше время:D
9 ответов
(ОБНОВЛЕНО: переработан код, чтобы сделать его более понятным и эффективным) (ОБНОВЛЕНО: уменьшена длина ответа, исправлены ошибки в коде, улучшено качество изображений)
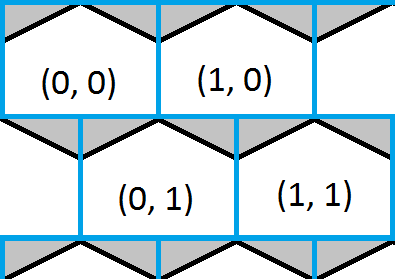
Это изображение показывает верхний левый угол гексагональной сетки и наложена синяя квадратная сетка. Легко определить, какой из квадратов находится внутри, и это дало бы грубое приближение к какому шестиугольнику тоже. Белые части шестиугольников показывают, где квадрат и шестиугольная сетка имеют одинаковые координаты, а серые части шестиугольников показывают, где их нет.
Решение теперь так же просто, как найти, в каком поле находится точка, затем проверить, находится ли точка в каком-либо из треугольников, и скорректировать ответ, если это необходимо.
private final Hexagon getSelectedHexagon(int x, int y)
{
// Find the row and column of the box that the point falls in.
int row = (int) (y / gridHeight);
int column;
boolean rowIsOdd = row % 2 == 1;
// Is the row an odd number?
if (rowIsOdd)// Yes: Offset x to match the indent of the row
column = (int) ((x - halfWidth) / gridWidth);
else// No: Calculate normally
column = (int) (x / gridWidth);
В этой точке у нас есть строка и столбец прямоугольника, в котором находится наша точка, затем нам нужно проверить нашу точку на двух верхних краях шестиугольника, чтобы увидеть, находится ли наша точка в каком-либо из шестиугольников выше:
// Work out the position of the point relative to the box it is in
double relY = y - (row * gridHeight);
double relX;
if (rowIsOdd)
relX = (x - (column * gridWidth)) - halfWidth;
else
relX = x - (column * gridWidth);
Наличие относительных координат облегчает следующий шаг.
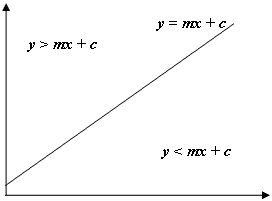
Как и на рисунке выше, если у нашей точки > mx + c, мы знаем, что наша точка лежит над линией, а в нашем случае - шестиугольником выше и слева от текущей строки и столбца. Обратите внимание, что система координат в java имеет y, начинающуюся с 0 в верхнем левом углу экрана, а не нижний левый, как обычно в математике, следовательно, отрицательный градиент, используемый для левого края, и положительный градиент, используемый для правой.
// Work out if the point is above either of the hexagon's top edges
if (relY < (-m * relX) + c) // LEFT edge
{
row--;
if (!rowIsOdd)
column--;
}
else if (relY < (m * relX) - c) // RIGHT edge
{
row--;
if (rowIsOdd)
column++;
}
return hexagons[column][row];
}
Краткое объяснение переменных, использованных в приведенном выше примере:
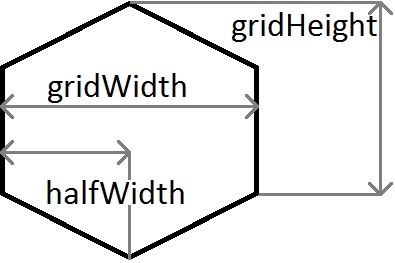
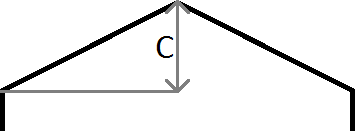
m - градиент, поэтому m = c / halfWidth
РЕДАКТИРОВАТЬ: этот вопрос сложнее, чем я думал сначала, я перепишу свой ответ с некоторыми рабочими, однако я не уверен, является ли путь решения каким-либо улучшением других ответов.
Вопрос можно перефразировать: для любого x, y найдите шестиугольник, центр которого ближе всего к x, y
то есть минимизировать dist_squared (Hex [n].center, (x, y)) над n (в квадрате означает, что вам не нужно беспокоиться о квадратных корнях, которые экономят некоторый процессор)
Однако сначала мы должны сузить число шестиугольников для проверки - мы можем сузить его максимум до 5 следующим способом:
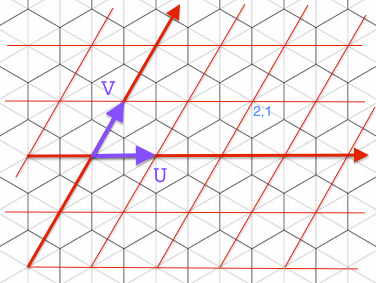
Итак, первый шаг - Выразите свою точку (x, y) в УФ-пространстве, т.е. (x,y) = лямбдаU + mu V, поэтому = (лямбда, mu) в УФ-пространстве
Это всего лишь двухмерное матричное преобразование ( http://playtechs.blogspot.co.uk/2007/04/hex-grids.html может быть полезным, если вы не понимаете линейные преобразования).
Теперь с учетом точки (лямбда, мю), если мы округляем оба до ближайшего целого числа, то имеем:
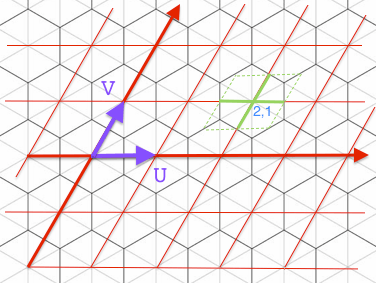
Везде в пределах Зеленого квадрата карты обратно к (2,1)
Таким образом, большинство точек в этом зеленом квадрате будут правильными, т.е. они находятся в шестиугольнике (2,1).
Но некоторые точки должны возвращать шестиугольник # (2,2), то есть:
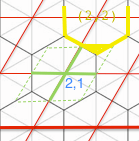
Точно так же некоторые должны возвращать шестиугольник # (3,1). И затем в противоположном углу этого зеленого параллелограмма будут еще 2 области.
Итак, подведем итог: если int(lambda,mu) = (p,q), то мы, вероятно, находимся внутри шестиугольника (p, q), но мы также можем быть внутри шестиугольников (p+1,q), (p,q+1), (p-1,q) или (p,q-1)
Несколько способов определить, какой из них имеет место. Проще всего было бы преобразовать центры всех этих пяти шестиугольников обратно в исходную систему координат и найти ближайшую к нашей точке.
Но оказывается, что вы можете сузить это до ~50% времени, не делая проверки расстояния, ~25% времени делая одну проверку расстояния, а оставшиеся ~ 25% времени, делая 2 проверки расстояния (я предполагаю, цифры, глядя на области, на которых работает каждая проверка):
p,q = int(lambda,mu)
if lambda * mu < 0.0:
// opposite signs, so we are guaranteed to be inside hexagon (p,q)
// look at the picture to understand why; we will be in the green regions
outPQ = p,q

else:
// circle check
distSquared = dist2( Hex2Rect(p,q), Hex2Rect(lambda, mu) )
if distSquared < .5^2:
// inside circle, so guaranteed inside hexagon (p,q)
outPQ = p,q
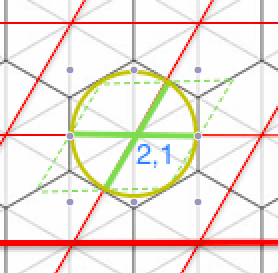
else:
if lambda > 0.0:
candHex = (lambda>mu) ? (p+1,q): (p,q+1)
else:
candHex = (lambda<mu) ? (p-1,q) : (p,q-1)
И этот последний тест можно привести в порядок:
else:
// same sign, but which end of the parallelogram are we?
sign = (lambda<0) ? -1 : +1
candHex = ( abs(lambda) > abs(mu) ) ? (p+sign,q) : (p,q+sign)
Теперь мы сузили его до еще одного возможного шестиугольника, нам просто нужно найти, который ближе:
dist2_cand = dist2( Hex2Rect(lambda, mu), Hex2Rect(candHex) )
outPQ = ( distSquared < dist2_cand ) ? (p,q) : candHex
Функция Dist2_hexSpace(A,B) может привести в порядок вещи.
Я начал с того, что посмотрел на ответ @pi /questions/3984091/shestiugolnyie-setki-kak-vyi-nahodite-v-kakom-shestiugolnike-nahoditsya-tochka/3984092#3984092 и подумал, что было бы интересно попробовать нечто подобное в координатах куба с UVW-пространством (а не 2D, осевое, UV-пространство).
Следующие уравнения отображают (x,y) => (u,v,w)
u = (2/3)*x;
v = -(1/3)*x + (1/2)*y;
w = -(1/3)*x - (1/2)*y;
Тогда это так же просто, как округление u, v и w до ближайшего целого числа и преобразование обратно в x, y. Однако есть большая загвоздка...
В ответе выше отмечено, что при округлении в УФ-пространстве будет несколько областей, которые отображаются неправильно:
Это также происходит при использовании кубических координат:
Любая область в оранжевых треугольниках находится на расстоянии>0,5 единиц от центра шестиугольника, а при округлении округляется в стороне от центра. Это показано выше, поскольку все, что находится в красном треугольнике (слева от линии u=1,5), будет неправильно округлено до u=1, а не до u=2.
Некоторые ключевые наблюдения здесь, хотя...
1. Оранжевые / красные проблемные области не перекрываются
2. В координатах куба действительные гекс-центры имеют u + v + w = 0
В приведенном ниже коде все u, v и w округляются с самого начала как округление только в том случае, если округленные координаты не суммируются до нуля.
uR = Math.round(u);
vR = Math.round(v);
wR = Math.round(w);
Если они не суммируются с нулем, потому что проблемные области не перекрываются, будет только 1 координата, которая будет округлена неправильно. Эта координата также является координатой, которая была округлена больше всего.
arr = [ Math.abs(u-uR), Math.abs(v-vR), Math.abs(w-wR) ];
var i = arr.indexOf(Math.max(...arr));
После того, как координата задачи найдена, она округляется в другом направлении. Итоговое значение (x, y) затем рассчитывается по округленному / скорректированному (u,v,w).
nearestHex = function(x,y){
u = (2/3)*x;
v = -(1/3)*x + (1/2)*y;
w = -(1/3)*x - (1/2)*y;
uR = Math.round(u);
vR = Math.round(v);
wR = Math.round(w);
if(uR+vR+wR !== 0){
arr = [ Math.abs(u-uR), Math.abs(v-vR), Math.abs(w-wR) ];
var i = arr.indexOf(Math.max(...arr));
switch(i){
case 0:
Math.round(u)===Math.floor(u) ? u = Math.ceil(u) : u = Math.floor(u);
v = vR; w = wR;
break;
case 1:
Math.round(v)===Math.floor(v) ? v = Math.ceil(v) : v = Math.floor(v);
u = uR; w = wR;
break;
case 2:
Math.round(w)===Math.floor(w) ? w = Math.ceil(w) : w = Math.floor(w);
u = uR; v = vR;
break;
}
}
return {x: (3/2)*u, y: v-w};
}
Я еще раз взглянул на http://playtechs.blogspot.co.uk/2007/04/hex-grids.html и это математически очень аккуратно.
Однако подход Себастьяна, похоже, подходит к погоне и выполняет задачу в несколько строчек кода.
Прочитав раздел комментариев, вы обнаружите, что кто-то написал реализацию Python по адресу http://gist.github.com/583180
Я передам это здесь для потомков:
# copyright 2010 Eric Gradman
# free to use for any purpose, with or without attribution
# from an algorithm by James McNeill at
# http://playtechs.blogspot.com/2007/04/hex-grids.html
# the center of hex (0,0) is located at cartesian coordinates (0,0)
import numpy as np
# R ~ center of hex to edge
# S ~ edge length, also center to vertex
# T ~ "height of triangle"
real_R = 75. # in my application, a hex is 2*75 pixels wide
R = 2.
S = 2.*R/np.sqrt(3.)
T = S/2.
SCALE = real_R/R
# XM*X = I
# XM = Xinv
X = np.array([
[ 0, R],
[-S, S/2.]
])
XM = np.array([
[1./(2.*R), -1./S],
[1./R, 0. ]
])
# YM*Y = I
# YM = Yinv
Y = np.array([
[R, -R],
[S/2., S/2.]
])
YM = np.array([
[ 1./(2.*R), 1./S],
[-1./(2.*R), 1./S],
])
def cartesian2hex(cp):
"""convert cartesian point cp to hex coord hp"""
cp = np.multiply(cp, 1./SCALE)
Mi = np.floor(np.dot(XM, cp))
xi, yi = Mi
i = np.floor((xi+yi+2.)/3.)
Mj = np.floor(np.dot(YM, cp))
xj, yj = Mj
j = np.floor((xj+yj+2.)/3.)
hp = i,j
return hp
def hex2cartesian(hp):
"""convert hex center coordinate hp to cartesian centerpoint cp"""
i,j = hp
cp = np.array([
i*(2*R) + j*R,
j*(S+T)
])
cp = np.multiply(cp, SCALE)
return cp
Это дополнение к ответу Себастьяна Троя. Я бы оставил это как комментарий, но мне пока не хватает репутации.
Если вы хотите реализовать осевую систему координат, как описано здесь: http://www.redblobgames.com/grids/hexagons/
Вы можете внести небольшие изменения в код.
Вместо
// Is the row an odd number?
if (rowIsOdd)// Yes: Offset x to match the indent of the row
column = (int) ((x - halfWidth) / gridWidth);
else// No: Calculate normally
column = (int) (x / gridWidth);
использовать этот
float columnOffset = row * halfWidth;
column = (int)(x + columnOffset)/gridWidth; //switch + to - to align the grid the other way
Это приведет к тому, что координата (0, 2) будет находиться в том же диагональном столбце, что и (0, 0) и (0, 1), вместо того, чтобы находиться непосредственно под (0, 0).
Я не знаю, поможет ли это кому-нибудь, но я нашел гораздо более простое решение. Когда я создаю свой шестиугольник, я просто даю им среднюю точку и, находя ближайшую среднюю точку с помощью координат мыши, я могу найти, какая из них находится на!
Это похоже на другие ответы, но я думаю, что это более чистая реализация. Он в основном основан на руководстве Амита.
Обратите внимание, что северо-восточный угол дает ложный результат, подобный описанному P i.
Я использую кубические координаты. Часть секрета в том,
cube-round, который принимает результат с плавающей запятой и округляет его до ближайшего шестнадцатеричного числа.
Я считаю, что такие вещи легче достичь с матрицами. Сначала мы умножаем на матрицу перекоса и масштаба, что дает нам плавающие осевые шестнадцатеричные координаты, а затем округляем их в меньшую сторону, чтобы найти фактический гекс.
sizeсоответствует радиусу ячейки.
Вот это в паренскрипте:
(defmacro cube-round (coord)
;; round cube coordinates
`(let* ((x (@ ,coord 0))
(y (@ ,coord 1))
(z (@ ,coord 2))
;; rounded components - used in calculations
(rx (round x))
(ry (round y))
(rz (round z))
;; get the differential of each component
(diffx (abs (- rx x)))
(diffy (abs (- ry y)))
(diffz (abs (- rz z))))
;; at this point coordinates might not add up to 1 (which is required by cube coordinates). Find the component that changed the most, and reset it to -1 * (ra + rb).
(if (> diffx diffy diffz)
;; x was largest - reset it
(setf rx (* -1 (+ ry rz)))
(if (> diffy diffz)
;; y was largest
(setf ry (* -1 (+ rx rz)))
;; z was largest
(setf rz (* -1 (+ rx ry)))))
;; return final vector
(make-vec3 (list rx ry rz))))
(defmacro pixel-to-cube (coord size)
(let ((sqrt3 (sqrt 3.0)))
`(let* ((c ,coord)
;; skew+scale matrix for mapping pixel to axial coordinates [[sqrt(3)/3/size, -1/3/size], [0, 2/3/size]]
(m (make-mat2 (list
(/ (/ ,sqrt3 3.0) ,size) (/ (/ -1 3.0) ,size)
0 (/ (/ 2 3.0) ,size))))
(axial-coords (vec2-mat-mul m c))
(q (@ axial-coords 0))
(r (@ axial-coords 1))
;; make cube float coordinates from axial - make z = -1 * (x + y)
(cube-float (make-vec3-float
(list q r (* -1 (+ q r))))))
;; finally, round coordinates to snap to a cell
(cube-round cube-float))))
Я нашел другой способ узнать, находится ли мышь в шестиугольнике. Используя немного триггера, вы можете найти угол линии между мышью и центром шестиугольника, используя этот угол, вы можете определить, какова длина линии от центра шестиугольника до края шестиугольника при этом угол. Затем просто проверьте, что длина линии между мышью меньше ожидаемой длины до края шестиугольника. Если кому-то нужен пример кода, я могу поделиться.
Я знаю, что это очень поздно, но в настоящее время я работаю с шестиугольной сеткой и пытаюсь найти решение этой проблемы. Мне кажется, что сложные математические методы излишни, но я понимал, почему и как они работают. Почти случайно я нашел суперпростое решение, которое можно реализовать с помощью нескольких строк кода.
В моем примере у меня есть собственный класс Hexagon, содержащий переменную Point, которая хранит (x, y) центра шестиугольника. Затем я вычисляю и рисую шестиугольник на основе этого центрального значения.
Каждый класс Hexagon также присоединен к классу Tile, который хранит строку и переменную col (заданную при рисовании сетки).
Необходимые переменные: - Радиус - Ряд сетки - Столбик сетки - Центральная точка шестиугольника - Точка щелчка мышью (или другая заданная точка) - Список плиток / шестиугольников
Мой mouseListener:
addMouseListener(new MouseAdapter() {
@Override
public void mouseClicked(MouseEvent e) {
super.mouseClicked(e);
System.out.println("Mouse Click Registered");
double closestDistance = Double.MAX_VALUE;
int closestIndex = -1;
for (int i = 0; i < tiles.size(); i++) {
double distance = tiles.get(i).getDistance(new myPoint(e.getX(), e.getY()));
if (distance < closestDistance) {
closestDistance = distance;
if (closestDistance <= radius) {
closestIndex = i;
}
}
}
if (closestIndex > -1) {
Tile t = tiles.get(closestIndex);
System.out.println("Selected tile: " + t.getCol() + ", " + t.getRow());
}
}
});
Мой расчет выполнен из класса плитки:
public double getDistance(myPoint p) {
myPoint center = this.hexagon.getCenter();
double xd = center.x - p.x;
double yd = center.y - p.y;
return Math.abs(Math.sqrt((xd * xd) + (yd * yd)));
}
Что это значит. Просматривает список шестиугольников на карте, вычисляет абсолютное значение расстояния от указанной точки и центра шестиугольника. Если расстояние меньше, чем ранее рассчитанное расстояние, устанавливает это значение как наименьшее. Если это число меньше радиуса, устанавливает closestIndex для этого индекса #. Продолжается до конца петли плитки.
После цикла проверяет, что индекс значения был сохранен, если да, выбирает этот индекс.
ПРИМЕЧАНИЕ. Это, вероятно, можно было бы дополнительно оптимизировать, вычислив строку / столбец из указанной точки. Обладая этой информацией, вы можете ограничить количество просматриваемых плиток до плиток, звучащих в этой точке.
