Как найти кривую, которая проходит через сложные точки?

Question

У меня есть списки комплексных точек: орбита комплексной точки z под квадратичной функцией

 f(z) = z*z

Я знаю, что списки:

• z, z ^ 2, z ^ 4, z ^ 8,...
• (r, t), (r ^ 2, 2 * t),..., (r ^ (2 ^ n), t * 2 ^ n)

где:

• r = abs (z)
• t = arg (z)

Поэтому я думаю, что эти кривые будут экспоненциальными спиралями.

Но мой код:

 GiveParametric(radius,tMin,tMax) := 
 parametric(radius^t*cos(t),radius^t*sin(t),t,tMin,tMax)$

 GivePolar(radius, tMin,tMax) :=  polar(radius^(2^t),t,tMin,tMax)$

не работает.

Вот изображение 3 орбит (списков). Каждый список должен иметь свою собственную кривую (функцию)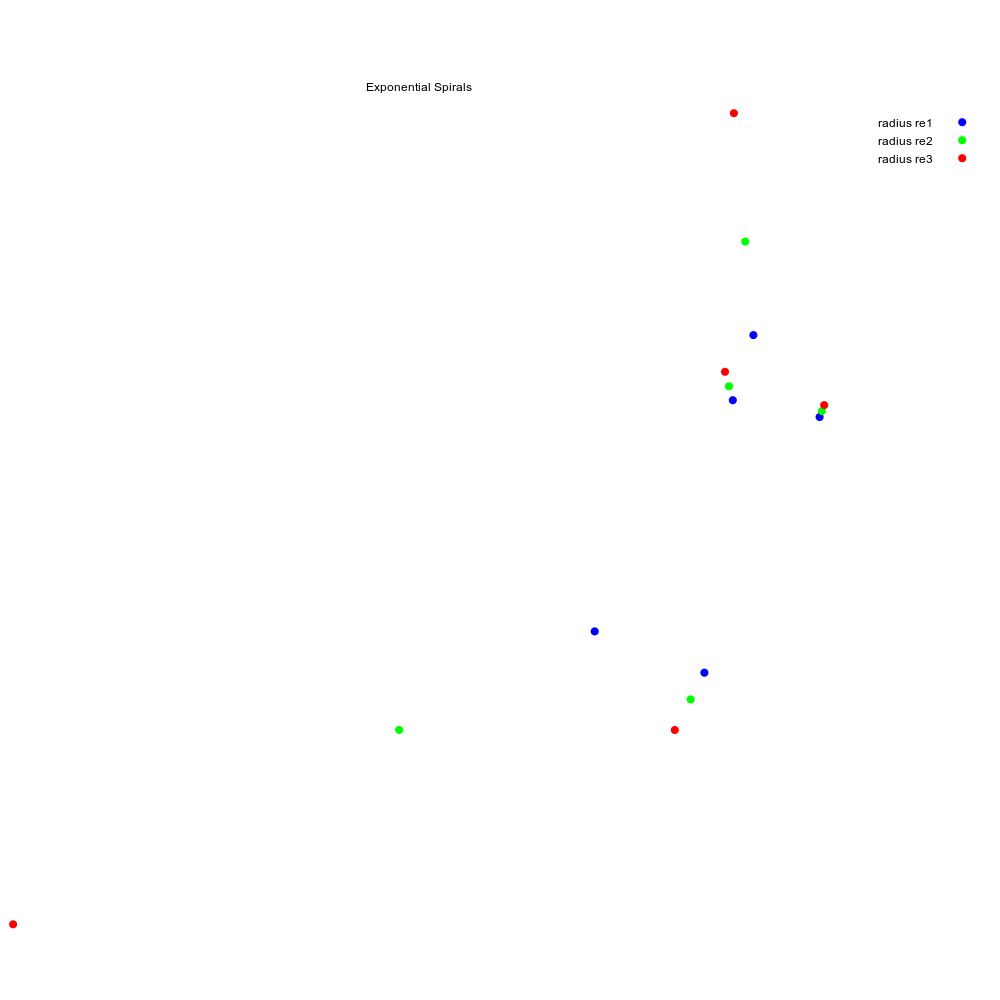

Вопрос:

Как нарисовать (или найти уравнения) кривых, которые проходят через эти точки?

Answer 1

Я использовал определение, чтобы нарисовать последовательность точек, соединенных линиями

GiveContOrbit(r0,a0,tMin, tMax, dt ):=
 block(
   [Orbit,a,r,t, b],
   t : tMin,
   b: 2^t,
   a:a0*b,
   r: r0^b,
   z: GiveZ(r,a),
   Orbit:[[realpart(z),imagpart(z)]], 
   for t:tMin thru tMax step dt do
    ( 
        b: 2^t,
    a:a0*b,
    r: r0^b,
    z: GiveZ(r,a), 
    Orbit:endcons([realpart(z),imagpart(z)],Orbit)),
    return(Orbit) 
    )$

Это не то, что я хотел, но кажется хорошим приближением. Как я вижу, кривые пересекаются.