Максимальный пул против нуля: потеря пространственной информации
Когда дело доходит до сверточных нейронных сетей, обычно есть много статей, рекомендующих различные стратегии. Я слышал, что люди говорят, что абсолютно необходимо добавить отступы к изображениям до свертки, иначе большая часть пространственной информации будет потеряна. С другой стороны, они рады использовать объединение, обычно максимальное объединение, для уменьшения размера изображений. Я предполагаю, что мысль здесь заключается в том, что максимальное объединение уменьшает пространственную информацию, но также уменьшает чувствительность к относительным позициям, так что это компромисс?
Я слышал, как другие люди говорили, что заполнение нулями не хранит больше информации, просто больше пустых данных. Это связано с тем, что, добавляя нули, вы не получите никакой реакции от вашего ядра, если часть информации отсутствует.
Я могу себе представить, что заполнение нулями работает, если у вас есть большие ядра с "значениями лома" по краям и источником активации, центрированным в меньшей области ядра?
Я был бы рад прочитать некоторые статьи о влиянии понижающей дискретизации с использованием пула и не использования отступов, но я не могу найти много об этом. Любые хорошие рекомендации или мысли? 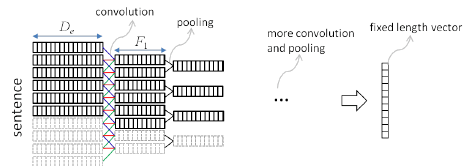
Рисунок: Пространственное понижение дискретизации с использованием свертки с обратным пулом (Researchgate)
2 ответа
Добавление отступов НЕ является "абсолютной необходимостью". Иногда может быть полезно контролировать размер вывода, чтобы он не уменьшался в результате свертки (он также может увеличивать вывод в зависимости от его размера и размера ядра). Единственная информация, которую добавляет нулевое заполнение, это состояние границы (или почти границы) объектов-пикселей в пределах входных данных, также зависящих от размера ядра. (Вы можете думать об этом как о паспарту в рамке рисунка)
Объединение имеет гораздо больше значения в сети. Объединение - это не "понижающая дискретизация" или "потеря пространственной информации". Сначала рассмотрим, что вычисления ядра были сделаны до объединения с полной пространственной информацией. Объединение в пул уменьшает размерность, но, к счастью, сохраняет информацию, полученную ядром ранее. И, таким образом, достигает одной из самых интересных вещей о Connet; устойчивость к смещению, повороту или искажению входа. Инвариантность, если она изучена, обнаруживается, даже если она появляется в другом месте или имеет искажения. Это также подразумевает обучение в возрастающем масштабе, обнаружение - опять же, надеюсь - иерархических структур в разных масштабах. И, конечно же, и это необходимо в коннетах, объединение в пул делает возможным вычисление по мере роста количества слоев.
Я тоже некоторое время занимался этим вопросом, и я также видел, что некоторые газеты упоминают эту же проблему. Вот недавняя статья, которую я нашел; Рекомбинаторные сети: изучение грубого до точного объединения функций. Я не полностью прочитал газету, но она, кажется, беспокоит ваш вопрос. Я могу обновить этот ответ, как только я полностью пойму бумагу.