Оптимизация для быстрого умножения, но медленного сложения: FMA и doubledouble
Когда я впервые получил процессор Haswell, я попытался реализовать FMA, чтобы определить множество Мандельброта. Основной алгоритм таков:
intn = 0;
for(int32_t i=0; i<maxiter; i++) {
floatn x2 = square(x), y2 = square(y); //square(x) = x*x
floatn r2 = x2 + y2;
booln mask = r2<cut; //booln is in the float domain non integer domain
if(!horizontal_or(mask)) break; //_mm256_testz_pd(mask)
n -= mask
floatn t = x*y; mul2(t); //mul2(t): t*=2
x = x2 - y2 + cx;
y = t + cy;
}
Это определяет, если n пиксели находятся в наборе Мандельброта. Так что для двойной плавающей запятой она работает более 4 пикселей (floatn = __m256d, intn = __m256i). Для этого требуется 4 умножения с плавающей запятой SIMD и четыре сложения с плавающей запятой SIMD.
Затем я изменил это для работы с FMA, как это
intn n = 0;
for(int32_t i=0; i<maxiter; i++) {
floatn r2 = mul_add(x,x,y*y);
booln mask = r2<cut;
if(!horizontal_or(mask)) break;
add_mask(n,mask);
floatn t = x*y;
x = mul_sub(x,x, mul_sub(y,y,cx));
y = mul_add(2.0f,t,cy);
}
где mul_add вызывает _mm256_fmad_pd и mul_sub вызывает _mm256_fmsub_pd, Этот метод использует 4 операции SIMD FMA и два умножения SIMD, что на две менее арифметические операции, чем без FMA. Кроме того, FMA и умножение могут использовать два порта и сложение только один.
Чтобы сделать мои тесты менее предвзятыми, я увеличил область, полностью находящуюся в наборе Мандельброта, поэтому все значения maxiter, В этом случае метод с использованием FMA происходит примерно на 27% быстрее. Это, безусловно, улучшение, но переход с SSE на AVX удвоил мою производительность, так что я надеялся на еще один фактор в два с FMA.
Но потом я нашел этот ответ в отношении FMA, где он говорит
Важным аспектом инструкции fused-multiply-add является (практически) бесконечная точность промежуточного результата. Это помогает с производительностью, но не так сильно, потому что две операции закодированы в одной инструкции. Это помогает с производительностью, потому что практически бесконечная точность промежуточного результата иногда важна, и очень дорого восстанавливать при обычном умножении и сложении, когда этот уровень Точность - это то, что нужно программисту.
и позже приводит пример двойного * двойного к двойному двойному умножению
high = a * b; /* double-precision approximation of the real product */
low = fma(a, b, -high); /* remainder of the real product */
Исходя из этого, я пришел к выводу, что я внедряю FMA неоптимально, и поэтому я решил внедрить SIMD double-double. Я реализовал двойное-двойное на основе бумаги Числа с плавающей точкой с расширенной точностью для вычислений на GPU. Бумага для двойного плавающего, поэтому я изменил его для двойного двойного. Кроме того, вместо упаковки одного значения типа double-double в регистры SIMD я упаковываю 4 значения типа double-double в один старший регистр AVX и один низкий регистр AVX.
Для набора Мандельброта мне действительно нужны двойное умножение и сложение. В этой статье это df64_add а также df64_mult функции. Изображение ниже показывает сборку для моего df64_mult функция для программного FMA (слева) и аппаратного FMA (справа). Это ясно показывает, что аппаратная FMA является большим улучшением для двойного двойного умножения.
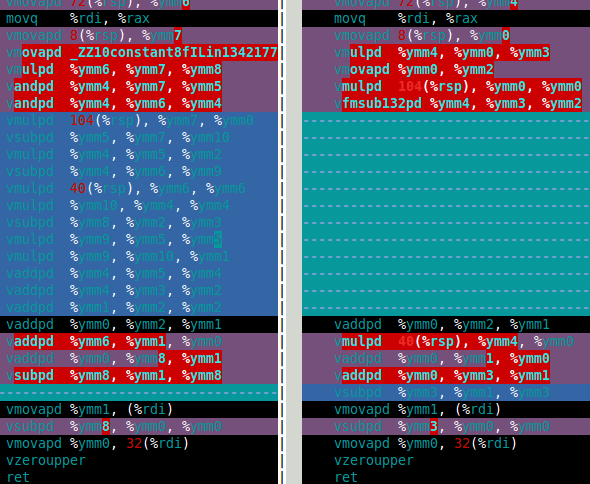
Так как же аппаратная FMA работает в расчете двойного-двойного Мандельброта? Ответ только на 15% быстрее, чем с программным обеспечением FMA. Это гораздо меньше, чем я надеялся. Для вычисления двойного двойного Мандельброта требуется 4 сложения двойного двойного и четыре умножения двойного двойного (x*x, y*y, x*y, а также 2*(x*y)). Тем не менее 2*(x*y) умножение тривиально для двойного-двойного, поэтому это умножение можно игнорировать в стоимости. Поэтому причина, по которой я думаю, что улучшение с использованием аппаратного FMA настолько мало, заключается в том, что в вычислениях преобладает медленное сложение двойного двойного (см. Сборку ниже).
Раньше умножение было медленнее, чем сложение (и программисты использовали несколько приемов, чтобы избежать умножения), но с Haswell кажется, что все наоборот. Не только из-за FMA, но и потому, что для умножения можно использовать два порта, но сложение - только один.
Итак, мои вопросы (наконец-то):
- Как оптимизировать, когда сложение медленное по сравнению с умножением?
- Есть ли алгебраический способ изменить мой алгоритм, чтобы использовать больше умножений и меньше сложений? Я знаю, что есть способ сделать обратное, например,
(x+y)*(x+y) - (x*x+y*y) = 2*x*yкоторые используют еще два дополнения для одного умножения меньше. - Есть ли способ просто использовать функцию df64_add (например, используя FMA)?
В случае, если кому-то интересно, метод double-double будет примерно в десять раз медленнее, чем double. Это не так уж и плохо, я думаю, что если бы был аппаратный тип с четверной точностью, он, вероятно, был бы как минимум вдвое медленнее, чем двойной, поэтому мой программный метод примерно в пять раз медленнее, чем я ожидал бы для аппаратного обеспечения, если бы он существовал.
df64_add сборка
vmovapd 8(%rsp), %ymm0
movq %rdi, %rax
vmovapd 72(%rsp), %ymm1
vmovapd 40(%rsp), %ymm3
vaddpd %ymm1, %ymm0, %ymm4
vmovapd 104(%rsp), %ymm5
vsubpd %ymm0, %ymm4, %ymm2
vsubpd %ymm2, %ymm1, %ymm1
vsubpd %ymm2, %ymm4, %ymm2
vsubpd %ymm2, %ymm0, %ymm0
vaddpd %ymm1, %ymm0, %ymm2
vaddpd %ymm5, %ymm3, %ymm1
vsubpd %ymm3, %ymm1, %ymm6
vsubpd %ymm6, %ymm5, %ymm5
vsubpd %ymm6, %ymm1, %ymm6
vaddpd %ymm1, %ymm2, %ymm1
vsubpd %ymm6, %ymm3, %ymm3
vaddpd %ymm1, %ymm4, %ymm2
vaddpd %ymm5, %ymm3, %ymm3
vsubpd %ymm4, %ymm2, %ymm4
vsubpd %ymm4, %ymm1, %ymm1
vaddpd %ymm3, %ymm1, %ymm0
vaddpd %ymm0, %ymm2, %ymm1
vsubpd %ymm2, %ymm1, %ymm2
vmovapd %ymm1, (%rdi)
vsubpd %ymm2, %ymm0, %ymm0
vmovapd %ymm0, 32(%rdi)
vzeroupper
ret
3 ответа
Чтобы ответить на мой третий вопрос, я нашел более быстрое решение для двойного сложения. Я нашел альтернативное определение в статье Реализация операторов с плавающей точкой на графическом оборудовании.
Theorem 5 (Add22 theorem) Let be ah+al and bh+bl the float-float arguments of the following
algorithm:
Add22 (ah ,al ,bh ,bl)
1 r = ah ⊕ bh
2 if | ah | ≥ | bh | then
3 s = ((( ah ⊖ r ) ⊕ bh ) ⊕ b l ) ⊕ a l
4 e l s e
5 s = ((( bh ⊖ r ) ⊕ ah ) ⊕ a l ) ⊕ b l
6 ( rh , r l ) = add12 ( r , s )
7 return (rh , r l)
Вот как я реализовал это (псевдокод):
static inline doubledoublen add22(doubledoublen const &a, doubledouble const &b) {
doublen aa,ab,ah,bh,al,bl;
booln mask;
aa = abs(a.hi); //_mm256_and_pd
ab = abs(b.hi);
mask = aa >= ab; //_mm256_cmple_pd
// z = select(cut,x,y) is a SIMD version of z = cut ? x : y;
ah = select(mask,a.hi,b.hi); //_mm256_blendv_pd
bh = select(mask,b.hi,a.hi);
al = select(mask,a.lo,b.lo);
bl = select(mask,b.lo,a.lo);
doublen r, s;
r = ah + bh;
s = (((ah - r) + bh) + bl ) + al;
return two_sum(r,s);
}
Это определение Add22 использует 11 дополнений вместо 20, но требует некоторого дополнительного кода, чтобы определить, |ah| >= |bh|, Здесь обсуждается, как реализовать SIMM-функции minmag и maxmag. К счастью, большая часть дополнительного кода не использует порт 1. Теперь только 12 команд идут на порт 1 вместо 20.
Вот форма анализа пропускной способности IACA для нового Add22
Throughput Analysis Report
--------------------------
Block Throughput: 12.05 Cycles Throughput Bottleneck: Port1
Port Binding In Cycles Per Iteration:
---------------------------------------------------------------------------------------
| Port | 0 - DV | 1 | 2 - D | 3 - D | 4 | 5 | 6 | 7 |
---------------------------------------------------------------------------------------
| Cycles | 0.0 0.0 | 12.0 | 2.5 2.5 | 2.5 2.5 | 2.0 | 10.0 | 0.0 | 2.0 |
---------------------------------------------------------------------------------------
| Num Of | Ports pressure in cycles | |
| Uops | 0 - DV | 1 | 2 - D | 3 - D | 4 | 5 | 6 | 7 | |
---------------------------------------------------------------------------------
| 1 | | | 0.5 0.5 | 0.5 0.5 | | | | | | vmovapd ymm3, ymmword ptr [rip]
| 1 | | | 0.5 0.5 | 0.5 0.5 | | | | | | vmovapd ymm0, ymmword ptr [rdx]
| 1 | | | 0.5 0.5 | 0.5 0.5 | | | | | | vmovapd ymm4, ymmword ptr [rsi]
| 1 | | | | | | 1.0 | | | | vandpd ymm2, ymm4, ymm3
| 1 | | | | | | 1.0 | | | | vandpd ymm3, ymm0, ymm3
| 1 | | 1.0 | | | | | | | CP | vcmppd ymm2, ymm3, ymm2, 0x2
| 1 | | | 0.5 0.5 | 0.5 0.5 | | | | | | vmovapd ymm3, ymmword ptr [rsi+0x20]
| 2 | | | | | | 2.0 | | | | vblendvpd ymm1, ymm0, ymm4, ymm2
| 2 | | | | | | 2.0 | | | | vblendvpd ymm4, ymm4, ymm0, ymm2
| 1 | | | 0.5 0.5 | 0.5 0.5 | | | | | | vmovapd ymm0, ymmword ptr [rdx+0x20]
| 2 | | | | | | 2.0 | | | | vblendvpd ymm5, ymm0, ymm3, ymm2
| 2 | | | | | | 2.0 | | | | vblendvpd ymm0, ymm3, ymm0, ymm2
| 1 | | 1.0 | | | | | | | CP | vaddpd ymm3, ymm1, ymm4
| 1 | | 1.0 | | | | | | | CP | vsubpd ymm2, ymm1, ymm3
| 1 | | 1.0 | | | | | | | CP | vaddpd ymm1, ymm2, ymm4
| 1 | | 1.0 | | | | | | | CP | vaddpd ymm1, ymm1, ymm0
| 1 | | 1.0 | | | | | | | CP | vaddpd ymm0, ymm1, ymm5
| 1 | | 1.0 | | | | | | | CP | vaddpd ymm2, ymm3, ymm0
| 1 | | 1.0 | | | | | | | CP | vsubpd ymm1, ymm2, ymm3
| 2^ | | | | | 1.0 | | | 1.0 | | vmovapd ymmword ptr [rdi], ymm2
| 1 | | 1.0 | | | | | | | CP | vsubpd ymm0, ymm0, ymm1
| 1 | | 1.0 | | | | | | | CP | vsubpd ymm1, ymm2, ymm1
| 1 | | 1.0 | | | | | | | CP | vsubpd ymm3, ymm3, ymm1
| 1 | | 1.0 | | | | | | | CP | vaddpd ymm0, ymm3, ymm0
| 2^ | | | | | 1.0 | | | 1.0 | | vmovapd ymmword ptr [rdi+0x20], ymm0
и вот анализ пропускной способности от старого
Throughput Analysis Report
--------------------------
Block Throughput: 20.00 Cycles Throughput Bottleneck: Port1
Port Binding In Cycles Per Iteration:
---------------------------------------------------------------------------------------
| Port | 0 - DV | 1 | 2 - D | 3 - D | 4 | 5 | 6 | 7 |
---------------------------------------------------------------------------------------
| Cycles | 0.0 0.0 | 20.0 | 2.0 2.0 | 2.0 2.0 | 2.0 | 0.0 | 0.0 | 2.0 |
---------------------------------------------------------------------------------------
| Num Of | Ports pressure in cycles | |
| Uops | 0 - DV | 1 | 2 - D | 3 - D | 4 | 5 | 6 | 7 | |
---------------------------------------------------------------------------------
| 1 | | | 1.0 1.0 | | | | | | | vmovapd ymm0, ymmword ptr [rsi]
| 1 | | | | 1.0 1.0 | | | | | | vmovapd ymm1, ymmword ptr [rdx]
| 1 | | | 1.0 1.0 | | | | | | | vmovapd ymm3, ymmword ptr [rsi+0x20]
| 1 | | 1.0 | | | | | | | CP | vaddpd ymm4, ymm0, ymm1
| 1 | | | | 1.0 1.0 | | | | | | vmovapd ymm5, ymmword ptr [rdx+0x20]
| 1 | | 1.0 | | | | | | | CP | vsubpd ymm2, ymm4, ymm0
| 1 | | 1.0 | | | | | | | CP | vsubpd ymm1, ymm1, ymm2
| 1 | | 1.0 | | | | | | | CP | vsubpd ymm2, ymm4, ymm2
| 1 | | 1.0 | | | | | | | CP | vsubpd ymm0, ymm0, ymm2
| 1 | | 1.0 | | | | | | | CP | vaddpd ymm2, ymm0, ymm1
| 1 | | 1.0 | | | | | | | CP | vaddpd ymm1, ymm3, ymm5
| 1 | | 1.0 | | | | | | | CP | vsubpd ymm6, ymm1, ymm3
| 1 | | 1.0 | | | | | | | CP | vsubpd ymm5, ymm5, ymm6
| 1 | | 1.0 | | | | | | | CP | vsubpd ymm6, ymm1, ymm6
| 1 | | 1.0 | | | | | | | CP | vaddpd ymm1, ymm2, ymm1
| 1 | | 1.0 | | | | | | | CP | vsubpd ymm3, ymm3, ymm6
| 1 | | 1.0 | | | | | | | CP | vaddpd ymm2, ymm4, ymm1
| 1 | | 1.0 | | | | | | | CP | vaddpd ymm3, ymm3, ymm5
| 1 | | 1.0 | | | | | | | CP | vsubpd ymm4, ymm2, ymm4
| 1 | | 1.0 | | | | | | | CP | vsubpd ymm1, ymm1, ymm4
| 1 | | 1.0 | | | | | | | CP | vaddpd ymm0, ymm1, ymm3
| 1 | | 1.0 | | | | | | | CP | vaddpd ymm1, ymm2, ymm0
| 1 | | 1.0 | | | | | | | CP | vsubpd ymm2, ymm1, ymm2
| 2^ | | | | | 1.0 | | | 1.0 | | vmovapd ymmword ptr [rdi], ymm1
| 1 | | 1.0 | | | | | | | CP | vsubpd ymm0, ymm0, ymm2
| 2^ | | | | | 1.0 | | | 1.0 | | vmovapd ymmword ptr [rdi+0x20], ymm0
Лучшее решение было бы, если бы помимо FMA было три инструкции с одним операндом в режиме округления. Мне кажется, там должны быть одиночные инструкции режима округления для
a + b + c
a * b + c //FMA - this is the only one in x86 so far
a * b * c
Вы упоминаете следующий код:
vsubpd %ymm0, %ymm4, %ymm2
vsubpd %ymm2, %ymm1, %ymm1 <-- immediate dependency ymm2
vsubpd %ymm2, %ymm4, %ymm2
vsubpd %ymm2, %ymm0, %ymm0 <-- immediate dependency ymm2
vaddpd %ymm1, %ymm0, %ymm2 <-- immediate dependency ymm0
vaddpd %ymm5, %ymm3, %ymm1
vsubpd %ymm3, %ymm1, %ymm6 <-- immediate dependency ymm1
vsubpd %ymm6, %ymm5, %ymm5 <-- immediate dependency ymm6
vsubpd %ymm6, %ymm1, %ymm6 <-- dependency ymm1, ymm6
vaddpd %ymm1, %ymm2, %ymm1
vsubpd %ymm6, %ymm3, %ymm3 <-- dependency ymm6
vaddpd %ymm1, %ymm4, %ymm2
vaddpd %ymm5, %ymm3, %ymm3 <-- dependency ymm3
vsubpd %ymm4, %ymm2, %ymm4
vsubpd %ymm4, %ymm1, %ymm1 <-- immediate dependency ymm4
vaddpd %ymm3, %ymm1, %ymm0 <-- immediate dependency ymm1, ymm3
vaddpd %ymm0, %ymm2, %ymm1 <-- immediate dependency ymm0
vsubpd %ymm2, %ymm1, %ymm2 <-- immediate dependency ymm1
если вы тщательно проверяете, это в основном зависимые операции, и основное правило об эффективности задержки / пропускной способности не соблюдается. Большинство инструкций зависит от результата предыдущего или двух инструкций ранее. Эта последовательность содержит критический путь из 30 циклов (около 9 или 10 инструкций о "задержке 3 циклов"/"пропускной способности 1 цикла").
Ваша IACA сообщает инструкцию "CP" => в критическом пути, и оценочная стоимость составляет 20 циклов пропускной способности. Вы должны получить отчет о задержке, потому что именно он имеет значение, если вы заинтересованы в скорости выполнения.
Чтобы избавиться от стоимости этого критического пути, вы должны чередовать еще около 20 аналогичных инструкций, если компилятор не может этого сделать (например, потому что ваш код double-double находится в отдельной библиотеке, скомпилированной без оптимизации -flto и vzeroupper везде при входе и выходе из функции, vectorizer хорошо работает только с встроенным кодом).
Возможность состоит в том, чтобы запустить 2 вычисления параллельно (см. О сшивании кода в предыдущем посте, чтобы улучшить конвейерную обработку)
Если я предполагаю, что ваш двойной-двойной код выглядит как эта "стандартная" реализация
// (r,e) = x + y
#define two_sum(x, y, r, e)
do { double t; r = x + y; t = r - x; e = (x - (r - t)) + (y - t); } while (0)
#define two_difference(x, y, r, e) \
do { double t; r = x - y; t = r - x; e = (x - (r - t)) - (y + t); } while (0)
.....
Затем вы должны рассмотреть следующий код, где инструкции чередуются с довольно мелким зерном.
// (r1, e1) = x1 + y1, (r2, e2) x2 + y2
#define two_sum(x1, y1, x2, y2, r1, e1, r2, e2)
do { double t1, t2 \
r1 = x1 + y1; r2 = x2 + y2; \
t1 = r1 - x1; t2 = r2 - x2; \
e1 = (x1 - (r1 - t1)) + (y1 - t1); e2 = (x2 - (r2 - t2)) + (y2 - t2); \
} while (0)
....
Затем создается код, подобный следующему (примерно такой же критический путь в отчете о задержке и около 35 инструкций). Для получения подробной информации о времени выполнения, выполнение вне очереди должно выполняться без остановки.
vsubsd %xmm2, %xmm0, %xmm8
vsubsd %xmm3, %xmm1, %xmm1
vaddsd %xmm4, %xmm4, %xmm4
vaddsd %xmm5, %xmm5, %xmm5
vsubsd %xmm0, %xmm8, %xmm9
vsubsd %xmm9, %xmm8, %xmm10
vaddsd %xmm2, %xmm9, %xmm2
vsubsd %xmm10, %xmm0, %xmm0
vsubsd %xmm2, %xmm0, %xmm11
vaddsd %xmm14, %xmm4, %xmm2
vaddsd %xmm11, %xmm1, %xmm12
vsubsd %xmm4, %xmm2, %xmm0
vaddsd %xmm12, %xmm8, %xmm13
vsubsd %xmm0, %xmm2, %xmm11
vsubsd %xmm0, %xmm14, %xmm1
vaddsd %xmm6, %xmm13, %xmm3
vsubsd %xmm8, %xmm13, %xmm8
vsubsd %xmm11, %xmm4, %xmm4
vsubsd %xmm13, %xmm3, %xmm15
vsubsd %xmm8, %xmm12, %xmm12
vaddsd %xmm1, %xmm4, %xmm14
vsubsd %xmm15, %xmm3, %xmm9
vsubsd %xmm15, %xmm6, %xmm6
vaddsd %xmm7, %xmm12, %xmm7
vsubsd %xmm9, %xmm13, %xmm10
vaddsd 16(%rsp), %xmm5, %xmm9
vaddsd %xmm6, %xmm10, %xmm15
vaddsd %xmm14, %xmm9, %xmm10
vaddsd %xmm15, %xmm7, %xmm13
vaddsd %xmm10, %xmm2, %xmm15
vaddsd %xmm13, %xmm3, %xmm6
vsubsd %xmm2, %xmm15, %xmm2
vsubsd %xmm3, %xmm6, %xmm3
vsubsd %xmm2, %xmm10, %xmm11
vsubsd %xmm3, %xmm13, %xmm0
Резюме:
встроить ваш двойной двойной исходный код: компилятор и векторизатор не могут оптимизировать вызовы функций из-за ограничений ABI и доступа к памяти из-за боязни совмещения имен.
Сшивать код, чтобы сбалансировать пропускную способность и задержку и максимизировать использование портов ЦП (а также максимизировать количество команд за цикл), пока компилятор не выливает слишком много регистров в память.
Вы можете отслеживать влияние оптимизации с помощью утилиты perf (пакеты linux-tools-generic и linux-cloud-tools-generic), чтобы получить количество выполненных инструкций и количество инструкций за цикл.
Чтобы ускорить алгоритм, я использую упрощенную версию, основанную на 2 FMA, 1 MUL и 2 Add. Я обрабатываю 8 итераций таким образом. Затем вычислите радиус выхода и откатите последние 8 итераций, если это необходимо.
Следующий критический цикл X = X^2 + C, написанный с использованием встроенных функций x86, прекрасно разворачивается компилятором, и после развертывания вы обнаружите, что две операции FMA не сильно зависят друг от друга.
// IACA_START;
for (j = 0; j < 8; j++) {
Xrm = _mm256_mul_ps(Xre, Xim);
Xtt = _mm256_fmsub_ps(Xim, Xim, Cre);
Xrm = _mm256_add_ps(Xrm, Xrm);
Xim = _mm256_add_ps(Cim, Xrm);
Xre = _mm256_fmsub_ps(Xre, Xre, Xtt);
} // for
// IACA_END;
А затем я вычисляю запасной радиус (|X| <порог), который стоит другую FMA и другое умножение, только каждые 8 итераций.
cmp = _mm256_mul_ps(Xre, Xre);
cmp = _mm256_fmadd_ps(Xim, Xim, cmp);
cmp = _mm256_cmp_ps(cmp, vec_threshold, _CMP_LE_OS);
if (_mm256_testc_si256((__m256i) cmp, vec_one)) {
i += 8;
continue;
}
Вы упоминаете, что "сложение происходит медленно", это не совсем так, но вы правы, пропускная способность умножения с течением времени возрастает на последних архитектурах.
Задержки умножения и зависимости являются ключевыми. FMA имеет пропускную способность 1 цикл и задержку 5 циклов. выполнение независимых инструкций FMA может перекрываться.
Дополнения, основанные на результате умножения, получают полную задержку.
Таким образом, вы должны сломать эти непосредственные зависимости, выполнив "сшивание кода" и вычислить 2 точки в одном цикле, и просто чередовать код перед проверкой с IACA, что будет происходить. Следующий код имеет 2 набора переменных (с суффиксом 0 и 1 для X0=X0^2+C0, X1=X1^2+C1) и начинает заполнять отверстия FMA
for (j = 0; j < 8; j++) {
Xrm0 = _mm256_mul_ps(Xre0, Xim0);
Xrm1 = _mm256_mul_ps(Xre1, Xim1);
Xtt0 = _mm256_fmsub_ps(Xim0, Xim0, Cre);
Xtt1 = _mm256_fmsub_ps(Xim1, Xim1, Cre);
Xrm0 = _mm256_add_ps(Xrm0, Xrm0);
Xrm1 = _mm256_add_ps(Xrm1, Xrm1);
Xim0 = _mm256_add_ps(Cim0, Xrm0);
Xim1 = _mm256_add_ps(Cim1, Xrm1);
Xre0 = _mm256_fmsub_ps(Xre0, Xre0, Xtt0);
Xre1 = _mm256_fmsub_ps(Xre1, Xre1, Xtt1);
} // for
Подвести итоги,
- Вы можете вдвое сократить количество инструкций в вашем критическом цикле
- Вы можете добавить больше независимых инструкций и получить преимущество высокой пропускной способности по сравнению с низкой задержкой умножения, а также умножением и сложением.