Создание PDF-файлов, рисование полигонов с закругленными углами
Какой инструмент подходит для работы, если я хочу написать скрипт на Python, который производит векторную графику в формате PDF? В частности, мне нужно нарисовать заполненные многоугольники со скругленными углами (т.е. плоские фигуры, которые состоят из прямых линий и дуг окружности).
Кажется, что matplotlib позволяет довольно легко рисовать прямоугольники со скругленными углами и обычные многоугольники с острыми углами. Однако, чтобы нарисовать многоугольники со скругленными углами, мне кажется, что сначала нужно вычислить кривую Безье, которая приближается к форме.
Есть ли что-нибудь более простое доступное? Или есть другая библиотека, которую я могу использовать для вычисления кривой Безье, которая приближается к форме, которую я хочу создать? В идеале я бы просто указывал пару (местоположение, угловой радиус) для каждой вершины.
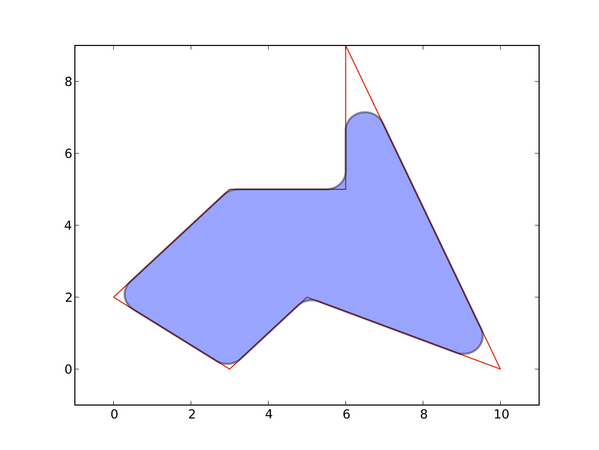
Вот пример: я хотел бы указать красный многоугольник (+ радиус каждого угла), и библиотека выведет серый рисунок:
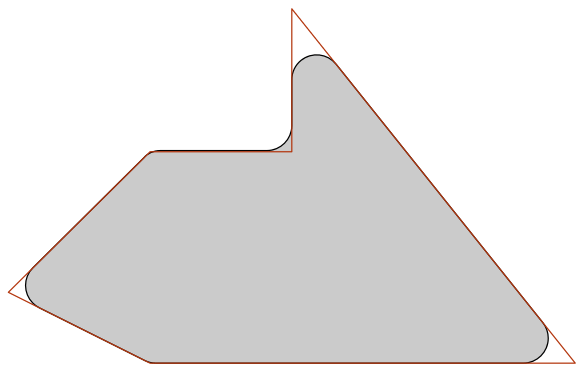
(Для выпуклых многоугольников я мог бы обмануть и использовать толстую ручку, чтобы нарисовать контур многоугольника. Однако это не работает в невыпуклом случае.)
2 ответа
Что касается создания файлов PDF, я бы посоветовал взглянуть на библиотеку cairo, библиотеку векторной графики, которая поддерживает "рисование" на поверхностях PDF. У него также есть привязки Python.
Что касается рисования полигонов с закругленными углами, я не знаю ни одной графической библиотеки, которая бы поддерживала это из коробки.
Но не должно быть слишком сложно вычислять координаты дуги в углах многоугольника с учетом радиуса угла. В основном вы должны найти точку на биссектрисе угла двух соседних ребер, которая имеет расстояние r (т.е. желаемый радиус) с обоих краев. Это центр дуги, для нахождения начальной и конечной точки вы будете проецироваться из этой точки на два ребра.
Могут быть нетривиальные случаи, например, что делать, если ребра многоугольника слишком короткие, чтобы соответствовать двум дугам (я думаю, вам придется выбирать меньший радиус в этом случае), и, возможно, другие, в настоящее время я не знаю из...
НТН
Вот несколько хакерское решение matplotlib. Основные осложнения связаны с использованием matplotlib Path объекты для построения композита Path,
#!/usr/bin/env python
import numpy as np
from matplotlib.path import Path
from matplotlib.patches import PathPatch, Polygon
from matplotlib.transforms import Bbox, BboxTransformTo
def side(a, b, c):
"On which side of line a-b is point c? Returns -1, 0, or 1."
return np.sign(np.linalg.det(np.c_[[a,b,c],[1,1,1]]))
def center((prev, curr, next), radius):
"Find center of arc approximating corner at curr."
p0, p1 = prev
c0, c1 = curr
n0, n1 = next
dp = radius * np.hypot(c1 - p1, c0 - p0)
dn = radius * np.hypot(c1 - n1, c0 - n0)
p = p1 * c0 - p0 * c1
n = n1 * c0 - n0 * c1
results = \
np.linalg.solve([[p1 - c1, c0 - p0],
[n1 - c1, c0 - n0]],
[[p - dp, p - dp, p + dp, p + dp],
[n - dn, n + dn, n - dn, n + dn]])
side_n = side(prev, curr, next)
side_p = side(next, curr, prev)
for r in results.T:
if (side(prev, curr, r), side(next, curr, r)) == (side_n, side_p):
return r
raise ValueError, "Cannot find solution"
def proj((prev, curr, next), center):
"Project center onto lines prev-curr and next-curr."
p0, p1 = prev = np.asarray(prev)
c0, c1 = curr = np.asarray(curr)
n0, n1 = next = np.asarray(next)
pc = curr - prev
nc = curr - next
pc2 = np.dot(pc, pc)
nc2 = np.dot(nc, nc)
return (prev + np.dot(center - prev, pc)/pc2 * pc,
next + np.dot(center - next, nc)/nc2 * nc)
def rad2deg(angle):
return angle * 180.0 / np.pi
def angle(center, point):
x, y = np.asarray(point) - np.asarray(center)
return np.arctan2(y, x)
def arc_path(center, start, end):
"Return a Path for an arc from start to end around center."
# matplotlib arcs always go ccw so we may need to mirror
mirror = side(center, start, end) < 0
if mirror:
start *= [1, -1]
center *= [1, -1]
end *= [1, -1]
return Path.arc(rad2deg(angle(center, start)),
rad2deg(angle(center, end))), \
mirror
def path(vertices, radii):
"Return a Path for a closed rounded polygon."
if np.isscalar(radii):
radii = np.repeat(radii, len(vertices))
else:
radii = np.asarray(radii)
pv = []
pc = []
first = True
for i in range(len(vertices)):
if i == 0:
seg = (vertices[-1], vertices[0], vertices[1])
elif i == len(vertices) - 1:
seg = (vertices[-2], vertices[-1], vertices[0])
else:
seg = vertices[i-1:i+2]
r = radii[i]
c = center(seg, r)
a, b = proj(seg, c)
arc, mirror = arc_path(c, a, b)
m = [1,1] if not mirror else [1,-1]
bb = Bbox([c, c + (r, r)])
iter = arc.iter_segments(BboxTransformTo(bb))
for v, c in iter:
if c == Path.CURVE4:
pv.extend([m * v[0:2], m * v[2:4], m * v[4:6]])
pc.extend([c, c, c])
elif c == Path.MOVETO:
pv.append(m * v)
if first:
pc.append(Path.MOVETO)
first = False
else:
pc.append(Path.LINETO)
pv.append([0,0])
pc.append(Path.CLOSEPOLY)
return Path(pv, pc)
if __name__ == '__main__':
from matplotlib import pyplot
fig = pyplot.figure()
ax = fig.add_subplot(111)
vertices = [[3,0], [5,2], [10,0], [6,9], [6,5], [3, 5], [0,2]]
patch = Polygon(vertices, edgecolor='red', facecolor='None',
linewidth=1)
ax.add_patch(patch)
patch = PathPatch(path(vertices, 0.5),
edgecolor='black', facecolor='blue', alpha=0.4,
linewidth=2)
ax.add_patch(patch)
ax.set_xlim(-1, 11)
ax.set_ylim(-1, 9)
fig.savefig('foo.pdf')