Получение стандартных ошибок для подогнанных параметров с использованием метода optimize.leastsq в python
У меня есть набор данных (смещение в зависимости от времени), которые я приспособил для пары уравнений с помощью метода optimize.leastsq. Я сейчас ищу, чтобы получить значения ошибок по подобранным параметрам. Просматривая документацию, выведенная матрица является матрицей Якоби, и я должен умножить ее на остаточную матрицу, чтобы получить мои значения. К сожалению, я не статистика, поэтому я немного тону в терминологии.
Из того, что я понимаю, все, что мне нужно, это ковариационная матрица, которая соответствует моим подогнанным параметрам, так что я могу получить квадратный корень из диагональных элементов, чтобы получить стандартную ошибку для подобранных параметров. Я смутно помню, что ковариационная матрица - это то, что выводится из метода optimize.leastsq. Это правильно? Если нет, то как бы вы получили остаточную матрицу для умножения выходного якобиана на мою ковариационную матрицу?
Любая помощь будет принята с благодарностью. Я очень плохо знаком с Python и поэтому прошу прощения, если вопрос окажется основным.
подходящий код выглядит следующим образом:
fitfunc = lambda p, t: p[0]+p[1]*np.log(t-p[2])+ p[3]*t # Target function'
errfunc = lambda p, t, y: (fitfunc(p, t) - y)# Distance to the target function
p0 = [ 1,1,1,1] # Initial guess for the parameters
out = optimize.leastsq(errfunc, p0[:], args=(t, disp,), full_output=1)
Аргументы t и disp - это массив значений времени и смещения (в основном только 2 столбца данных). Я импортировал все необходимое в топе кода. Установленные значения и матрица, представленные в выходных данных, следующие:
[ 7.53847074e-07 1.84931494e-08 3.25102795e+01 -3.28882437e-11]
[[ 3.29326356e-01 -7.43957919e-02 8.02246944e+07 2.64522183e-04]
[ -7.43957919e-02 1.70872763e-02 -1.76477289e+07 -6.35825520e-05]
[ 8.02246944e+07 -1.76477289e+07 2.51023348e+16 5.87705672e+04]
[ 2.64522183e-04 -6.35825520e-05 5.87705672e+04 2.70249488e-07]]
Я подозреваю, что в данный момент подгонка немного подозрительна. Это будет подтверждено, когда я смогу вывести ошибки.
3 ответа
Обновлено 6/6/2016
Получение правильных ошибок в параметрах соответствия в большинстве случаев может быть неуловимым.
Давайте подумаем о подборе функции y=f(x) для которого у вас есть набор точек данных (x_i, y_i, yerr_i), где i это индекс, который проходит по каждой из ваших точек данных.
В большинстве физических измерений ошибка yerr_i является систематической неопределенностью измерительного устройства или процедуры, и поэтому ее можно рассматривать как постоянную, которая не зависит от i,
Какую функцию подбора использовать и как получить ошибки параметров?
optimize.leastsq Метод вернет дробно-ковариационную матрицу. Умножение всех элементов этой матрицы на остаточную дисперсию (т.е. уменьшенный хи-квадрат) и получение квадратного корня из диагональных элементов даст вам оценку стандартного отклонения параметров подгонки. Я включил код для этого в одну из функций ниже.
С другой стороны, если вы используете optimize.curvefitпервая часть описанной выше процедуры (умножение на уменьшенный хи-квадрат) выполняется за кулисами. Затем вам нужно взять квадратный корень из диагональных элементов ковариационной матрицы, чтобы получить оценку стандартного отклонения параметров подгонки.
Более того, optimize.curvefit предоставляет необязательные параметры для более общих случаев, когда yerr_i значение отличается для каждой точки данных. Из документации:
sigma : None or M-length sequence, optional
If not None, the uncertainties in the ydata array. These are used as
weights in the least-squares problem
i.e. minimising ``np.sum( ((f(xdata, *popt) - ydata) / sigma)**2 )``
If None, the uncertainties are assumed to be 1.
absolute_sigma : bool, optional
If False, `sigma` denotes relative weights of the data points.
The returned covariance matrix `pcov` is based on *estimated*
errors in the data, and is not affected by the overall
magnitude of the values in `sigma`. Only the relative
magnitudes of the `sigma` values matter.
Как я могу быть уверен, что мои ошибки верны?
Определение правильной оценки стандартной ошибки в подобранных параметрах является сложной статистической задачей. Результаты ковариационной матрицы, как реализовано optimize.curvefit а также optimize.leastsq фактически полагаться на предположения, касающиеся распределения вероятностей ошибок и взаимодействия между параметрами; взаимодействия, которые могут существовать, в зависимости от вашей конкретной функции соответствия f(x),
На мой взгляд, лучший способ справиться со сложным f(x) использовать метод начальной загрузки, который описан в этой ссылке.
Давайте посмотрим несколько примеров
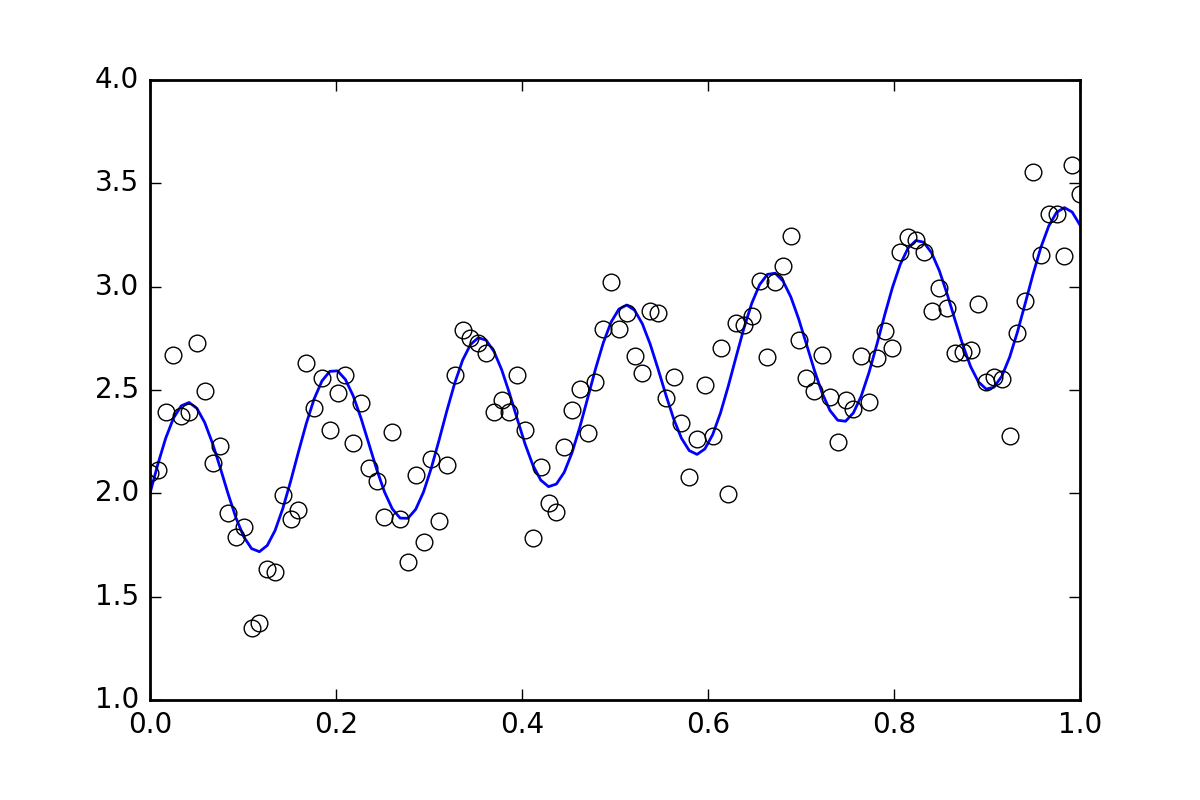
Сначала немного стандартного кода. Давайте определим функцию волнистой линии и сгенерируем некоторые данные со случайными ошибками. Мы сгенерируем набор данных с небольшой случайной ошибкой.
import numpy as np
from scipy import optimize
import random
def f( x, p0, p1, p2):
return p0*x + 0.4*np.sin(p1*x) + p2
def ff(x, p):
return f(x, *p)
# These are the true parameters
p0 = 1.0
p1 = 40
p2 = 2.0
# These are initial guesses for fits:
pstart = [
p0 + random.random(),
p1 + 5.*random.random(),
p2 + random.random()
]
%matplotlib inline
import matplotlib.pyplot as plt
xvals = np.linspace(0., 1, 120)
yvals = f(xvals, p0, p1, p2)
# Generate data with a bit of randomness
# (the noise-less function that underlies the data is shown as a blue line)
xdata = np.array(xvals)
np.random.seed(42)
err_stdev = 0.2
yvals_err = np.random.normal(0., err_stdev, len(xdata))
ydata = f(xdata, p0, p1, p2) + yvals_err
plt.plot(xvals, yvals)
plt.plot(xdata, ydata, 'o', mfc='None')
Теперь давайте подгоним функцию, используя различные доступные методы:
`optimize.leastsq`
def fit_leastsq(p0, datax, datay, function):
errfunc = lambda p, x, y: function(x,p) - y
pfit, pcov, infodict, errmsg, success = \
optimize.leastsq(errfunc, p0, args=(datax, datay), \
full_output=1, epsfcn=0.0001)
if (len(datay) > len(p0)) and pcov is not None:
s_sq = (errfunc(pfit, datax, datay)**2).sum()/(len(datay)-len(p0))
pcov = pcov * s_sq
else:
pcov = np.inf
error = []
for i in range(len(pfit)):
try:
error.append(np.absolute(pcov[i][i])**0.5)
except:
error.append( 0.00 )
pfit_leastsq = pfit
perr_leastsq = np.array(error)
return pfit_leastsq, perr_leastsq
pfit, perr = fit_leastsq(pstart, xdata, ydata, ff)
print("\n# Fit parameters and parameter errors from lestsq method :")
print("pfit = ", pfit)
print("perr = ", perr)
# Fit parameters and parameter errors from lestsq method :
pfit = [ 1.04951642 39.98832634 1.95947613]
perr = [ 0.0584024 0.10597135 0.03376631]
`optimize.curve_fit`
def fit_curvefit(p0, datax, datay, function, yerr=err_stdev, **kwargs):
"""
Note: As per the current documentation (Scipy V1.1.0), sigma (yerr) must be:
None or M-length sequence or MxM array, optional
Therefore, replace:
err_stdev = 0.2
With:
err_stdev = [0.2 for item in xdata]
Or similar, to create an M-length sequence for this example.
"""
pfit, pcov = \
optimize.curve_fit(f,datax,datay,p0=p0,\
sigma=yerr, epsfcn=0.0001, **kwargs)
error = []
for i in range(len(pfit)):
try:
error.append(np.absolute(pcov[i][i])**0.5)
except:
error.append( 0.00 )
pfit_curvefit = pfit
perr_curvefit = np.array(error)
return pfit_curvefit, perr_curvefit
pfit, perr = fit_curvefit(pstart, xdata, ydata, ff)
print("\n# Fit parameters and parameter errors from curve_fit method :")
print("pfit = ", pfit)
print("perr = ", perr)
# Fit parameters and parameter errors from curve_fit method :
pfit = [ 1.04951642 39.98832634 1.95947613]
perr = [ 0.0584024 0.10597135 0.03376631]
`bootstrap`
def fit_bootstrap(p0, datax, datay, function, yerr_systematic=0.0):
errfunc = lambda p, x, y: function(x,p) - y
# Fit first time
pfit, perr = optimize.leastsq(errfunc, p0, args=(datax, datay), full_output=0)
# Get the stdev of the residuals
residuals = errfunc(pfit, datax, datay)
sigma_res = np.std(residuals)
sigma_err_total = np.sqrt(sigma_res**2 + yerr_systematic**2)
# 100 random data sets are generated and fitted
ps = []
for i in range(100):
randomDelta = np.random.normal(0., sigma_err_total, len(datay))
randomdataY = datay + randomDelta
randomfit, randomcov = \
optimize.leastsq(errfunc, p0, args=(datax, randomdataY),\
full_output=0)
ps.append(randomfit)
ps = np.array(ps)
mean_pfit = np.mean(ps,0)
# You can choose the confidence interval that you want for your
# parameter estimates:
Nsigma = 1. # 1sigma gets approximately the same as methods above
# 1sigma corresponds to 68.3% confidence interval
# 2sigma corresponds to 95.44% confidence interval
err_pfit = Nsigma * np.std(ps,0)
pfit_bootstrap = mean_pfit
perr_bootstrap = err_pfit
return pfit_bootstrap, perr_bootstrap
pfit, perr = fit_bootstrap(pstart, xdata, ydata, ff)
print("\n# Fit parameters and parameter errors from bootstrap method :")
print("pfit = ", pfit)
print("perr = ", perr)
# Fit parameters and parameter errors from bootstrap method :
pfit = [ 1.05058465 39.96530055 1.96074046]
perr = [ 0.06462981 0.1118803 0.03544364]
наблюдения
Мы уже начинаем видеть что-то интересное, параметры и оценки ошибок для всех трех методов почти совпадают. Это хорошо!
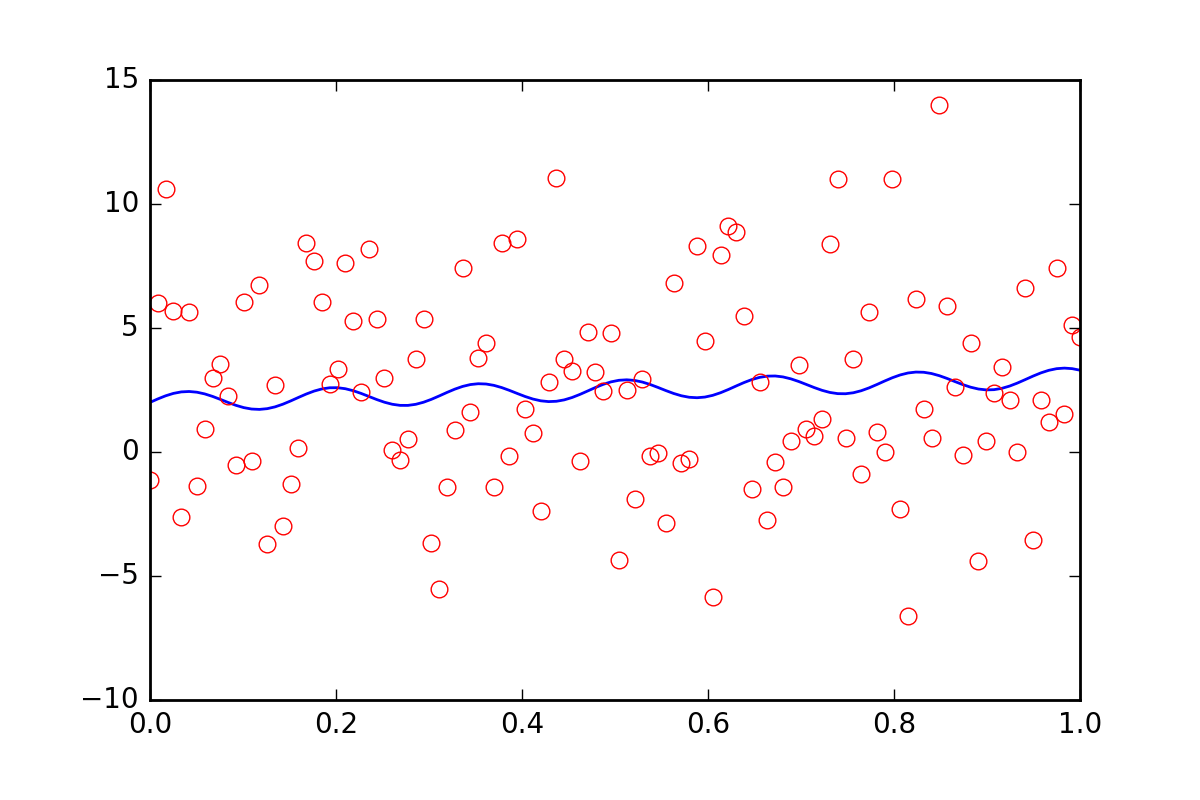
Теперь предположим, что мы хотим сообщить функциям подгонки, что в наших данных есть некоторая другая неопределенность, возможно, систематическая неопределенность, которая внесет дополнительную ошибку, в двадцать раз превышающую значение err_stdev, Это большая ошибка, на самом деле, если мы смоделируем некоторые данные с такой ошибкой, это будет выглядеть так:
Конечно, нет никакой надежды на то, что мы сможем восстановить параметры соответствия с этим уровнем шума.
Для начала давайте осознаем, что leastsq даже не позволяет нам вводить эту новую информацию систематической ошибки. Посмотрим что curve_fit делает, когда мы говорим об ошибке:
pfit, perr = fit_curvefit(pstart, xdata, ydata, ff, yerr=20*err_stdev)
print("\nFit parameters and parameter errors from curve_fit method (20x error) :")
print("pfit = ", pfit)
print("perr = ", perr)
Fit parameters and parameter errors from curve_fit method (20x error) :
pfit = [ 1.04951642 39.98832633 1.95947613]
perr = [ 0.0584024 0.10597135 0.03376631]
Whaat?? Это должно быть неправильно!
Это был конец истории, но недавно curve_fit добавил absolute_sigma необязательный параметр:
pfit, perr = fit_curvefit(pstart, xdata, ydata, ff, yerr=20*err_stdev, absolute_sigma=True)
print("\n# Fit parameters and parameter errors from curve_fit method (20x error, absolute_sigma) :")
print("pfit = ", pfit)
print("perr = ", perr)
# Fit parameters and parameter errors from curve_fit method (20x error, absolute_sigma) :
pfit = [ 1.04951642 39.98832633 1.95947613]
perr = [ 1.25570187 2.27847504 0.72600466]
Это немного лучше, но все же немного подозрительно. curve_fit считает, что мы можем получить сигнал от этого зашумленного сигнала с уровнем ошибки 10% в p1 параметр. Посмотрим что bootstrap должен сказать:
pfit, perr = fit_bootstrap(pstart, xdata, ydata, ff, yerr_systematic=20.0)
print("\nFit parameters and parameter errors from bootstrap method (20x error):")
print("pfit = ", pfit)
print("perr = ", perr)
Fit parameters and parameter errors from bootstrap method (20x error):
pfit = [ 2.54029171e-02 3.84313695e+01 2.55729825e+00]
perr = [ 6.41602813 13.22283345 3.6629705 ]
Ах, это, пожалуй, лучшая оценка ошибки в нашем параметре подгонки. bootstrap думает, что знает p1 с неопределенностью около 34%.
Резюме
optimize.leastsq а также optimize.curvefit предоставьте нам способ оценить ошибки в подгоночных параметрах, но мы не можем просто использовать эти методы, не ставя их под сомнение. bootstrap Это статистический метод, который использует грубую силу, и, по моему мнению, он имеет тенденцию работать лучше в ситуациях, которые может быть труднее интерпретировать.
Я настоятельно рекомендую посмотреть на конкретную проблему и попробовать curvefit а также bootstrap, Если они похожи, то curvefit гораздо дешевле вычислить, поэтому, вероятно, стоит использовать. Если они существенно отличаются, то мои деньги будут на bootstrap,
Нашел свой вопрос, пытаясь ответить на мой собственный похожий вопрос. Короткий ответ. cov_x что результаты наименьшего количества должны быть умножены на остаточную дисперсию. т.е.
s_sq = (func(popt, args)**2).sum()/(len(ydata)-len(p0))
pcov = pcov * s_sq
как в curve_fit.py, Это потому, что leastsq выводит дробно-ковариационную матрицу. Моя большая проблема заключалась в том, что остаточная дисперсия проявляется как что-то еще при поиске в Google.
Остаточная дисперсия - это просто уменьшенная площадь ци от вашей посадки.
Можно точно рассчитать погрешности в случае линейной регрессии. И действительно, функция leastsq выдает значения, которые отличаются:
import numpy as np
from scipy.optimize import leastsq
import matplotlib.pyplot as plt
A = 1.353
B = 2.145
yerr = 0.25
xs = np.linspace( 2, 8, 1448 )
ys = A * xs + B + np.random.normal( 0, yerr, len( xs ) )
def linearRegression( _xs, _ys ):
if _xs.shape[0] != _ys.shape[0]:
raise ValueError( 'xs and ys must be of the same length' )
xSum = ySum = xxSum = yySum = xySum = 0.0
numPts = 0
for i in range( len( _xs ) ):
xSum += _xs[i]
ySum += _ys[i]
xxSum += _xs[i] * _xs[i]
yySum += _ys[i] * _ys[i]
xySum += _xs[i] * _ys[i]
numPts += 1
k = ( xySum - xSum * ySum / numPts ) / ( xxSum - xSum * xSum / numPts )
b = ( ySum - k * xSum ) / numPts
sk = np.sqrt( ( ( yySum - ySum * ySum / numPts ) / ( xxSum - xSum * xSum / numPts ) - k**2 ) / numPts )
sb = np.sqrt( ( yySum - ySum * ySum / numPts ) - k**2 * ( xxSum - xSum * xSum / numPts ) ) / numPts
return [ k, b, sk, sb ]
def linearRegressionSP( _xs, _ys ):
defPars = [ 0, 0 ]
pars, pcov, infodict, errmsg, success = \
leastsq( lambda _pars, x, y: y - ( _pars[0] * x + _pars[1] ), defPars, args = ( _xs, _ys ), full_output=1 )
errs = []
if pcov is not None:
if( len( _xs ) > len(defPars) ) and pcov is not None:
s_sq = ( ( ys - ( pars[0] * _xs + pars[1] ) )**2 ).sum() / ( len( _xs ) - len( defPars ) )
pcov *= s_sq
for j in range( len( pcov ) ):
errs.append( pcov[j][j]**0.5 )
else:
errs = [ np.inf, np.inf ]
return np.append( pars, np.array( errs ) )
regr1 = linearRegression( xs, ys )
regr2 = linearRegressionSP( xs, ys )
print( regr1 )
print( 'Calculated sigma = %f' % ( regr1[3] * np.sqrt( xs.shape[0] ) ) )
print( regr2 )
#print( 'B = %f must be in ( %f,\t%f )' % ( B, regr1[1] - regr1[3], regr1[1] + regr1[3] ) )
plt.plot( xs, ys, 'bo' )
plt.plot( xs, regr1[0] * xs + regr1[1] )
plt.show()
выход:
[1.3481681543925064, 2.1729338701374137, 0.0036028493647274687, 0.0062446292528624348]
Calculated sigma = 0.237624 # quite close to yerr
[ 1.34816815 2.17293387 0.00360534 0.01907908]
Интересно, что дадут результаты Curvefit и Bootstrap...