Алгоритм трассировки границы в 2D массиве

Question

У меня есть двумерный массив целых чисел, которые представляют группировки (кристаллические зерна) на двумерной поверхности. что-то вроде этого: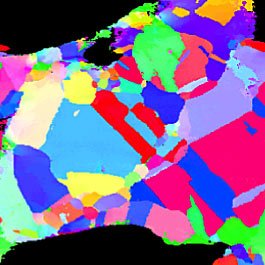(каждому пикселю этого изображения присваивается целое число в зависимости от группы, к которой оно принадлежит, поэтому каждому красному пикселю присваивается 1, например, каждому синему - 2)

учитывая координаты X,Y на границе между двумя такими группировками (пользователь щелкает там), как я могу отследить эту границу между этими двумя группировками, сохранив каждую пиксельную координату, которая находится вдоль границы, и получить две конечные координаты (я не касается случая вложения, где не было бы конечной точки, но петли)

какой бы алгоритм я ни придумал, он кажется утомительным для реализации, и я просто не могу представить, что никто не делал этого раньше. Любая помощь? Предпочтительно было бы решение в C#, но любая подсказка об алгоритме очень ценится.

РЕДАКТИРОВАТЬ:

Я должен был заявить, что собираюсь реализовать алгоритм для векторизации этой строки следующим образом:

1. между двумя конечными точками определяют линию
2. получить точку границы дальше от текущей линии, если она дальше, чем d, разделить линию в этой точке, так что есть два отрезка линии
3. повторять до тех пор, пока ни одна граничная точка не окажется дальше, чем d от линейной полосы

Я думал, что это было достаточно легко реализовать, поэтому я не утверждал это. Чтобы попасть туда, мне просто нужно было решить текущую проблему...

По вопросам:

как форматируются необработанные данные? - это просто short[,] labeling; с размером примерно 250x150 примерно так:

11111112222
11111222222
11112222222
11112222222 <- user clicks on leftmost 2 or rightmost 1 -> I want to trace that border
11111122222                                                down to the first
11111133322                                                encountered 3 and up to the
11333333333                                                frame-border

что такое конечная точка? - поскольку я думал о глобальных решениях, я мог бы описать конечную точку как: область 2x2, где 4 пикселя состоят из color1, color2 и, по крайней мере, одной трети разных цветов.

что смежно связано? - это не имеет значения для остальной части алгоритма, см. ниже

как насчет у-образных регионов? - Меня это не касается, вы можете предположить, что область color1 за границей имеет ширину не менее 2 пикселей, поэтому не имеет значения, говорим ли мы о 4 или 8 окрестностях.

что у меня сейчас есть? - сначала я попробовал алгоритм "ходьбы", что-то вроде mvds, но обнаружил, что я делаю шаг, соседский расчет и проверку во всех четырех направлениях, что было утомительно и выглядело ужасно. Я не нашел хорошего представления для "это направление, в котором был сделан последний шаг, не проверяйте этот пиксель на соседство".

Затем я отказался от алгоритма ходьбы и попробовал глобальный подход (например, фильтр): для каждого пикселя проверяйте, имеет ли он color1 AND цвет2 в своей 4-окрестности. С этим я получаю все границы между color1 и color2. Я собирался удалить все границы, которые не связаны с пользовательской координатой, вызванной нажатием кнопки, каким-то образом, но у меня возникла проблема: где находятся конечные точки?

Я все еще благодарен за дополнительный вклад. Сейчас я посмотрю, как далеко я могу пойти с алгоритмом mvds.

Answer 1

Я предполагаю, что вы уже определили 2 рассматриваемых цвета, например, как описано как mvds, в качестве шага предварительной обработки.

Я думаю, что вам будет полезно использовать систему координат, где каждый (x,y) представляет не пиксель, а точку, где касаются 4 пикселя. Затем вы можете написать функцию, чтобы определить, является ли север границей пиксельной границы, аналогично для юга, востока, запада (или, может быть, вы предпочитаете терминологию вверх / вниз / влево / вправо).

Начните с точки на границе, например, отсканируйте окрестность 4x4 для точки, которая имеет одну из N/S/E/W в качестве границы. Следуйте по этой границе до следующей точки, а затем отсканируйте все 4 направления, кроме направления, в котором вы пришли, для границы следующего пикселя. Повторяйте, пока не исчерпаете границы пикселей. Тогда вы знаете, что вы в одной конечной точке.

Вернитесь к началу и проведите границу в направлении, отличном от того, что вы изначально выбрали, пока не дойдете до другой конечной точки.

Это дает вам все границы пикселей. Каждая граница пикселя имеет цвет 1 на одной стороне и цвет 2 на другой стороне.

(Я бы подумал, что векторизация будет намного сложнее, чем определение границы, но вопрос не в этом, в основном, в вашем вопросе, верно? Для этого я бы начал с конечной точки и следовал бы последовательности границ пикселей border by border, в каждой точке проверяется, соответствует ли прямая линия от конечной точки до текущей точки границам пикселей. Как только это не произойдет, это конец одной линии, и вы начинаете новую линию.)

Answer 2

Ваше описание мне не совсем понятно, но если я вас правильно понимаю, вы хотите вычислить следующее:

• множество смежных точек цвета A, смежных с точкой цвета B
• который содержит данную отправную точку.

Учитывая эту спецификацию, ваш код практически пишет сам. Единственное, что вам нужно решить сейчас, это то, что означает "смежное соединение" (например, пиксели смежны только по их углам или нет?).

Также ваше описание неоднозначно. Рассмотрим y-образную область, где плечи области имеют ширину в один пиксель: это будет иметь три "конечных точки", если вы определите конечную точку как "член набора с одним соседом также в наборе". Если вы ослабите свое требование разрешить любое количество конечных точек, тогда ваш код может собирать набор конечных точек по мере необходимости.

РЕДАКТИРОВАТЬ

Рад, что ты решил свою проблему. Я набросал решение, которое дает это для вашей типовой задачи:

1111***2222
111**222222
111*2222222
111*2222222
111***22222
11111*33322
11333333333

Вот код, предоставленный только потому, что мне нужна проверка для его кодирования:-) Он написан для ясности, а не для скорости.

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Drawing;

namespace StackruEdgeDetection
{
    class Program
    {
        private static HashSet<Point> FindBorder(char[,] grid, Point start, char inside, char outside)
        {
            var border = new HashSet<Point> {};
            var endpoints = new HashSet<Point> { start };

            while (endpoints.Count != 0)
            {
                var p = endpoints.First();
                endpoints.Remove(p);
                border.Add(p);
                var newEndpoints = Neighbours(p).Where(q =>
                        Grid(grid, q) == inside &&
                        !border.Contains(q) &&
                        Neighbours(q).Any(r => Grid(grid, r) == outside)
                    );
                endpoints.UnionWith(newEndpoints);
            }

            return border;
        }

        private static IEnumerable<Point> Neighbours(Point p)
        {
            yield return new Point(p.X - 0, p.Y - 1);
            yield return new Point(p.X + 1, p.Y - 1);
            yield return new Point(p.X + 1, p.Y + 0);
            yield return new Point(p.X + 1, p.Y + 1);
            yield return new Point(p.X + 0, p.Y + 1);
            yield return new Point(p.X - 1, p.Y + 1);
            yield return new Point(p.X - 1, p.Y - 0);
            yield return new Point(p.X - 1, p.Y - 1);
        }

        public static char Grid(char[,] grid, Point p) {
            var x = p.X;
            var y = p.Y;
            var height = grid.GetLength(0);
            var width = grid.GetLength(1);
            return (0 <= x && x < width && 0 <= y && y < height) ? grid[y, x] : '\0';
        }

        static void Main(string[] args)
        {
            var border = FindBorder(TestGrid, TestStart, TestInside, TestOutside);

            var points = Enumerable.Range(0, TestHeight)
                                   .SelectMany(y => Enumerable.Range(0, TestWidth)
                                                              .Select(x => new Point(x, y)));

            foreach (var p in points) {
                Console.Write(border.Contains(p) ? '*' : Grid(TestGrid, p));
                if (p.X + 1 == TestWidth) Console.WriteLine();
            }

            Console.ReadLine();
        }

        private static readonly char[,] TestGrid = new char[,] {
            { '1', '1', '1', '1', '1', '1', '1', '2', '2', '2', '2' }, 
            { '1', '1', '1', '1', '1', '2', '2', '2', '2', '2', '2' }, 
            { '1', '1', '1', '1', '2', '2', '2', '2', '2', '2', '2' }, 
            { '1', '1', '1', '1', '2', '2', '2', '2', '2', '2', '2' }, 
            { '1', '1', '1', '1', '1', '1', '2', '2', '2', '2', '2' }, 
            { '1', '1', '1', '1', '1', '1', '3', '3', '3', '2', '2' }, 
            { '1', '1', '3', '3', '3', '3', '3', '3', '3', '3', '3' }
        };
        private static readonly Point TestStart = new Point(3, 3);
        private static readonly Point TestAdjacent = new Point(4, 3);
        private static readonly char TestInside = Grid(TestGrid, TestStart);
        private static readonly char TestOutside = Grid(TestGrid, TestAdjacent);
        private static readonly int TestWidth = TestGrid.GetLength(1);
        private static readonly int TestHeight = TestGrid.GetLength(0);
    }
}

Answer 3

Вот несколько мыслей и начало алгоритма:

Найти контур области одинакового цвета легче, чем найти границу, особенно когда граница на самом деле не является "двоичной" (т. Е. Только 2 цвета), как это выглядит на вашем изображении.

Поиск смежных частей двух контуров не очень сложен. Для каждой точки контура A найдите ближайшую точку контура B. Если расстояние |A-B| < X точка на полпути между А и В находится на границе. (X зависит от нечеткости вашей границы)

Если вы сможете заставить своих пользователей щелкать дважды по обе стороны границы, это было бы здорово. Если вы настаиваете на одном щелчке, найдите две самые большие области в радиусе X вокруг точки нажатия.

Найти контур области не сложно:

1. взять точку (x,y) начать, выбрать направление (dx,dy)=(1,0) начать
2. взять цвет C точки (x,y) который будет цветом для отслеживания
3. бежать x+=dx,y+=dy пока в (x+dx,y+dy) у вас есть другой цвет и вы находитесь на границе
4. заглянуть в (x+dx,y+dy), если это не тот же цвет C, вы попадаете на границу: поверните налево и переходите к 4.
5. x+=dx, y+=dy т.е. сделать шаг
6. запись (x,y) как часть границы
7. если ( x==xstart && y==ystart ) ты сделал
8. повернуть направо и перейти к 4.

поворот налево означает: (dx',dy') = (dy,-dx), revolutions++

повернуть направо означает: (dx',dy') = (-dy,dx), revolutions--

revolutions будет в конечном итоге положительным или отрицательным, в зависимости от направления трассировки (внутри / снаружи)

Есть один угловой случай, в котором это повторяется бесконечно, а именно, когда вы начинаете в области 1 пикселя. Это легко проверить. Кроме того, вы можете проверить х / у границы. "Один и тот же цвет" и "другой цвет", конечно, также могут быть реализованы как некоторый предел цветового расстояния (т.е. |(r,g,b)-(R,G,B)|<D)

Отказ от ответственности - это работающий, но простой, медленный алгоритм, который я разработал один раз без бремени каких-либо соответствующих знаний или опыта.

Answer 4

Хорошие ресурсы для этого материала здесь: обнаружение краевых пикселей с помощью алгоритма марширующих квадратов и в википедии (если эта ссылка исчезнет).