Алгоритм обратного распространения слишком быстро сходится к плохим результатам
Я пытаюсь реализовать алгоритм обратного распространения для многослойной нейронной сети с прямой связью, но у меня возникают проблемы с тем, чтобы он сходился к хорошим результатам. Причина в том, что градиентный спуск застревает на пластине среднеквадратичной ошибки.
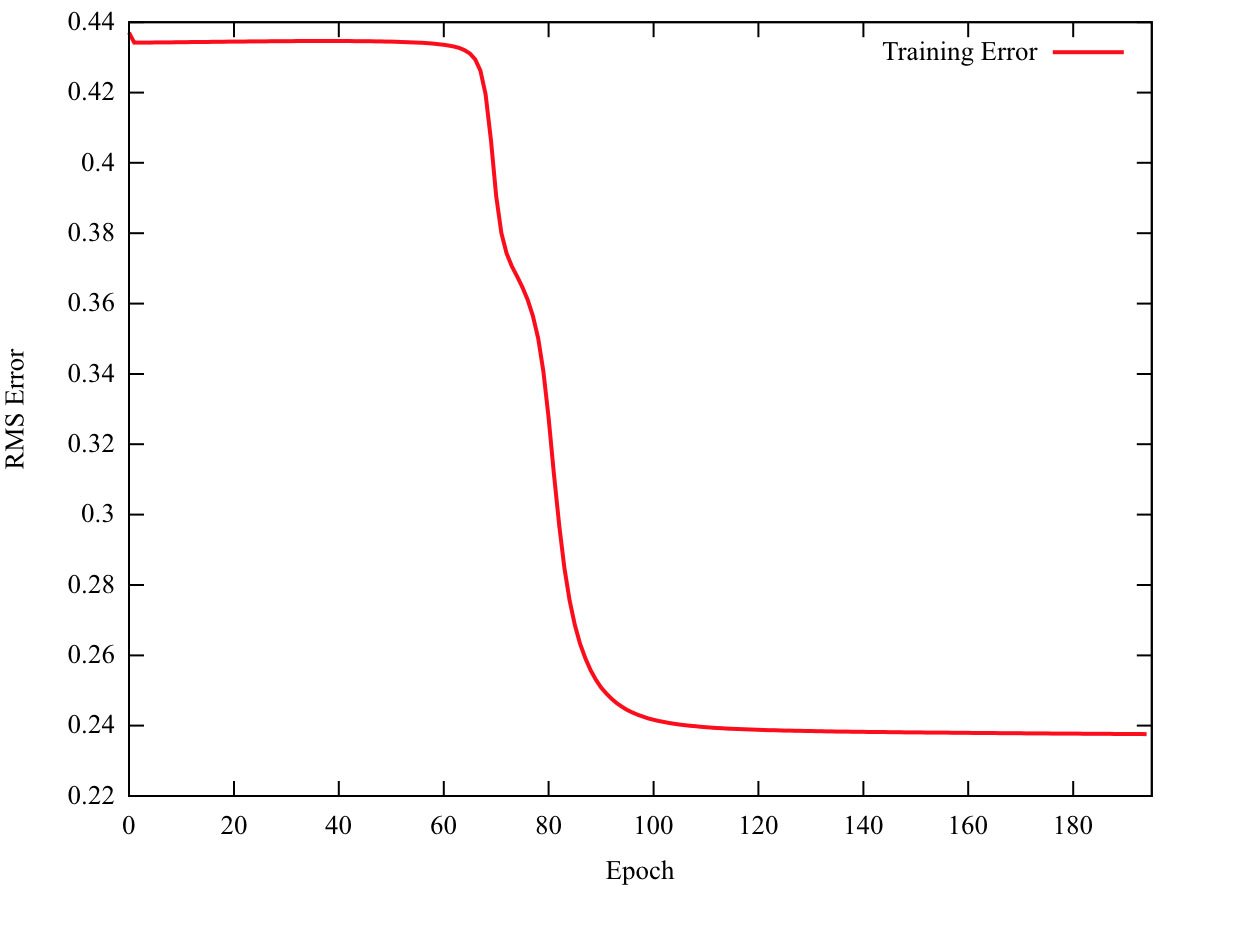
Как вы можете видеть на графике, среднеквадратичное значение очень мало изменяется в первые 70 эпох или около того. Поэтому градиентный спуск вещей его нашел минимум и остановился. Чтобы исправить это, я установил требование, чтобы среднеквадратичная ошибка была ниже 0,3, а скорость изменения была ниже заданного значения. Однако я не думаю, что это хорошо, так как считаю, что с моей реализацией что-то не так.
Ниже приведен код рубина:
def train eta, criteria
rms = 1
old_rms = 0
rms_window = Array.new 20, 0
new_avg = 10
old_avg = 0
diff = 100
epoch = 0
@data[:training].shuffle!
while (diff > criteria || rms > 0.3) do
#while (diff > criteria) do
rms = 0
old_avg = new_avg
new_avg = 0
classification_error = 0
sample_num = 0
@data[:training].each_with_index do |s, s_i|
# Forward Propagation
inputs = [1, s[1], s[2]]
@hidden_layers.each_with_index do |hl, hl_i|
outputs = Array.new
# Bias Term
outputs << 1
# Compute the output for each neuron
hl.each do |p|
outputs << p.compute_output(inputs)
end
inputs = outputs
end
# Compute System Outputs
outputs = Array.new
@outputs.each do |p|
outputs << p.compute_output(inputs)
end
# Comput Errors
errors = Array.new
desired = @desired_values[s[0]-1]
@outputs.length.times do |x|
errors[x] = desired[x] - outputs[x]
rms += errors[x]**2
end
decision = outputs.each_with_index.max[1]
if decision+1 != s[0]
classification_error += 1
end
# Back Propagation
gradients = Array.new
local_gradient = Array.new
next_layer = Array.new
@outputs.each_with_index do |o, i|
local_gradient << errors[i] * o.activation_prime(o.output)
o.weights.length.times do |x|
o.weights[x] += eta * local_gradient[i] * o.inputs[x]
end
end
gradients << local_gradient
next_layer = @outputs
@hidden_layers.reverse_each do |hl|
local_gradient = Array.new
hl.each do |p|
gradient = 0
gradients.last.each_with_index do |g, i|
gradient += g * next_layer[i].weights[p.index+1]
end
gradient *= p.activation_prime(p.output)
local_gradient << gradient
p.weights.each_index do |x|
p.weights[x] += eta * gradient * p.inputs[x]
end
end
gradients << local_gradient
next_layer = hl
end
if s_i == 0
#puts "Epoch: #{epoch}\nOutputs: #{outputs}\nGradients:\n#{gradients[0]}\n#{gradients[1]}\n#{gradients[2]}\n\n"
#puts "Epoch #{epoch}\nError: #{errors}\nSE: #{rms}"
end
end
rms = Math::sqrt(rms / (@data[:training].length * 4))
rms_window[0] = rms
rms_window.rotate!
rms_window.each do |x|
new_avg += x
end
new_avg /= 20
diff = (new_avg - old_avg).abs
@rms << rms
epoch += 1
if classification_error == 0
break
end
#puts "RMS: #{rms}\tDiff: \t#{diff}\tClassification: #{classification_error}\n\n"
end
self.rms_plot "Plot"
self.grid_eval "Test", 250
end
Показанный график для сети с 2 скрытыми слоями с 5 нейронами в каждом скрытом слое. Есть 2 входа и 4 выхода. Возможно, это нормальное поведение, но мне кажется, что-то не так. Любая помощь будет принята с благодарностью.
2 ответа
Есть много параметров, которые необходимо настроить, чтобы заставить работать многослойную нейронную сеть. Основываясь на моем эксперименте, мои первые предложения:
1 - дайте ему небольшой набор синтезированных данных и запустите детский проект, чтобы посмотреть, работает ли фреймворк.
2- Используйте более выпуклую функцию стоимости. Не существует функции, которая гарантирует выпуклость, но есть много функций, которые являются более выпуклыми, чем RMS.
3- Попробуйте масштабировать входные данные в (-1,1) и выводить данные в (0,1).
4- Попробуйте разные значения для скорости обучения.
В дополнение к тому, что уже было сказано:
немного изменить диапазон начальных весов (например, 0 - 1)
убедитесь, что ваши входные данные правильно нормированы - я упал, это не может быть сказано достаточно часто
измените скорость обучения, начните с sth, например, 0,05, и продолжайте увеличивать / уменьшать небольшими шагами (если вы обнаружите, что изменение скорости обучения слишком сильно влияет на производительность сети, возможно, вы не нормализовали входные данные должным образом)
перемешивать входные данные перед каждой эпохой
попробуйте использовать импульс (это, по сути, означает, что скорость обучения увеличивается, когда градиент крутой, уменьшается, если он становится более плоским), это часто помогает перепрыгнуть через локальные оптимумы
попробуйте использовать регуляризацию
поэкспериментируйте со структурой (добавьте еще один скрытый слой, увеличьте количество единиц в скрытом слое)