Расчет коэффициента Джини в Python/ NumPy

Question

Я рассчитываю коэффициент Джини (похож на: Python - расчет коэффициента Джини с использованием Numpy), но я получаю странный результат. для равномерного распределения, отобранного из np.random.rand()коэффициент Джини равен 0,3, но я бы ожидал, что он будет близок к 0 (идеальное равенство). что здесь не так?

def G(v):
    bins = np.linspace(0., 100., 11)
    total = float(np.sum(v))
    yvals = []
    for b in bins:
        bin_vals = v[v <= np.percentile(v, b)]
        bin_fraction = (np.sum(bin_vals) / total) * 100.0
        yvals.append(bin_fraction)
    # perfect equality area
    pe_area = np.trapz(bins, x=bins)
    # lorenz area
    lorenz_area = np.trapz(yvals, x=bins)
    gini_val = (pe_area - lorenz_area) / float(pe_area)
    return bins, yvals, gini_val

v = np.random.rand(500)
bins, result, gini_val = G(v)
plt.figure()
plt.subplot(2, 1, 1)
plt.plot(bins, result, label="observed")
plt.plot(bins, bins, '--', label="perfect eq.")
plt.xlabel("fraction of population")
plt.ylabel("fraction of wealth")
plt.title("GINI: %.4f" %(gini_val))
plt.legend()
plt.subplot(2, 1, 2)
plt.hist(v, bins=20)

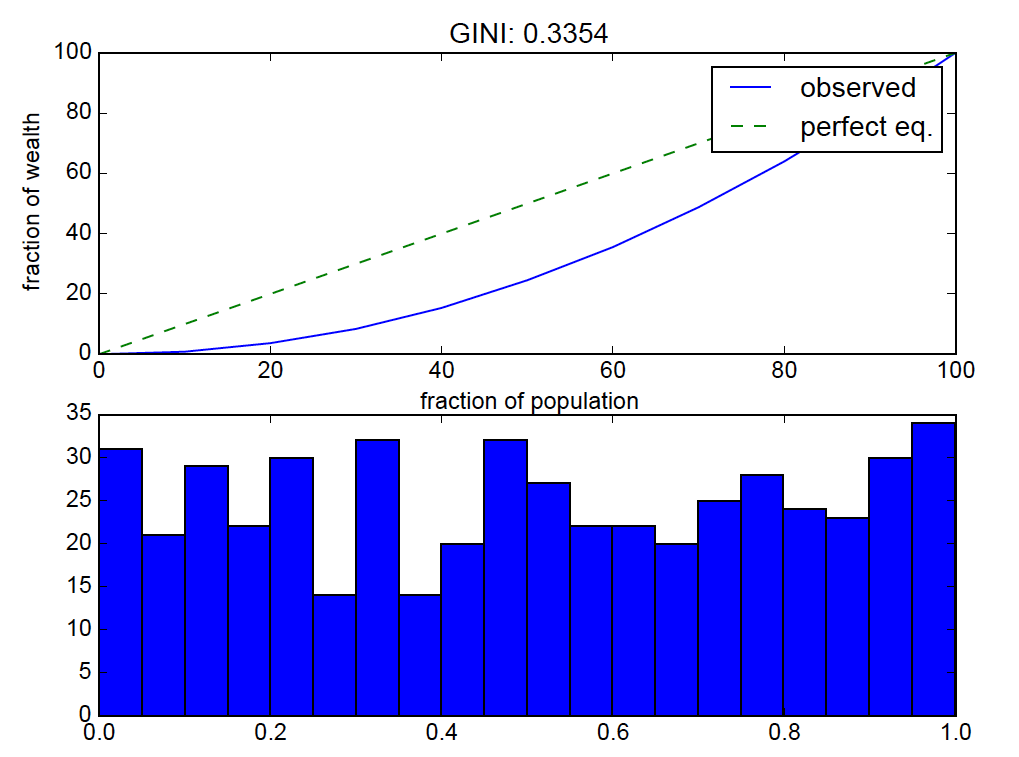
для данного набора чисел приведенный выше код вычисляет долю от общих значений распределения, которые находятся в каждом процентном бине.

результат:

равномерное распределение должно быть близко к "идеальному равенству", поэтому изгиб кривой Лоренца выключен.

Answer 1

Этого следовало ожидать. Случайная выборка из равномерного распределения не приводит к однородным значениям (то есть значениям, которые все относительно близки друг к другу). С помощью небольшого исчисления можно показать, что ожидаемое значение (в статистическом смысле) коэффициента Джини для выборки из равномерного распределения на [0, 1] составляет 1/3, поэтому получение значений около 1/3 для Данный образец является разумным.

Вы получите более низкий коэффициент Джини с такой выборкой, как v = 10 + np.random.rand(500), Все эти значения близки к 10,5; относительный разброс ниже, чем образец v = np.random.rand(500), На самом деле, ожидаемое значение коэффициента Джини для образца base + np.random.rand(n) 1/(6* база + 3).

Вот простая реализация коэффициента Джини. Он использует тот факт, что коэффициент Джини составляет половину относительной средней абсолютной разницы.

def gini(x):
    # (Warning: This is a concise implementation, but it is O(n**2)
    # in time and memory, where n = len(x).  *Don't* pass in huge
    # samples!)

    # Mean absolute difference
    mad = np.abs(np.subtract.outer(x, x)).mean()
    # Relative mean absolute difference
    rmad = mad/np.mean(x)
    # Gini coefficient
    g = 0.5 * rmad
    return g

Вот коэффициент Джини для нескольких образцов вида v = base + np.random.rand(500):

In [80]: v = np.random.rand(500)

In [81]: gini(v)
Out[81]: 0.32760618249832563

In [82]: v = 1 + np.random.rand(500)

In [83]: gini(v)
Out[83]: 0.11121487509454202

In [84]: v = 10 + np.random.rand(500)

In [85]: gini(v)
Out[85]: 0.01567937753659053

In [86]: v = 100 + np.random.rand(500)

In [87]: gini(v)
Out[87]: 0.0016594595244509495

Answer 2

Немного более быстрая реализация (с использованием векторизации numpy и вычислением каждой разницы только один раз):

def gini_coefficient(x):
    """Compute Gini coefficient of array of values"""
    diffsum = 0
    for i, xi in enumerate(x[:-1], 1):
        diffsum += np.sum(np.abs(xi - x[i:]))
    return diffsum / (len(x)**2 * np.mean(x))

Заметка: x должен быть массивом numpy.

Answer 3

Коэффициент Джини - это площадь под кривой Лоренца, обычно рассчитываемая для анализа распределения доходов населения. https://github.com/oliviaguest/gini предоставляет простую реализацию того же самого с использованием Python.

Answer 4

Небольшая заметка об исходной методологии:

При вычислении коэффициентов Джини непосредственно из площадей под кривыми с помощью np.traps или другого метода интегрирования первое значение кривой Лоренца должно быть 0, чтобы учитывалась область между началом координат и вторым значением. Следующие изменения вG(v) почини это:

yvals = [0]
for b in bins[1:]:

Я также обсудил эту проблему в этом ответе, где включение источника в эти вычисления дает эквивалентный ответ на использование других обсуждаемых здесь методов (которые не требуют добавления 0).

Короче говоря, при вычислении коэффициентов Джини напрямую с помощью интегрирования вам нужно начинать с начала координат. При использовании других методов, обсуждаемых здесь, в этом нет необходимости.

Answer 5

Были некоторые проблемы с предыдущими реализациями. Они никогда не давали индекс Джини = 1 для совершенно разреженных данных.

пример:

      def gini_coefficient(x):
        """Compute Gini coefficient of array of values"""
        diffsum = 0
        for i, xi in enumerate(x[:-1], 1):
            diffsum += np.sum(np.abs(xi - x[i:]))
        return diffsum / (len(x)**2 * np.mean(x))
    
    gini_coefficient(np.array([0, 0, 1]))

дает ответ 0,666666. Это происходит из-за подразумеваемой «схемы интеграции», которую он использует.

Вот еще один вариант, который обходит эту проблему, хотя и требует больших вычислительных ресурсов:

      import numpy as np
from scipy.interpolate import interp1d

def gini(v, n_new = 1000):
    """Compute Gini coefficient of array of values"""
    v_abs = np.sort(np.abs(v))
    cumsum_v = np.cumsum(v_abs)
    n = len(v_abs)
    vals = np.concatenate([[0], cumsum_v/cumsum_v[-1]])
    x = np.linspace(0, 1, n+1)
    f = interp1d(x=x, y=vals, kind='previous')
    xnew = np.linspace(0, 1, n_new+1)
    dx_new = 1/(n_new)
    vals_new = f(xnew)
    return 1 - 2 * np.trapz(y=vals_new, x=xnew, dx=dx_new)

gini(np.array([0, 0, 1]))

это дает выход 0,999, что ближе к тому, что нужно иметь =)

Answer 6

Обратите внимание, что индекс gini в настоящее время присутствует в skbio.diversity.alpha как gini_index. Это может дать немного другой результат с примерами, упомянутыми выше.

Answer 7

Вы получаете правильный ответ. Коэффициент Джини равномерного распределения равен 0 не «совершенному равенству», а (b-a) / (3*(b+a)). В твоем случае, b = 1, а также a = 0, так Gini = 1/3.

Единственными распределениями с полным равенством являются дельты Кронекера и Дирака. Помните, что равенство означает «все равно», а не «все равновероятны».

Answer 8

Вот реализация, которая лучше подходит для небольших целочисленных значений. Он сохраняет все вычисления с плавающей запятой на конец и, таким образом, является более точным. Не предназначен для больших входов.

      def gini_coefficient(x):
    x = sorted(x)
    n = len(x)
    s = sum(x)
    d = n * s
    G = sum(xi * (n - i) for i, xi in enumerate(x))
    return (d + s - 2 * G) / d