Python - расчет коэффициента Джини с использованием Numpy
Я новичок, во-первых, только начал изучать Python, и я пытаюсь написать код для расчета индекса Джини для фальшивой страны. Я придумал следующее:
GDP = (653200000000)
A = (0.49 * GDP) / 100 # Poorest 10%
B = (0.59 * GDP) / 100
C = (0.69 * GDP) / 100
D = (0.79 * GDP) / 100
E = (1.89 * GDP) / 100
F = (2.55 * GDP) / 100
G = (5.0 * GDP) / 100
H = (10.0 * GDP) / 100
I = (18.0 * GDP) / 100
J = (60.0 * GDP) / 100 # Richest 10%
# Divide into quintiles and total income within each quintile
Q1 = float(A + B) # lowest quintile
Q2 = float(C + D) # second quintile
Q3 = float(E + F) # third quintile
Q4 = float(G + H) # fourth quintile
Q5 = float(I + J) # fifth quintile
# Calculate the percent of total income in each quintile
T1 = float((100 * Q1) / GDP) / 100
T2 = float((100 * Q2) / GDP) / 100
T3 = float((100 * Q3) / GDP) / 100
T4 = float((100 * Q4) / GDP) / 100
T5 = float((100 * Q5) / GDP) / 100
TR = float(T1 + T2 + T3 + T4 + T5)
# Calculate the cumulative percentage of household income
H1 = float(T1)
H2 = float(T1+T2)
H3 = float(T1+T2+T3)
H4 = float(T1+T2+T3+T4)
H5 = float(T1+T2+T3+T4+T5)
# Magic! Using numpy to calculate area under Lorenz curve.
# Problem might be here?
import numpy as np
from numpy import trapz
# The y values. Cumulative percentage of incomes
y = np.array([Q1,Q2,Q3,Q4,Q5])
# Compute the area using the composite trapezoidal rule.
area_lorenz = trapz(y, dx=5)
# Calculate the area below the perfect equality line.
area_perfect = (Q5 * H5) / 2
# Seems to work fine until here.
# Manually calculated Gini using the values given for the areas above
# turns out at .58 which seems reasonable?
Gini = area_perfect - area_lorenz
# Prints utter nonsense.
print Gini
Результат Gini = area_perfect - area_lorenz просто не имеет смысла. Я вынул значения, заданные переменными области, и сделал математику от руки, и это получилось довольно хорошо, но когда я пытаюсь заставить программу сделать это, это дает мне полностью??? значение (-1,7198...). Что мне не хватает? Может ли кто-нибудь указать мне правильное направление?
Спасибо!
1 ответ
Первая проблема заключается в неправильном факторинге уравнения для коэффициента Джини:
gini = (площадь между кривой Лоренца и полным равенством) / (площадь при полном равенстве)
Вы не включили знаменатель в свои вычисления, а также используете неверное уравнение для площади под линией равенства (см. Код метода, использующего np.linspace и np.trapz).
Также существует проблема, заключающаяся в том, что отсутствует первая точка кривой Лоренца (вам нужно начинать с 0, а не с доли первого квинтиля). Хотя площадь под кривой Лоренца мала между 0 и первым квинтилем, ее отношение к площади под линией равенства после ее расширения довольно велико.
Ниже приводится эквивалентный ответ на методы, приведенные в ответах на этот вопрос:
import numpy as np
GDP = 653200000000 # you don't actually need this value
# Decile percents of global GDP
gdp_decile_percents = [0.49, 0.59, 0.69, 0.79, 1.89, 2.55, 5.0, 10.0, 18.0, 60.0]
print('Percents sum to 100:', sum(gdp_decile_percents) == 100)
gdp_decile_shares = [i/100 for i in gdp_decile_percents]
# Convert to quintile shares of total GDP
gdp_quintile_shares = [(gdp_decile_shares[i] + gdp_decile_shares[i+1]) for i in range(0, len(gdp_decile_shares), 2)]
# Insert 0 for the first value in the Lorenz curve
gdp_quintile_shares.insert(0, 0)
# Cumulative sum of shares (Lorenz curve values)
shares_cumsum = np.cumsum(a=gdp_quintile_shares, axis=None)
# Perfect equality line
pe_line = np.linspace(start=0.0, stop=1.0, num=len(shares_cumsum))
area_under_lorenz = np.trapz(y=shares_cumsum, dx=1/len(shares_cumsum))
area_under_pe = np.trapz(y=pe_line, dx=1/len(shares_cumsum))
gini = (area_under_pe - area_under_lorenz) / area_under_pe
print('Gini coefficient:', gini)
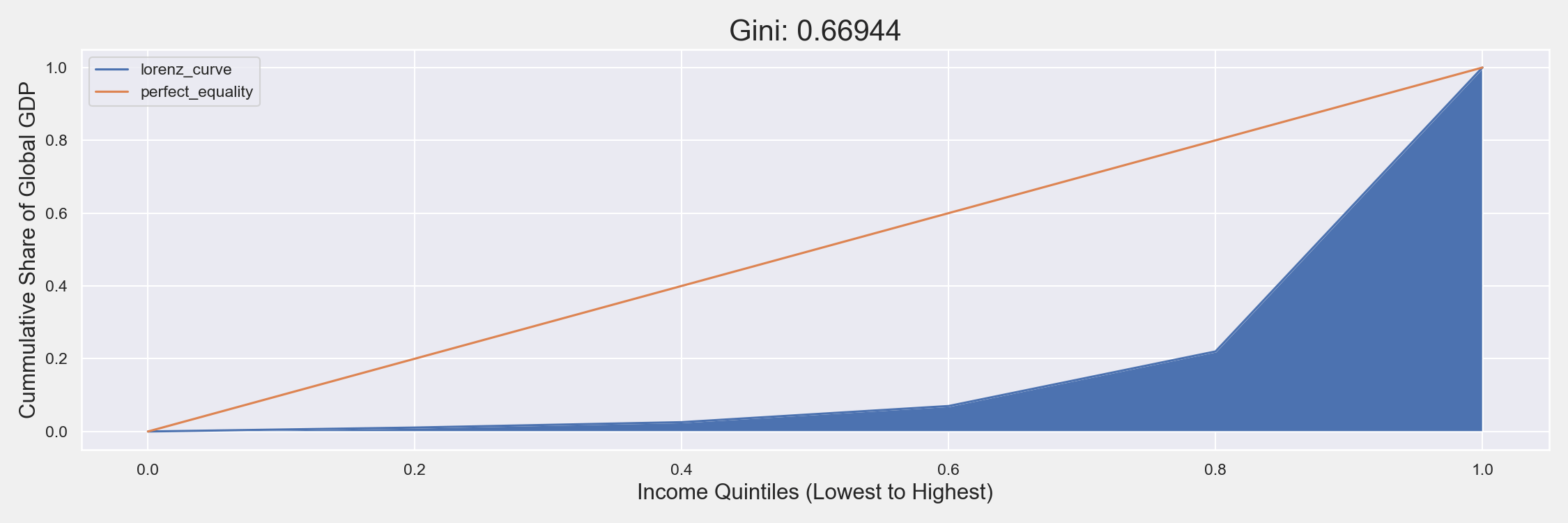
Площади, рассчитанные с помощью np.trapzдают коэффициент 0,67. Значение, рассчитанное без первой точки кривой Лоренца и с использованием trapz, составило 0,59. Наш расчет глобального неравенства теперь примерно равен расчету, предоставляемому методами в вопросе, связанном выше (вам не нужно добавлять 0 в списки / массивы этих методов). Обратите внимание, что использование scipy.integrate.simps дает 0,69, что означает, что методы в другом вопросе больше совпадают с трапецеидальной, чем с интеграцией Симпсона.
Вот сюжет, в который входит plt.fill_between раскрасить под кривой Лоренца:
from matplotlib import pyplot as plt
plt.plot(pe_line, income_cumsum, label='lorenz_curve')
plt.plot(pe_line, pe_line, label='perfect_equality')
plt.fill_between(pe_line, income_cumsum)
plt.title('Gini: {}'.format(gini), fontsize=20)
plt.ylabel('Cummulative Share of Global GDP', fontsize=15)
plt.xlabel('Income Quintiles (Lowest to Highest)', fontsize=15)
plt.legend()
plt.tight_layout()
plt.show()
Stardust.
Ваша проблема не с numpy.trapz; это с 1) вашим определением распределения идеального равенства и 2) нормализацией коэффициента Джини.
Во-первых, вы определили идеальное распределение равенства как Q5*H5/2, что составляет половину произведения дохода пятого квинтиля и совокупного процента (1,0). Я не уверен, что это число должно представлять.
Во-вторых, вы должны нормализовать по области под идеальным распределением равенства; то есть:
Джини = (площадь при идеальном равенстве - площадь под Лоренцем)/(площадь при идеальном равенстве)
Вам не нужно беспокоиться об этом, если вы определяете идеальную кривую равенства, чтобы иметь площадь 1, но это хорошая гарантия, если в вашем определении идеальной кривой равенства есть ошибка.
Чтобы решить обе эти проблемы, я определил идеальную кривую равенства numpy.linspace, Первое преимущество этого заключается в том, что вы можете использовать свойства реального дистрибутива, чтобы определить его таким же образом. Другими словами, используете ли вы квартили, квинтили или децили, CDF с идеальным равенством (y_pe ниже) будет иметь правильную форму. Второе преимущество состоит в том, что вычисление его площади выполняется с numpy.trapz также немного параллелизма, который делает код более легким для чтения и защищает от ошибочных вычислений.
import numpy as np
from matplotlib import pyplot as plt
from numpy import trapz
GDP = (653200000000)
A = (0.49 * GDP) / 100 # Poorest 10%
B = (0.59 * GDP) / 100
C = (0.69 * GDP) / 100
D = (0.79 * GDP) / 100
E = (1.89 * GDP) / 100
F = (2.55 * GDP) / 100
G = (5.0 * GDP) / 100
H = (10.0 * GDP) / 100
I = (18.0 * GDP) / 100
J = (60.0 * GDP) / 100 # Richest 10%
# Divide into quintiles and total income within each quintile
Q1 = float(A + B) # lowest quintile
Q2 = float(C + D) # second quintile
Q3 = float(E + F) # third quintile
Q4 = float(G + H) # fourth quintile
Q5 = float(I + J) # fifth quintile
# Calculate the percent of total income in each quintile
T1 = float((100 * Q1) / GDP) / 100
T2 = float((100 * Q2) / GDP) / 100
T3 = float((100 * Q3) / GDP) / 100
T4 = float((100 * Q4) / GDP) / 100
T5 = float((100 * Q5) / GDP) / 100
TR = float(T1 + T2 + T3 + T4 + T5)
# Calculate the cumulative percentage of household income
H1 = float(T1)
H2 = float(T1+T2)
H3 = float(T1+T2+T3)
H4 = float(T1+T2+T3+T4)
H5 = float(T1+T2+T3+T4+T5)
# The y values. Cumulative percentage of incomes
y = np.array([H1,H2,H3,H4,H5])
# The perfect equality y values. Cumulative percentage of incomes.
y_pe = np.linspace(0.0,1.0,len(y))
# Compute the area using the composite trapezoidal rule.
area_lorenz = np.trapz(y, dx=5)
# Calculate the area below the perfect equality line.
area_perfect = np.trapz(y_pe, dx=5)
# Seems to work fine until here.
# Manually calculated Gini using the values given for the areas above
# turns out at .58 which seems reasonable?
Gini = (area_perfect - area_lorenz)/area_perfect
print Gini
plt.plot(y,label='lorenz')
plt.plot(y_pe,label='perfect_equality')
plt.legend()
plt.show()