Как "сгладить" или "индексировать" 3D-массив в 1D-массиве?
Я пытаюсь объединить 3D-массив в 1D-массив для "чанковой" системы в моей игре. Это трехмерная блочная игра, и я хочу, чтобы система чанков была практически идентична системе Minecraft (однако это ни в коем случае не клон Minecraft). В моих предыдущих 2D-играх я обращался к сглаженному массиву по следующему алгоритму:
Tiles[x + y * WIDTH]
Однако это, очевидно, не работает с 3D, так как в нем отсутствует ось Z. Я понятия не имею, как реализовать такой алгоритм в 3D-пространстве. Ширина, высота и глубина - все константы (а ширина такая же, как высота).
Это просто x + y*WIDTH + Z*DEPTH? Я довольно плохо разбираюсь в математике, и я только начинаю 3D-программирование, поэтому я довольно растерялся: |
PS. Причина этого в том, что я довольно много зацикливаюсь и получаю данные по индексу. Я знаю, что одномерные массивы быстрее многомерных (по причинам, которые я не могу вспомнить:P). Несмотря на то, что в этом нет необходимости, я хочу максимально возможной производительности:)
14 ответов
Алгоритм в основном такой же. Если у вас есть 3D-массив Original[HEIGHT, WIDTH, DEPTH] тогда вы могли бы превратить его в Flat[HEIGHT * WIDTH * DEPTH] от
Flat[x + WIDTH * (y + DEPTH * z)] = Original[x, y, z]
Кроме того, вы должны предпочесть массивы массивов по сравнению с многомерными массивами в.NET. Различия в производительности значительны
Вот решение на Java, которое дает вам оба:
- от 3D до 1D
- от 1D до 3D
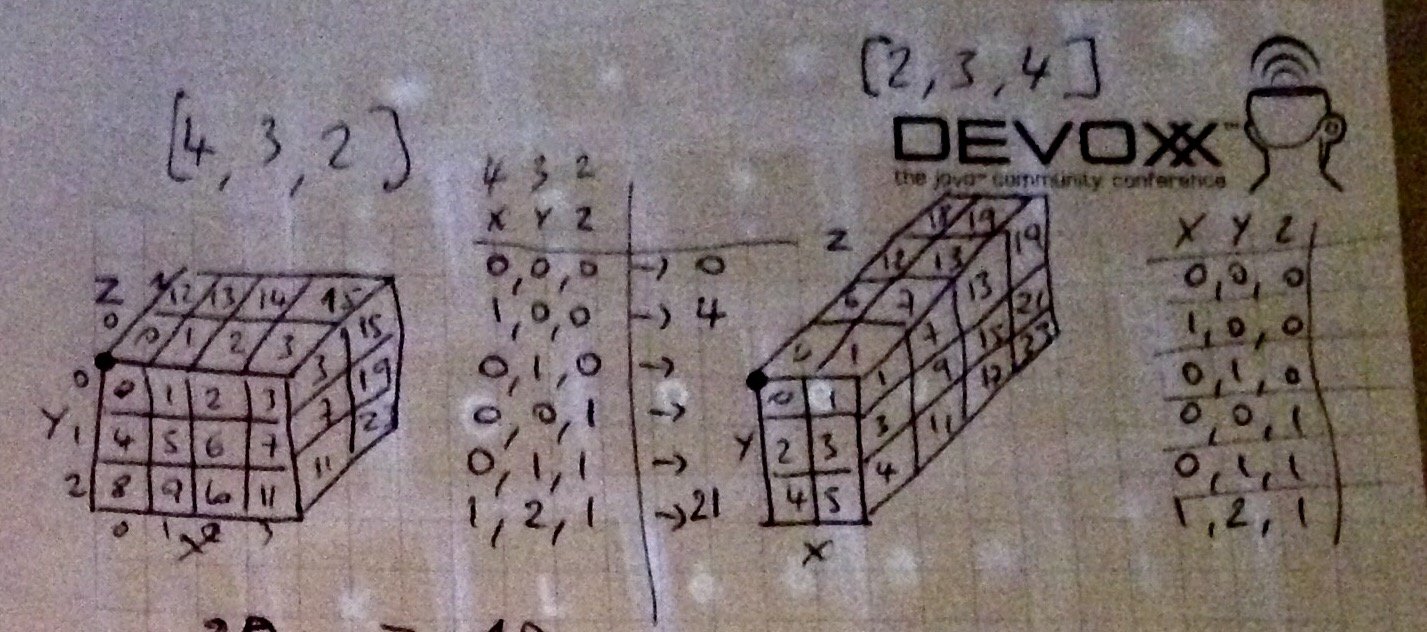
Ниже приведена графическая иллюстрация пути, который я выбрал для прохождения трехмерной матрицы, ячейки пронумерованы в порядке их обхода:
Функции преобразования:
public int to1D( int x, int y, int z ) {
return (z * xMax * yMax) + (y * xMax) + x;
}
public int[] to3D( int idx ) {
final int z = idx / (xMax * yMax);
idx -= (z * xMax * yMax);
final int y = idx / xMax;
final int x = idx % xMax;
return new int[]{ x, y, z };
}
Я думаю, что вышесказанное нуждается в небольшой коррекции. Допустим, у вас есть ВЫСОТА 10, а ШИРИНА 90, одномерный массив будет 900. По приведенной выше логике, если вы находитесь на последнем элементе массива 9 + 89*89, очевидно, что это больше, чем 900. Правильный алгоритм:
Flat[x + HEIGHT* (y + WIDTH* z)] = Original[x, y, z], assuming Original[HEIGHT,WIDTH,DEPTH]
По иронии судьбы, если вы ВЫСОТА> ШИРИНА, вы не будете испытывать переполнение, просто завершите помешанные результаты;)
x + y*WIDTH + Z*WIDTH*DEPTH, Визуализируйте его как прямоугольное тело: сначала вы пройдете вдоль xзатем каждый y это "линия" width шаги длинные, и каждый z это "самолет" WIDTH*DEPTH шаги в области.
Ты почти там. Вам нужно умножить Z на WIDTH а также DEPTH:
Tiles[x + y*WIDTH + Z*WIDTH*DEPTH] = elements[x][y][z]; // or elements[x,y,z]
TL;DR
Правильный ответ может быть написан различными способами, но мне больше всего нравится, когда его можно написать так, чтобы его было легко понять и визуализировать. Вот точный ответ:
(width * height * z) + (width * y) + x
TS; DR
Визуализируйте это:
someNumberToRepresentZ + someNumberToRepresentY + someNumberToRepresentX
someNumberToRepresentZ указывает на какую матрицу мы находимся (depth). Чтобы узнать, на какой матрице мы находимся, мы должны знать, насколько велика каждая матрица. Матрица имеет размер 2d как width * height, просто. Вопрос, который нужно задать: "Сколько матриц до матрицы, на которой я нахожусь?" Ответ z:
someNumberToRepresentZ = width * height * z
someNumberToRepresentY указывает на какую строку мы находимся (height). Чтобы узнать, в какой строке мы находимся, мы должны знать, насколько велика каждая строка: каждая строка имеет размер 1d и имеет размер width, Вопрос, который нужно задать, это "сколько строк перед строкой, в которой я нахожусь?". Ответ y:
someNumberToRepresentY = width * y
someNumberToRepresentX указывает на какой столбец мы находимся (width). Чтобы узнать, по какой колонке мы находимся, мы просто используем x:
someNumberToRepresentX = x
Наша визуализация тогда
someNumberToRepresentZ + someNumberToRepresentY + someNumberToRepresentX
становится
(width * height * z) + (width * y) + x
Прямые и обратные преобразования Самуэля Керриена, приведенные выше, почти верны. Более краткие (основанные на R) карты преобразования включены ниже с примером ("a %% b" - это оператор по модулю, представляющий остаток от деления a на b):
dx=5; dy=6; dz=7 # dimensions
x1=1; y1=2; z1=3 # 3D point example
I = dx*dy*z1+dx*y1+x1; I # corresponding 2D index
# [1] 101
x= I %% dx; x # inverse transform recovering the x index
# [1] 1
y = ((I - x)/dx) %% dy; y # inverse transform recovering the y index
# [1] 2
z= (I-x -dx*y)/(dx*dy); z # inverse transform recovering the z index
# [1] 3
Обратите внимание на операторы деления (/) и модуля (%%).
Правильный алгоритм:
Flat[ x * height * depth + y * depth + z ] = elements[x][y][z]
where [WIDTH][HEIGHT][DEPTH]
Чтобы лучше понять описание трехмерного массива в одномерном массиве (я думаю, что глубина в лучшем ответе означает размер Y)
IndexArray = x + y * InSizeX + z * InSizeX * InSizeY;
IndexArray = x + InSizeX * (y + z * InSizeY);
M [x][y][z] = данные [xYZ + yZ + z]
x-picture:
0-YZ
.
.
x-YZ
y-picture
0-Z
.
.
.
y-Z
summing up, it should be : targetX*YZ + targetY*Z + targetZ
Версия Python:
from operator import mul
from functools import reduce
def idx_1D(target, shape):
idx = 0
for i, digit in enumerate(target):
coeff = reduce(mul, shape[i + 1 :]) if i < len(shape) - 1 else 1
idx += digit * coeff
return idx
Ответ Сэмюэля Керриена на python:
def to1D(crds,dims):
x,y,z=crds
xMax,yMax,zMax=dims
return (z * xMax * yMax) + (y * xMax) + x
def to3D(idx,dims):
xMax,yMax,zMax=dims
z = idx // (xMax * yMax)
idx -= (z * xMax * yMax)
y = idx // xMax
x = idx % xMax
return x, y, z
ВотC#реализация матрицы общего ранга. Данные хранятся в 1D-массиве, а функцияint GetIndex(int,int,int...)находит индекс в одномерном массиве, который соответствует индексам тензора n-го ранга. Обратное называетсяint[] GetIndexes(int)
Код также поддерживает как упорядочение по столбцам (по умолчанию), так и упорядочение по строкам.
public enum IndexOrdering
{
ColumnMajor,
RowMajor,
}
public class Matrix<T>
{
readonly T[] _data;
readonly int[] _shape;
public Matrix(IndexOrdering ordering, int[] shape)
{
Ordering = ordering;
Rank = shape.Length;
_shape = shape;
Size = shape.Aggregate(1, (s, l) => s * l);
_data = new T[Size];
}
public Matrix(params int[] shape)
: this(IndexOrdering.ColumnMajor, shape) { }
public Matrix(IndexOrdering ordering, int[] shape, T[] data)
: this(ordering, shape)
{
Array.Copy(data, _data, Size);
}
public int Rank { get; }
public int Size { get; }
public IReadOnlyList<int> Shape { get => _shape; }
internal T[] Data { get => _data; }
public IndexOrdering Ordering { get; set; }
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public int GetIndex(params int[] indexes)
{
switch (Ordering)
{
case IndexOrdering.ColumnMajor:
{
int index = 0;
for (int i = 0; i < Rank; i++)
{
index = _shape[i] * index + indexes[i];
}
return index;
}
case IndexOrdering.RowMajor:
{
int index = 0;
for (int i = Rank - 1; i >= 0; i--)
{
index = _shape[i] * index + indexes[i];
}
return index;
}
default:
throw new NotSupportedException();
}
}
public int[] GetIndexes(int index)
{
int[] indexes = new int[Rank];
switch (Ordering)
{
case IndexOrdering.ColumnMajor:
{
for (int i = Rank - 1; i >= 0; i--)
{
// div = index/shape[i]
// indexes[i] = index - shape[i]*div
// index = div
index = Math.DivRem(index, _shape[i], out indexes[i]);
}
return indexes;
}
case IndexOrdering.RowMajor:
{
for (int i = 0; i < Rank; i++)
{
// div = index/shape[i]
// indexes[i] = index - shape[i]*div
// index = div
index = Math.DivRem(index, _shape[i], out indexes[i]);
}
return indexes;
}
default:
throw new NotSupportedException();
}
}
public T this[params int[] indexes]
{
get => _data[GetIndex(indexes)];
set => _data[GetIndex(indexes)] = value;
}
public override string ToString()
{
return $"[{string.Join(",", _data)}]";
}
}
Чтобы протестировать код с матрицей ранга = 3 (3D-матрица), я использовал:
static void Main(string[] args)
{
const int L0 = 4;
const int L1 = 3;
const int L2 = 2;
var A = new Matrix<int>(L0, L1, L2);
Console.WriteLine($"rank(A)={A.Rank}");
Console.WriteLine($"size(A)={A.Size}");
Console.WriteLine($"shape(A)=[{string.Join(",", A.Shape)}]");
int index = 0;
for (int i = 0; i < L0; i++)
{
for (int j = 0; j < L1; j++)
{
for (int k = 0; k < L2; k++)
{
A[i, j, k] = index++;
}
}
}
Console.WriteLine($"A=");
for (int i = 0; i < L0; i++)
{
for (int j = 0; j < L1; j++)
{
Console.Write($"[{i},{j},..] = ");
for (int k = 0; k < L2; k++)
{
Console.Write($"{A[i, j, k]} ");
}
Console.WriteLine();
}
Console.WriteLine();
}
for (int idx = 0; idx < A.Size; idx++)
{
var ixs = A.GetIndexes(idx);
Console.WriteLine($"A[{string.Join(",", ixs)}] = {A.Data[idx]}");
}
}
с выходом
rank(A)=3
size(A)=24
shape(A)=[4,3,2]
A=
[0,0,..] = 0 1
[0,1,..] = 2 3
[0,2,..] = 4 5
[1,0,..] = 6 7
[1,1,..] = 8 9
[1,2,..] = 10 11
[2,0,..] = 12 13
[2,1,..] = 14 15
[2,2,..] = 16 17
[3,0,..] = 18 19
[3,1,..] = 20 21
[3,2,..] = 22 23
A[0,0,0] = 0
A[0,0,1] = 1
A[0,1,0] = 2
A[0,1,1] = 3
A[0,2,0] = 4
A[0,2,1] = 5
A[1,0,0] = 6
A[1,0,1] = 7
...
A[3,1,1] = 21
A[3,2,0] = 22
A[3,2,1] = 23
В случае, если кто-то заинтересован в выравнивании массива nD (2D, 3D, 4D,...) до 1D, я написал приведенный ниже код. Например, если размер массива в разных измерениях хранится в
sizesмножество:
# pseudo code
sizes = {size_x, size_y, size_z,...};
Эта рекурсивная функция дает вам ряд
{1, size_x, size_x*size_y, size_x*size_y*size_z, ...}
// i: number of the term
public int GetCoeff(int i){
if (i==0)
return 1;
return sizes[i-1]*GetCoeff(i-1);
}
Таким образом, мы должны умножить индексы nD на соответствующий им член ряда и просуммировать их, чтобы получить
{ix + iy*size_x + iz*size_x*size_y, ...}:
// indexNd: {ix, iy, iz, ...}
public int GetIndex1d(int[] indexNd){
int sum =0;
for (var i=0; i<indexNd.Length;i++)
sum += indexNd[i]*GetCoeff(i);
return sum;
}
Я предположил, что в этом коде массив nD непрерывен в памяти сначала по x, затем по y, z,.... Так что, вероятно, вы называете свой массив
arr[z,y,x]. Но если вы назовете их по-другому, arr[x,y,z], тогда z — самый быстрый индекс, и нам нравится вычислять
iz + iy*size_z + ix* size_z*size_y. В этом случае приведенная ниже функция дает нам ряд
{1, size_z, size_z*size_y, ...}:
// Dims is dimension of array, like 3 for 3D
public int GetReverseCoeff(int i){
if (i==0)
return 1;
return sizes[Dims-i]*GetReverseCoeff(i-1);
}
Коэффициенты хранятся в правильном порядке:
public void SetCoeffs(){
for (int i=0;i<Dims;i++)
coeffs[Dims-i-1] = GetReverseCoeff(i);
}
Индекс 1D рассчитывается так же, как и раньше, за исключением того, что используется массив coeffs:
// indexNd: {ix, iy, iz, ...}
public int GetIndex1d(int[] indexNd){
int sum =0;
for (var i=0; i<indexNd.Length;i++)
sum += indexNd[i]*coeffs[i];
return sum;
}