Линейное программирование: могу ли я сформулировать цель максимизации нескольких переменных одновременно?
Допустим, у меня есть некоторые переменные и ограничения, проиллюстрированные следующей системой: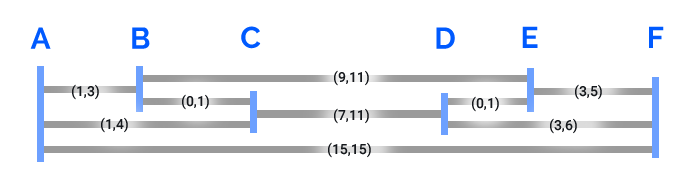 
Серые линии могут растягиваться и уменьшаться на величину, заданную диапазоном над ними. Синие линии являются лишь конечными точками и показывают, как взаимодействуют серые линии.
Моя цель: я хотел бы использовать линейное программирование, чтобы равномерно максимизировать размер серых линий, как на картинке. Вы можете себе представить серые линии с пружинами на них, все одинаково выталкивающие наружу. Плохое решение - переместить все синие линии как можно дальше в одну сторону. Обратите внимание, что в этом описании есть некоторая свобода действий, и возможны несколько решений - все, что мне нужно, - это чтобы они были достаточно равномерными, и чтобы одно значение не было максимальным, подавляя все остальное.
Целевая функция, которую я пробовал, просто максимизирует сумму размера строки:
maximize: (B - A) + (C - B) + (C - A) + (D - C) + (E - B) + (E - D) + (F - E) + (F - D) + (F - A)
Для меня ясно, что это не очень хорошее решение, так как условия отменяются, а увеличение одной строки просто уменьшает его в другой на ту же величину, поэтому цель никогда не взвешивается в направлении равномерного распределения максимизации между переменными.
Я также пытался минимизировать расстояние каждой линии от их среднего возможного диапазона. Для линии B - A, среднее значение в его диапазоне (1,3) является 2, Вот цель первого термина:
minimize: |(B - A) - 2| + ...
Чтобы реализовать абсолютное значение, я заменил термин U и добавил дополнительные ограничения:
minimize: U + ...
with: U <= (B - A - 2)
U <= -(B - A - 2)
Это имеет ту же проблему, что и другая цель: разница всегда пропорциональна изменению разницы в другой строке. Я думаю, что это сработало бы, если бы я мог выровнять разницу, но я не могу ввести это в линейный решатель.
Есть ли какая-то объективная функция, которая бы достигла того, что я ищу, или линейный решатель просто не подходит для этого?
Я использую Google OR-Tools, если это поможет.
Вот выписанные ограничения:
1 <= B - A <= 3
0 <= C - B <= 1
1 <= C - A <= 4
9 <= E - B <= 11
7 <= D - C <= 11
0 <= E - D <= 1
3 <= F - E <= 5
3 <= F - D <= 6
15 <= F - A < = 15
1 ответ
Имейте в виду, что ваша самая большая проблема заключается в том, что вы не знаете, что именно вы хотите. Так что я должен был угадать. Иногда просмотр нескольких догадок помогает вам уточнить, что вы хотите, так что это не так уж плохо с вашей стороны, но это усложняет ваш вопрос для формата этого сайта.
Во-первых, я предполагаю, что пружины можно смоделировать как ориентированный ациклический граф. То есть я могу заменить все пружины стрелками, которые указывают вправо. Там никогда не будет стрелка, указывающая справа налево (иначе ваши пружины будут изгибаться по кругу).
Как только это будет сделано, вы можете использовать набор логики, чтобы выяснить идентичность самой левой синей полосы. (Я предполагаю, что есть только один - это оставлено как упражнение, чтобы выяснить, как обобщать.) Затем вы можете закрепить эту полосу в подходящем месте. Все остальные бары будут расположены относительно него. Это ограничение выглядит так:
S[leftmost] = 0
Теперь нам нужны некоторые ограничения.
Каждый край i имеет источник и конечную точку (потому что края направлены). Назовите позицию исходной точки S и положение конечной точки E, Кроме того, край имеет минимальную длину l и максимальная длина L, Поскольку мы фиксируем местоположение самой левой синей панели, связанные с ней пружины определяют интервалы, в которые попадают их конечные точки. Эти конечные точки являются исходными точками для других источников, &c. Таким образом, каждое ребро определяет два ограничения на положение своей конечной точки.
S[i]+l[i] <= E[i]
E[i] <= S+L[i]
Кроме того, обратите внимание, что теперь мы можем сформулировать простую линейную программу:
min 1
s.t. S[leftmost] = 0
S[i]+l[i] <= E[i]
E[i] <= S+L[i]
Если эта программа может быть решена, то есть реальное решение вашей проблемы. То есть длины столбцов не дают взаимно непоследовательного описания того, где должны быть синие столбцы.
Теперь мы хотим "равномерно увеличить размер серых линий", что бы это ни значило.
Минимизация отклонения от средней длины
Вот одна идея. Длина, которую программа выбирает для каждого бара, определяется как E[i]-S[i], Давайте уточним, что эта длина должна быть "близка к" средней длине бара (L[i]+l[i])/2, Таким образом, целевое количество, которое мы хотим минимизировать для каждого бара:
(E[i]-S[i])-(L[i]+l[i])/2
Проблемно, это значение может быть положительным или отрицательным в зависимости от того, (E[i]-S[i])>(L[i]+l[i])/2, Это не хорошо, потому что мы хотим минимизировать отклонение от (L[i]+l[i])/2значение, которое всегда должно быть положительным.
Чтобы справиться, давайте возведем в квадрат значение и затем возьмем квадратный корень, это дает:
sqrt(((E[i]-S[i])-(L[i]+l[i])/2)^2)
Это может показаться неразрешимым, но оставайтесь со мной.
Обратите внимание, что вышесказанное аналогично взятию нормы L2 одноэлементного вектора, поэтому мы можем переписать ее следующим образом:
|(E[i]-S[i])-(L[i]+l[i])/2|_2
Теперь мы можем суммировать отклонения для каждого бара:
|(E[0]-S[0])-(L[0]+l[0])/2|_2 + |(E[1]-S[1])-(L[1]+l[1])/2|_2 + ...
Это дает нам следующую проблему оптимизации:
min |(E[0]-S[0])-(L[0]+l[0])/2|_2 + |(E[1]-S[1])-(L[1]+l[1])/2|_2 + ...
s.t. S[leftmost] = 0
S[i]+l[i] <= E[i]
E[i] <= S+L[i]
Эту проблему нелегко решить в указанной выше форме, но мы можем выполнить простую манипуляцию, введя переменную t
min t[0] + t[1] + ...
s.t. S[leftmost] = 0
S[i]+l[i] <= E[i]
E[i] <= S+L[i]
|(E[i]-S[i])-(L[i]+l[i])/2|_2<=t[i]
Эта проблема точно такая же, как и предыдущая. Итак, что мы получили?
Оптимизация - это игра преобразования задач в стандартные формы. Как только у нас возникнет проблема в стандартной форме, мы сможем встать на плечи гигантов и использовать мощные инструменты для решения наших проблем.
Вышеуказанные манипуляции превратили проблему в проблему конуса второго порядка (SOCP). Оказавшись в этой форме, это может быть решено в значительной степени напрямую.
Код для этого выглядит следующим образом:
#!/usr/bin/env python3
import cvxpy as cp
import networkx as nx
import matplotlib.pyplot as plt
def FindTerminalPoints(springs):
starts = set([x[0] for x in springs.edges()])
ends = set([x[1] for x in springs.edges()])
return list(starts-ends), list(ends-starts)
springs = nx.DiGraph()
springs.add_edge('a', 'b', minlen= 1, maxlen= 3)
springs.add_edge('a', 'c', minlen= 1, maxlen= 4)
springs.add_edge('a', 'f', minlen=15, maxlen=15)
springs.add_edge('b', 'c', minlen= 0, maxlen= 1)
springs.add_edge('b', 'e', minlen= 9, maxlen=11)
springs.add_edge('c', 'd', minlen= 7, maxlen=11)
springs.add_edge('d', 'e', minlen= 0, maxlen= 1)
springs.add_edge('d', 'f', minlen= 3, maxlen= 6)
springs.add_edge('e', 'f', minlen= 3, maxlen= 5)
if not nx.is_directed_acyclic_graph(springs):
raise Exception("Springs must be a directed acyclic graph!")
starts, ends = FindTerminalPoints(springs)
if len(starts)!=1:
raise Exception("One unique start is needed!")
if len(ends)!=1:
raise Exception("One unique end is needed!")
start = starts[0]
end = ends[0]
#At this point we have what is essentially a directed acyclic graph beginning at
#`start` and ending at `end`
#Generate a variable for the position of each blue bar
bluevars = {n: cp.Variable(name=n) for n in springs.nodes()}
dvars = {e: cp.Variable() for e in springs.edges()}
#Anchor the leftmost blue bar to prevent pathological solutions
cons = [bluevars[start]==0]
for s,e in springs.edges():
print("Loading edge {0}-{1}".format(s,e))
sv = bluevars[s]
ev = bluevars[e]
edge = springs[s][e]
cons += [sv+edge['minlen']<=ev]
cons += [ev<=sv+edge['maxlen']]
cons += [cp.norm((ev-sv)-(edge['maxlen']-edge['minlen'])/2,2)<=dvars[(s,e)]]
obj = cp.Minimize(cp.sum(list(dvars.values())))
prob = cp.Problem(obj,cons)
val = prob.solve()
fig, ax = plt.subplots()
for var, val in bluevars.items():
print("{:10} = {:10}".format(var,val.value))
plt.plot([val.value,val.value],[0,3])
plt.show()
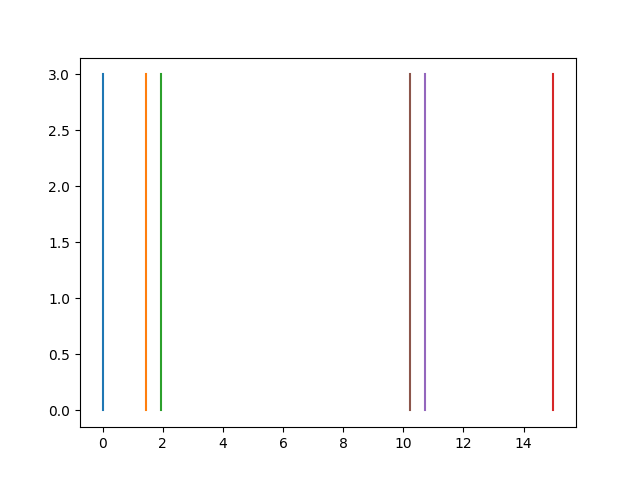
Результаты выглядят так:
Если вы хотите вручную настроить синие полосы, вы можете изменить построенную нами задачу оптимизации, добавив веса w[i],
min w[0]*t[0] + w[1]*t[1] + ...
s.t. S[leftmost] = 0
S[i]+l[i] <= E[i]
E[i] <= S+L[i]
|(E[i]-S[i])-(L[i]+l[i])/2|_2<=t[i]
Чем больше w[i] тем важнее будет то, что рассматриваемая пружина близка к ее средней длине.
Минимизация квадрата расстояния между упорядоченными синими полосами с учетом ограничений
Используя те же стратегии, что и выше, мы можем минимизировать квадратное расстояние между синими столбцами, принимая некоторый известный порядок. Это ведет к:
min t[0] + t[1] + ...
s.t. S[leftmost] = 0
S[i]+l[i] <= E[i]
E[i] <= S+L[i]
|(S[i]-S[i+1])/2|_2<=t[i]
В приведенном ниже коде я сначала нахожу возможные положения синих столбцов, а затем предполагаю, что они отображаются в желаемом порядке. Замена этой эвристики на более точную информацию была бы хорошей идеей.
#!/usr/bin/env python3
import cvxpy as cp
import networkx as nx
import matplotlib.pyplot as plt
def FindTerminalPoints(springs):
starts = set([x[0] for x in springs.edges()])
ends = set([x[1] for x in springs.edges()])
return list(starts-ends), list(ends-starts)
springs = nx.DiGraph()
springs.add_edge('a', 'b', minlen= 1, maxlen= 3)
springs.add_edge('a', 'c', minlen= 1, maxlen= 4)
springs.add_edge('a', 'f', minlen=15, maxlen=15)
springs.add_edge('b', 'c', minlen= 0, maxlen= 1)
springs.add_edge('b', 'e', minlen= 9, maxlen=11)
springs.add_edge('c', 'd', minlen= 7, maxlen=11)
springs.add_edge('d', 'e', minlen= 0, maxlen= 1)
springs.add_edge('d', 'f', minlen= 3, maxlen= 6)
springs.add_edge('e', 'f', minlen= 3, maxlen= 5)
if not nx.is_directed_acyclic_graph(springs):
raise Exception("Springs must be a directed acyclic graph!")
starts, ends = FindTerminalPoints(springs)
if len(starts)!=1:
raise Exception("One unique start is needed!")
if len(ends)!=1:
raise Exception("One unique end is needed!")
start = starts[0]
end = ends[0]
#At this point we have what is essentially a directed acyclic graph beginning at
#`start` and ending at `end`
#Generate a variable for the position of each blue bar
bluevars = {n: cp.Variable(name=n) for n in springs.nodes()}
#Anchor the leftmost blue bar to prevent pathological solutions
cons = [bluevars[start]==0]
#Constraint each blue bar to its range
for s,e in springs.edges():
print("Loading edge {0}-{1}".format(s,e))
sv = bluevars[s]
ev = bluevars[e]
edge = springs[s][e]
cons += [sv+edge['minlen']<=ev]
cons += [ev<=sv+edge['maxlen']]
#Find feasible locations for the blue bars. This is a heuristic for getting a
#sorted order for the bars
obj = cp.Minimize(1)
prob = cp.Problem(obj,cons)
prob.solve()
#Now that we have a sorted order, we modify the objective to minimize the
#squared distance between the ordered bars
bar_locs = list(bluevars.values())
bar_locs.sort(key=lambda x: x.value)
dvars = [cp.Variable() for n in range(len(springs.nodes())-1)]
for i in range(len(bar_locs)-1):
cons += [cp.norm(bar_locs[i]-bar_locs[i+1],2)<=dvars[i]]
obj = cp.Minimize(cp.sum(dvars))
prob = cp.Problem(obj,cons)
val = prob.solve()
fig, ax = plt.subplots()
for var, val in bluevars.items():
print("{:10} = {:10}".format(var,val.value))
plt.plot([val.value,val.value],[0,3])
plt.show()
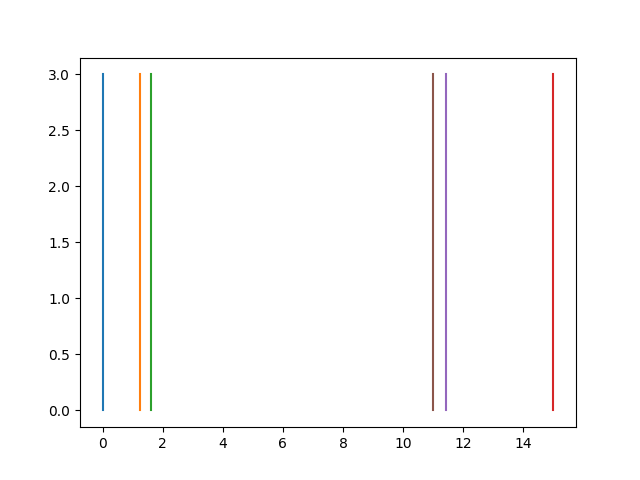
Это выглядит так:
Минимизация квадрата расстояния между всеми синими полосами с учетом ограничений
Мы также могли бы попытаться минимизировать все попарно возведенные в квадрат расстояния между синими полосами. На мой взгляд, это дает лучший результат.
min t[i,j] + ... for all i,j
s.t. S[leftmost] = 0
S[i]+l[i] <= E[i] for all i
E[i] <= S+L[i] for all i
|(S[i]-S[j])/2|_2 <= t[i,j] for all i,j
Это будет выглядеть так:
#!/usr/bin/env python3
import cvxpy as cp
import networkx as nx
import matplotlib.pyplot as plt
import itertools
def FindTerminalPoints(springs):
starts = set([x[0] for x in springs.edges()])
ends = set([x[1] for x in springs.edges()])
return list(starts-ends), list(ends-starts)
springs = nx.DiGraph()
springs.add_edge('a', 'b', minlen= 1, maxlen= 3)
springs.add_edge('a', 'c', minlen= 1, maxlen= 4)
springs.add_edge('a', 'f', minlen=15, maxlen=15)
springs.add_edge('b', 'c', minlen= 0, maxlen= 1)
springs.add_edge('b', 'e', minlen= 9, maxlen=11)
springs.add_edge('c', 'd', minlen= 7, maxlen=11)
springs.add_edge('d', 'e', minlen= 0, maxlen= 1)
springs.add_edge('d', 'f', minlen= 3, maxlen= 6)
springs.add_edge('e', 'f', minlen= 3, maxlen= 5)
if not nx.is_directed_acyclic_graph(springs):
raise Exception("Springs must be a directed acyclic graph!")
starts, ends = FindTerminalPoints(springs)
if len(starts)!=1:
raise Exception("One unique start is needed!")
if len(ends)!=1:
raise Exception("One unique end is needed!")
start = starts[0]
end = ends[0]
#At this point we have what is essentially a directed acyclic graph beginning at
#`start` and ending at `end`
#Generate a variable for the position of each blue bar
bluevars = {n: cp.Variable(name=n) for n in springs.nodes()}
#Anchor the leftmost blue bar to prevent pathological solutions
cons = [bluevars[start]==0]
#Constraint each blue bar to its range
for s,e in springs.edges():
print("Loading edge {0}-{1}".format(s,e))
sv = bluevars[s]
ev = bluevars[e]
edge = springs[s][e]
cons += [sv+edge['minlen']<=ev]
cons += [ev<=sv+edge['maxlen']]
dist_combos = list(itertools.combinations(springs.nodes(), 2))
dvars = {(na,nb):cp.Variable() for na,nb in dist_combos}
distcons = []
for na,nb in dist_combos:
distcons += [cp.norm(bluevars[na]-bluevars[nb],2)<=dvars[(na,nb)]]
cons += distcons
#Find feasible locations for the blue bars. This is a heuristic for getting a
#sorted order for the bars
obj = cp.Minimize(cp.sum(list(dvars.values())))
prob = cp.Problem(obj,cons)
val = prob.solve()
fig, ax = plt.subplots()
for var, val in bluevars.items():
print("{:10} = {:10}".format(var,val.value))
plt.plot([val.value,val.value],[0,3])
plt.show()
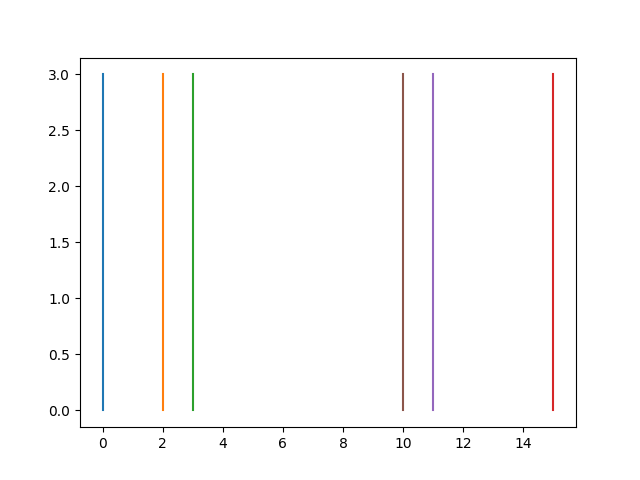
Это выглядит так:
