Побитовое вычисление последовательности LFSR с использованием нотации в стиле CRC
Мой вопрос связан с наблюдением, что мы можем использовать регистр сдвига с линейной обратной связью для проверки CRC. Алгебраически это обычно имеет форму;
S (x) = M (x) * x ^ k% G(x) (дает остаток для G(x) порядка k)
Реализация этого показана в этом вопросе(и все регистры инициализируются нулем), и математическое побитовое вычисление деления XOR показано в этом вопросе здесь.
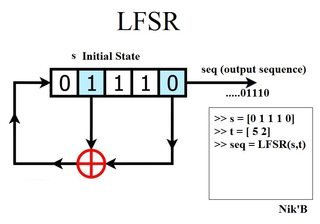
Я понимаю оба из них - однако, я также знаю, что другим распространенным способом использования LFSR является отсутствие входных данных, а вместо этого предварительная загрузка регистров с ненулевыми значениями и запуск (с нулевым значением в качестве входных данных) для формирования последовательности псевдослучайные числа. Это показано на рисунке ниже
Мой вопрос так же, как CRC может быть представлен как деление по модулю-2 как поразрядно, так и алгебраически, можем ли мы сделать то же самое для генератора последовательности LFSR, учитывая полином генератора и начальные значения? И если так, пример был бы великолепен!
Большое спасибо, не стесняйтесь поправлять меня, если я исказил или неправильно понял концепцию!