Понимание двух разных способов реализации генерации CRC с LFSR

Question

Существует два способа реализации генерации CRC с помощью регистров сдвига с линейной обратной связью (LFSR), как показано на этом рисунке. 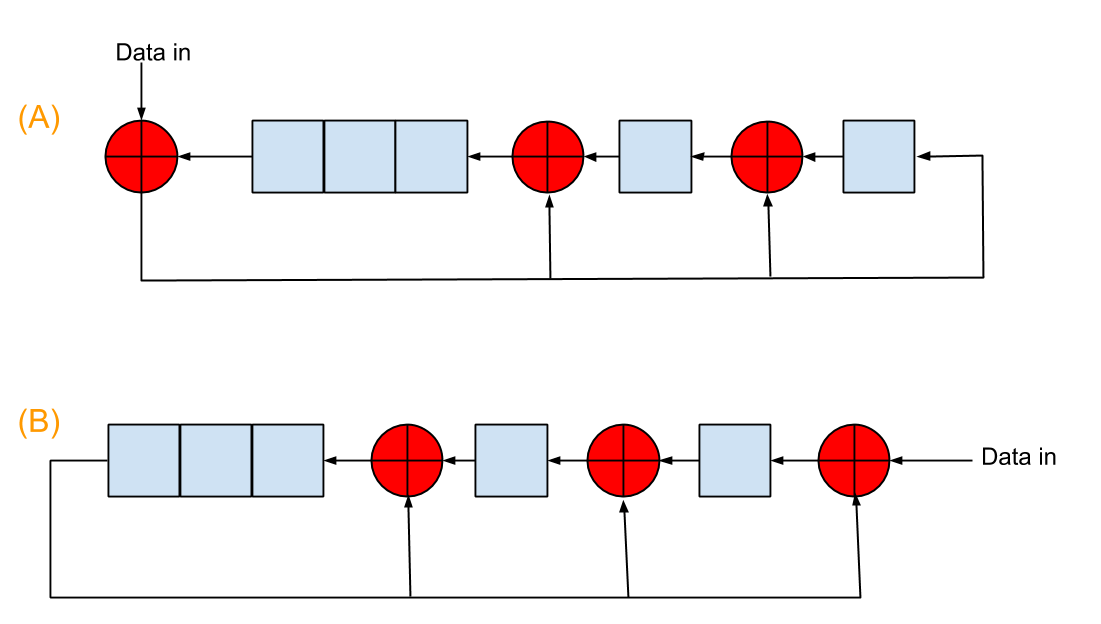, Коэффициенты порождающего полинома на этой картинке равны 100111, а красные кружки "+" являются исключающими или операторами. Значения регистра инициализации равны 00000 для обоих.

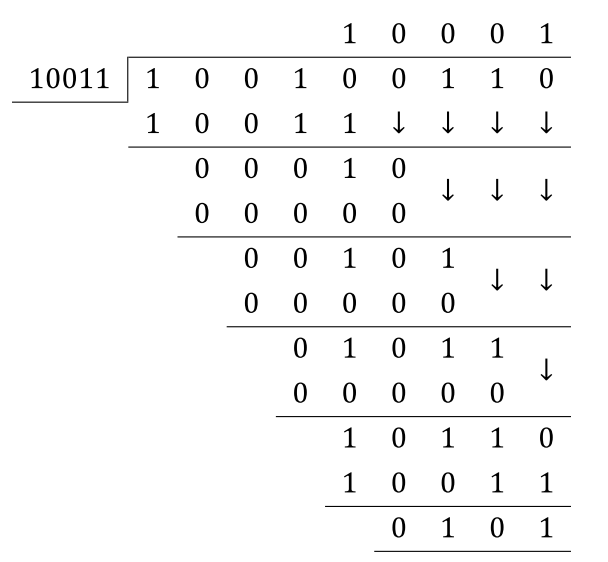
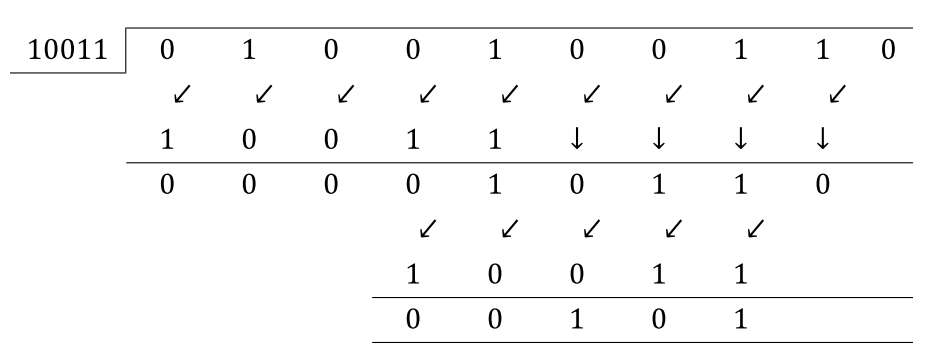
Например, если поток битов входных данных равен 10010011, и A, и B дадут контрольную сумму CRC, равную 1010. Разница в том, что A заканчивается с 8 сменами, а B с 8+5=13 сдвигами из-за 5 нулей, добавленных к входу. данные. Я могу понять B очень легко, так как он близко имитирует деление по модулю-2. Тем не менее, я не могу математически понять, как А может дать тот же результат с 5 меньшими сменами. Я слышал, что люди говорили, что воспользовались предварительно добавляемыми нулями, но я не понял. Кто-нибудь может мне это объяснить? Спасибо!

Answer 1

Вот мое быстрое понимание.

Пусть M(x) будет входным сообщением порядка m (т.е. имеет m+1 бит), а G(x) будет полиномом CRC порядка n. Результат CRC для такого сообщения

C (x) = (M(x) * xⁿ)% G(x)

Это то, что реализует схема B. Требуются дополнительные 5 циклов из-за операции xⁿ.

Вместо того, чтобы следовать этому подходу, схема А пытается сделать что-то умнее. Это пытается решить вопрос

Если C (x) является CRC для M(x), то каким будет CRC для сообщения {M(x), D}

где D - новый бит Таким образом, он пытается решить один бит за раз вместо всего сообщения, как в случае схемы b. Следовательно, схема 8 займет 8 циклов для 8-битного сообщения.

Теперь, когда вы уже понимаете, почему схема B выглядит так, как она делает, давайте посмотрим на схему A. Математика, специально для вашего случая, для эффекта добавления бита D к сообщению M(x) на CRC, как показано ниже

Пусть текущий CRC C (x) будет {c4, c3, c2, c1, c0} и новый бит, который сдвинут в, будет D
NewCRC = {M(x), D} * x⁵)% G(x) = (({M(x), 0} * x⁵)% G(x)) XOR ((D * x⁵)% G (Икс))
который является ({c3, c2, c1, c0, 0} XOR {0, 0, c4, c4, c4}) XOR ({0, 0, D, D, D})
который является {c3, c2, c1^c4^D, c0^c4^D, c4^D}

т.е. схема LFSR A.

Answer 2

Вы можете сказать, что архитектура (A) реализует деление по модулю путем выравнивания MSB полинома с MSB сообщения, поэтому она реализует что-то вроде следующего (в моем примере на самом деле у меня есть еще один полином crc):

Но в архитектуре (B) вы можете сказать, что мы пытаемся предсказать MSB сообщения, поэтому мы выравниваем MSB полинома CRC с MSB-1 сообщения, что-то вроде следующего:

Я могу порекомендовать подробности об этой операции в этом руководстве.