Mathematica: 3D проволочные каркасы
Поддерживает ли Mathematica удаление скрытых линий для изображений каркаса? Если это не так, кто-нибудь здесь когда-нибудь сталкивался с этим? Начнем с этого:
Plot3D[Sin[x+y^2], {x, -3, 3}, {y, -2, 2}, Boxed -> False]
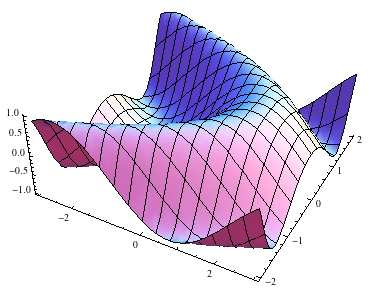
Для создания каркаса мы можем сделать:
Plot3D[Sin[x+y^2], {x, -3, 3}, {y, -2, 2}, Boxed -> False, PlotStyle -> None]
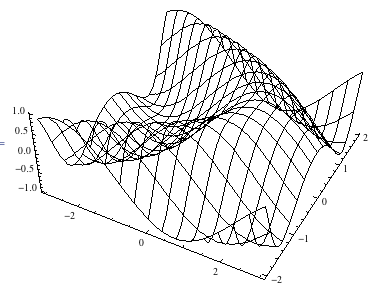
Одна вещь, которую мы можем сделать, чтобы добиться эффекта, это покрасить все поверхности в белый цвет. Это, однако, нежелательно. Причина в том, что если мы экспортируем эту модель каркаса скрытой линии в pdf, у нас будут все те белые полигоны, которые Mathematica использует для визуализации изображения. Я хочу быть в состоянии получить каркас с удалением скрытых линий в формате PDF и / или EPS.
ОБНОВИТЬ:
Я разместил решение этой проблемы. Проблема в том, что код работает очень медленно. В своем текущем состоянии он не может создать каркас для изображения в этом вопросе. Не стесняйтесь играть с моим кодом. Я добавил ссылку на него в конце своего поста. Вы также можете найти код в этой ссылке
2 ответа
Здесь я представляю решение. Сначала я покажу, как использовать функцию, которая генерирует каркас, затем я подробно объясню остальные функции, составляющие алгоритм.
wireFrame
wireFrame[g_] := Module[{figInfo, opt, pts},
{figInfo, opt} = G3ToG2Info[g];
pts = getHiddenLines[figInfo];
Graphics[Map[setPoints[#] &, getFrame[figInfo, pts]], opt]
]
Ввод этой функции Graphics3D объект желательно без осей.
fig = ListPlot3D[
{{0, -1, 0}, {0, 1, 0}, {-1, 0, 1}, {1, 0, 1}, {-1, 1, 1}},
Mesh -> {10, 10},
Boxed -> False,
Axes -> False,
ViewPoint -> {2, -2, 1},
ViewVertical -> {0, 0, 1},
MeshStyle -> Directive[RGBColor[0, 0.5, 0, 0.5]],
BoundaryStyle -> Directive[RGBColor[1, 0.5, 0, 0.5]]
]

Теперь мы применяем функцию wireFrame,
wireFrame[fig]
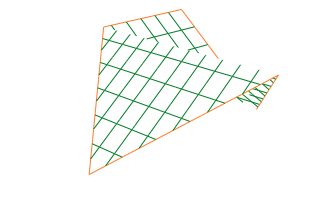
Как вы видете wireFrame Получил большинство линий и его цветов. Есть зеленая линия, которая не была включена в каркас. Скорее всего это связано с моими настройками порога.
Прежде чем приступить к объяснению деталей функций G3ToG2Info, getHiddenLines, getFrame а также setPoints Я покажу вам, почему каркасные рамки с удалением скрытых линий могут быть полезны.
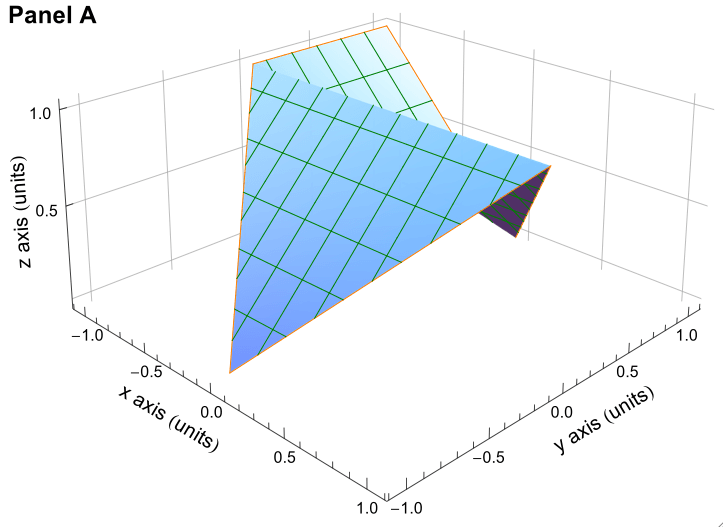
Изображение, показанное выше, представляет собой скриншот файла PDF, созданного с использованием метода, описанного в растрах в трехмерной графике, в сочетании с каркасным каркасом, сгенерированным здесь. Это может быть выгодно различными способами. Нет необходимости хранить информацию для треугольников, чтобы показать красочную поверхность. Вместо этого мы показываем растровое изображение поверхности. Все линии очень плавные, за исключением того, что границы растрового графика не покрыты линиями. У нас также есть уменьшение размера файла. В этом случае размер файла PDF уменьшился с 1,9 МБ до 78 КБ с использованием комбинации растрового изображения и каркасной структуры. Отображение в программе просмотра PDF занимает меньше времени, а качество изображения отличное.
Mathematica неплохо справляется с экспортом 3D-изображений в PDF-файлы. Когда мы импортируем файлы PDF, мы получаем объект Graphics, состоящий из отрезков и треугольников. В некоторых случаях эти объекты перекрываются, и поэтому у нас есть скрытые линии. Чтобы сделать каркасную модель без поверхностей, сначала нужно удалить это перекрытие, а затем удалить многоугольники. Я начну с описания того, как получить информацию из изображения Graphics3D.
G3ToG2Info
getPoints[obj_] := Switch[Head[obj],
Polygon, obj[[1]],
JoinedCurve, obj[[2]][[1]],
RGBColor, {Table[obj[[i]], {i, 1, 3}]}
];
setPoints[obj_] := Switch[Length@obj,
3, Polygon[obj],
2, Line[obj],
1, RGBColor[obj[[1]]]
];
G3ToG2Info[g_] := Module[{obj, opt},
obj = ImportString[ExportString[g, "PDF", Background -> None], "PDF"][[1]];
opt = Options[obj];
obj = Flatten[First[obj /. Style[expr_, opts___] :> {opts, expr}], 2];
obj = Cases[obj, _Polygon | _JoinedCurve | _RGBColor, Infinity];
obj = Map[getPoints[#] &, obj];
{obj, opt}
]
Этот код для Mathematica 8 в версии 7 вы бы заменили JoinedCurve в функции getPoints от Line, Функция getPoints предполагает, что вы даете примитив Graphics объект. Он увидит, какой тип объекта он получает, а затем извлечет из него нужную ему информацию. Если это многоугольник, он получает список из 3 точек, для линии он получает список из 2 точек, а если это цвет, то он получает список из одного списка, содержащий 3 точки. Это было сделано так, чтобы сохранить согласованность со списками.
Функция setPoints делает обратное getPoints, Вы вводите список точек, и он определяет, должен ли он возвращать многоугольник, линию или цвет.
Для получения списка треугольников, линий и цветов мы используем G3ToG2Info, Эта функция будет использовать ExportString а также ImportString чтобы получить Graphics объект из Graphics3D версия. Эта информация хранится в obj, Нам нужно провести некоторую очистку, сначала мы получим варианты obj, Эта часть необходима, потому что она может содержать PlotRange изображения. Тогда мы получим все Polygon, JoinedCurve а также RGBColor объекты, как описано в получении графических примитивов и директив. Наконец мы применяем функцию getPoints на всех этих объектах, чтобы получить список треугольников, линий и цветов. Эта часть охватывает линию {figInfo, opt} = G3ToG2Info[g],
getHiddenLines
Мы хотим знать, какая часть строки не будет отображаться. Для этого нам нужно знать точку пересечения двух отрезков. Алгоритм, который я использую, чтобы найти пересечение, можно найти здесь.
lineInt[L_, M_, EPS_: 10^-6] := Module[
{x21, y21, x43, y43, x13, y13, numL, numM, den},
{x21, y21} = L[[2]] - L[[1]];
{x43, y43} = M[[2]] - M[[1]];
{x13, y13} = L[[1]] - M[[1]];
den = y43*x21 - x43*y21;
If[den*den < EPS, Return[-Infinity]];
numL = (x43*y13 - y43*x13)/den;
numM = (x21*y13 - y21*x13)/den;
If[numM < 0 || numM > 1, Return[-Infinity], Return[numL]];
]
lineInt предполагает, что линия L а также M не совпадают. Он вернется -Infinity если линии параллельны или если линия содержит сегмент L не пересекает отрезок M, Если строка, содержащая L пересекает отрезок M тогда он возвращает скаляр. Предположим, этот скаляр uто точка пересечения L[[1]] + u (L[[2]]-L[[1]]), Обратите внимание, что это совершенно нормально для u быть любым реальным числом. Вы можете поиграть с этой функцией манипулирования, чтобы проверить, как lineInt работает.
Manipulate[
Grid[{{
Graphics[{
Line[{p1, p2}, VertexColors -> {Red, Red}],
Line[{p3, p4}]
},
PlotRange -> 3, Axes -> True],
lineInt[{p1, p2}, {p3, p4}]
}}],
{{p1, {-1, 1}}, Locator, Appearance -> "L1"},
{{p2, {2, 1}}, Locator, Appearance -> "L2"},
{{p3, {1, -1}}, Locator, Appearance -> "M1"},
{{p4, {1, 2}}, Locator, Appearance -> "M2"}
]
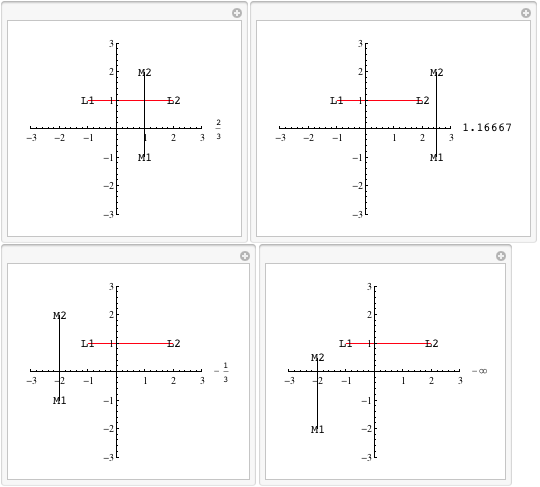
Теперь, когда мы знаем, как далеко мы должны путешествовать от L[[1]] на отрезок M мы можем узнать, какая часть отрезка прямой находится в треугольнике.
lineInTri[L_, T_] := Module[{res},
If[Length@DeleteDuplicates[Flatten[{T, L}, 1], SquaredEuclideanDistance[#1, #2] < 10^-6 &] == 3, Return[{}]];
res = Sort[Map[lineInt[L, #] &, {{T[[1]], T[[2]]}, {T[[2]], T[[3]]}, {T[[3]], T[[1]]} }]];
If[res[[3]] == Infinity || res == {-Infinity, -Infinity, -Infinity}, Return[{}]];
res = DeleteDuplicates[Cases[res, _Real | _Integer | _Rational], Chop[#1 - #2] == 0 &];
If[Length@res == 1, Return[{}]];
If[(Chop[res[[1]]] == 0 && res[[2]] > 1) || (Chop[res[[2]] - 1] == 0 && res[[1]] < 0), Return[{0, 1}]];
If[(Chop[res[[2]]] == 0 && res[[1]] < 0) || (Chop[res[[1]] - 1] == 0 && res[[2]] > 1), Return[{}]];
res = {Max[res[[1]], 0], Min[res[[2]], 1]};
If[res[[1]] > 1 || res[[1]] < 0 || res[[2]] > 1 || res[[2]] < 0, Return[{}], Return[res]];
]
Эта функция возвращает часть строки L это должно быть удалено. Например, если он возвращает {.5, 1} это означает, что вы удалите 50 процентов линии, начиная с половины сегмента и заканчивая конечной точкой сегмента. Если L = {A, B} и функция возвращает {u, v} тогда это означает, что отрезок {A+(B-A)u, A+(B-A)v} это отрезок линии, который содержится в треугольнике T,
При реализации lineInTri Вы должны быть осторожны, что линия L не является одним из краев T, если это так, то линия не лежит внутри треугольника. Вот где ошибки округления могут быть плохими. Когда Mathematica экспортирует изображение, иногда линия лежит на краю треугольника, но эти координаты отличаются в некоторой степени. Мы должны решить, насколько близко линия лежит на краю, в противном случае функция увидит, что линия почти полностью лежит внутри треугольника. Это причина первой строки в функции. Чтобы увидеть, лежит ли линия на краю треугольника, мы можем перечислить все точки треугольника и линии и удалить все дубликаты. Вам необходимо указать, что такое дубликат в этом случае. В конце концов, если мы получим список из 3 точек, это означает, что линия лежит на ребре. Следующая часть немного сложнее. То, что мы делаем, это проверка на пересечение линии L с каждым краем треугольника T и сохраните результаты в списке. Затем мы сортируем список и выясняем, какая часть линии, если таковая имеется, лежит в треугольнике. Попробуйте разобраться в этом, поиграв с этим, в некоторые из тестов входит проверка, является ли конечная точка линии вершиной треугольника, находится ли линия полностью внутри треугольника, частично внутри или полностью снаружи.
Manipulate[
Grid[{{
Graphics[{
RGBColor[0, .5, 0, .5], Polygon[{p3, p4, p5}],
Line[{p1, p2}, VertexColors -> {Red, Red}]
},
PlotRange -> 3, Axes -> True],
lineInTri[{p1, p2}, {p3, p4, p5}]
}}],
{{p1, {-1, -2}}, Locator, Appearance -> "L1"},
{{p2, {0, 0}}, Locator, Appearance -> "L2"},
{{p3, {-2, -2}}, Locator, Appearance -> "T1"},
{{p4, {2, -2}}, Locator, Appearance -> "T2"},
{{p5, {-1, 1}}, Locator, Appearance -> "T3"}
]
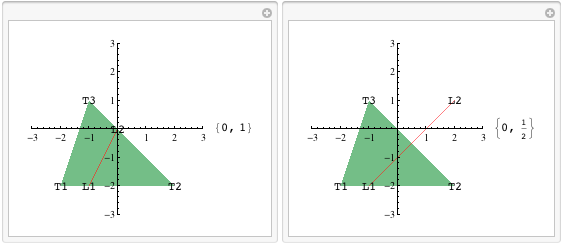
lineInTri будет использоваться, чтобы увидеть, какая часть линии не будет проведена. Эта линия, скорее всего, будет покрыта множеством треугольников. По этой причине нам нужно вести список всех частей каждой линии, которые не будут нарисованы. Эти списки не будут иметь порядок. Все, что мы знаем, это то, что эти списки являются одномерными сегментами. Каждый состоит из чисел в [0,1] интервал. Я не знаю о функции объединения для одномерных сегментов, так что вот моя реализация.
union[obj_] := Module[{p, tmp, dummy, newp, EPS = 10^-3},
p = Sort[obj];
tmp = p[[1]];
If[tmp[[1]] < EPS, tmp[[1]] = 0];
{dummy, newp} = Reap[
Do[
If[(p[[i, 1]] - tmp[[2]]) > EPS && (tmp[[2]] - tmp[[1]]) > EPS,
Sow[tmp]; tmp = p[[i]],
tmp[[2]] = Max[p[[i, 2]], tmp[[2]]]
];
, {i, 2, Length@p}
];
If[1 - tmp[[2]] < EPS, tmp[[2]] = 1];
If[(tmp[[2]] - tmp[[1]]) > EPS, Sow[tmp]];
];
If[Length@newp == 0, {}, newp[[1]]]
]
Эта функция была бы короче, но здесь я включил некоторые операторы if, чтобы проверить, близко ли число к нулю или единице. Если один номер EPS кроме нуля, тогда мы делаем это число ноль, то же самое относится и к одному. Еще один аспект, который я здесь рассматриваю, заключается в том, что если отображается относительно небольшая часть сегмента, то, скорее всего, ее необходимо удалить. Например, если у нас есть {{0,.5}, {.500000000001}} это означает, что нам нужно нарисовать {{.5, .500000000001}}, Но этот сегмент очень мал, чтобы его можно было заметить, особенно в большом отрезке, поскольку все мы знаем, что эти два числа одинаковы. Все это необходимо учитывать при реализации union,
Теперь мы готовы увидеть, что нужно удалить из отрезка. Далее требуется список объектов, созданных из G3ToG2Info, объект из этого списка и индекса.
getSections[L_, obj_, start_ ] := Module[{dummy, p, seg},
{dummy, p} = Reap[
Do[
If[Length@obj[[i]] == 3,
seg = lineInTri[L, obj[[i]]];
If[Length@seg != 0, Sow[seg]];
]
, {i, start, Length@obj}
]
];
If[Length@p == 0, Return[{}], Return[union[First@p]]];
]
getSections возвращает список, содержащий части, которые необходимо удалить из L, Мы знаем это obj это список треугольников, линий и цветов, мы знаем, что объекты в списке с более высоким индексом будут нарисованы поверх объектов с более низким индексом. По этой причине нам нужен индекс start, Это индекс, в котором мы начнем искать треугольники obj, Как только мы найдем треугольник, мы получим часть сегмента, которая лежит в треугольнике, используя функцию lineInTri, В конце мы получим список разделов, которые мы можем объединить, используя union,
Наконец мы добрались до getHiddenLines, Все, что для этого требуется, - это посмотреть на каждый объект в списке, возвращаемом G3ToG2Info и применить функцию getSections, getHiddenLines вернет список списков. Каждый элемент представляет собой список разделов, которые необходимо удалить.
getHiddenLines[obj_] := Module[{pts},
pts = Table[{}, {Length@obj}];
Do[
If[Length@obj[[j]] == 2,
pts[[j]] = getSections[obj[[j]], obj, j + 1]
];
, {j, Length@obj}
];
Return[pts];
]
getFrame
Если вам удалось понять концепции здесь, я уверен, что вы знаете, что будет сделано дальше. Если у нас есть список треугольников, линий и цветов и участков линий, которые необходимо удалить, нам нужно нарисовать только те цвета и участки линий, которые видны. Сначала мы делаем complement функция, это скажет нам, что именно рисовать.
complement[obj_] := Module[{dummy, p},
{dummy, p} = Reap[
If[obj[[1, 1]] != 0, Sow[{0, obj[[1, 1]]}]];
Do[
Sow[{obj[[i - 1, 2]], obj[[i, 1]]}]
, {i, 2, Length@obj}
];
If[obj[[-1, 2]] != 1, Sow[{obj[[-1, 2]], 1}]];
];
If[Length@p == 0, {}, Flatten@ First@p]
]
Теперь getFrame функция
getFrame[obj_, pts_] := Module[{dummy, lines, L, u, d},
{dummy, lines} = Reap[
Do[
L = obj[[i]];
If[Length@L == 2,
If[Length@pts[[i]] == 0, Sow[L]; Continue[]];
u = complement[pts[[i]]];
If[Length@u > 0,
Do[
d = L[[2]] - L[[1]];
Sow[{L[[1]] + u[[j - 1]] d, L[[1]] + u[[j]] d}]
, {j, 2, Length@u, 2 }]
];
];
If[Length@L == 1, Sow[L]];
, {i, Length@obj}]
];
First@lines
]
Заключительные слова
Я несколько доволен результатами алгоритма. Что мне не нравится, так это скорость исполнения. Я написал это так же, как в C/C++/java, используя циклы. Я старался изо всех сил, чтобы использовать Reap а также Sow создавать растущие списки вместо использования функции Append, Независимо от всего этого мне все равно приходилось использовать петли. Следует отметить, что размещенное здесь изображение каркасной рамки заняло 63 секунды. Я попытался сделать каркас для изображения в вопросе, но этот 3D-объект содержит около 32000 объектов. Потребовалось около 13 секунд, чтобы вычислить части, которые должны отображаться для строки. Если мы предположим, что у нас есть 32000 строк, и для всех вычислений потребуется 13 секунд, что займет около 116 часов вычислительного времени.
Я уверен, что это время можно сократить, если мы используем функцию Compile на всех подпрограммах и, возможно, найти способ не использовать Do петли. Могу ли я получить помощь здесь Переполнение стека?
Для вашего удобства я загрузил код в Интернет. Вы можете найти это здесь. Если вы сможете применить измененную версию этого кода к сюжету в вопросе и показать каркас, я отмечу ваше решение как ответ на этот пост.
Бест, Мануэль Лопес
Это не правильно, но несколько интересно:
Plot3D[Sin[x + y^2], {x, -3, 3}, {y, -2, 2}, Boxed -> False,
PlotStyle -> {EdgeForm[None], FaceForm[Red, None]}, Mesh -> False]
С FaceForm None полигон не отображается. Я не уверен, что есть способ сделать это с помощью линий сетки.