Mathematica: растры в 3D графике
Есть моменты, когда экспорт в PDF-изображение просто хлопотно. Если данные, которые вы строите, содержат много точек, тогда ваша фигура будет большого размера, и просмотрщик PDF по вашему выбору будет тратить большую часть своего времени на рендеринг этого высококачественного изображения. Таким образом, мы можем экспортировать это изображение в формате JPEG, PNG или TIFF. Изображение будет хорошо с определенного вида, но при увеличении оно будет выглядеть искаженным. В некоторой степени это хорошо для фигуры, которую мы строим, но если ваше изображение содержит текст, то этот текст будет выглядеть пиксельным.
Чтобы попытаться получить лучшее из обоих миров, мы можем разделить эту фигуру на две части: оси с метками и трехмерное изображение. Таким образом, оси можно экспортировать в формате PDF или EPS, а 3D-фигуры - в растр. Хотелось бы, чтобы я знал, как позже объединить их в Mathematica, поэтому на данный момент мы можем использовать редактор векторной графики, такой как Inkscape или Illustrator, для их объединения.
Мне удалось добиться этого для сюжета, который я сделал в публикации, но это побудило меня создать подпрограммы в Mathematica для автоматизации этого процесса. Вот что у меня так далеко:
SetDirectory[NotebookDirectory[]];
SetOptions[$FrontEnd, PrintingStyleEnvironment -> "Working"];
Мне нравится запускать записную книжку, устанавливая рабочий каталог в каталог записной книжки. Так как я хочу, чтобы мои изображения имели размер, который я указал, я установил рабочую среду стиля печати, проверьте это для получения дополнительной информации.
in = 72;
G3D = Graphics3D[
AlignmentPoint -> Center,
AspectRatio -> 0.925,
Axes -> {True, True, True},
AxesEdge -> {{-1, -1}, {1, -1}, {-1, -1}},
AxesStyle -> Directive[10, Black],
BaseStyle -> {FontFamily -> "Arial", FontSize -> 12},
Boxed -> False,
BoxRatios -> {3, 3, 1},
LabelStyle -> Directive[Black],
ImagePadding -> All,
ImageSize -> 5 in,
PlotRange -> All,
PlotRangePadding -> None,
TicksStyle -> Directive[10],
ViewPoint -> {2, -2, 2},
ViewVertical -> {0, 0, 1}
]
Здесь мы устанавливаем вид сюжета, который мы хотим сделать. Теперь давайте создадим наш сюжет.
g = Show[
Plot3D[Sin[x y], {x, 0, Pi}, {y, 0, Pi},
Mesh -> None,
AxesLabel -> {"x", "y", "z"}
],
Options[G3D]
]
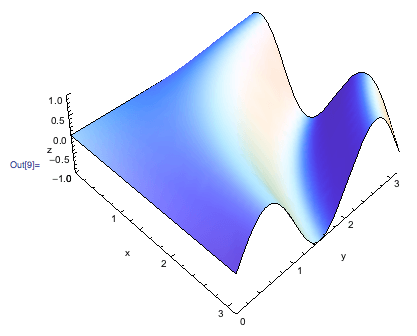
Теперь нам нужно найти способ разделения. Давайте начнем с рисования осей.
axes = Graphics3D[{}, AbsoluteOptions[g]]
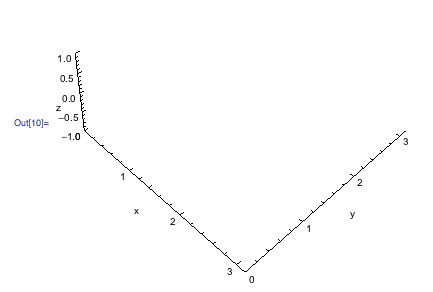
fig = Show[g,
AxesStyle -> Directive[Opacity[0]],
FaceGrids -> {{-1, 0, 0}, {0, 1, 0}}
]
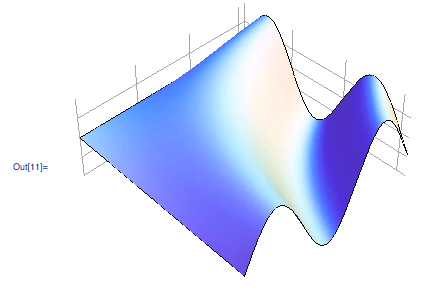
Я включил грани сетки, чтобы мы могли сопоставить фигуру с осью в процессе редактирования. Теперь мы экспортируем оба изображения.
Export["Axes.pdf", axes];
Export["Fig.pdf", Rasterize[fig, ImageResolution -> 300]];
Вы получите два файла PDF, которые вы можете отредактировать и объединить в PDF или EPS. Хотелось бы, чтобы все было так просто, но это не так. Если вы действительно сделали это, вы получите это:
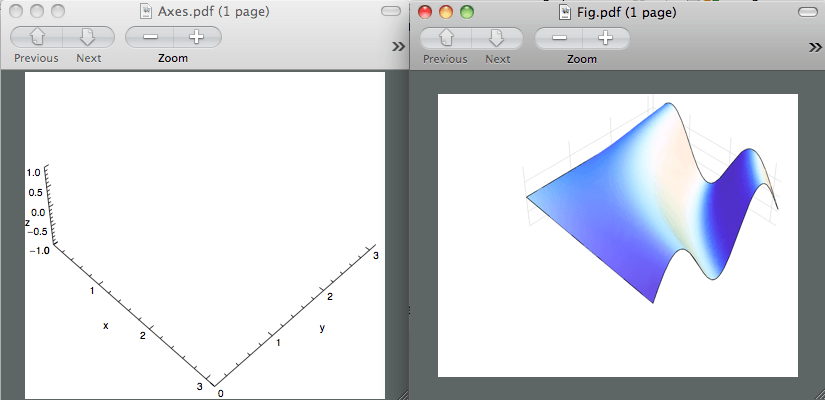
Две фигуры разных размеров. Я знаю, что файл axes.pdf правильный, потому что, когда я открываю его в Inkspace, размер фигуры составляет 5 дюймов, как я ранее указал.
Я упоминал ранее, что мне удалось получить это на одном из моих участков. Я буду чистить файл и менять графики, чтобы сделать его более доступным для всех, кто хочет убедиться, что это действительно так. В любом случае, кто-нибудь знает, почему я не могу получить два файла PDF одинакового размера? Также имейте в виду, что мы хотим получить симпатичный сюжет для растеризованной фигуры. Спасибо за ваше время.
PS. В качестве бонуса, можем ли мы избежать редактирования поста и просто объединить две цифры в mathematica? Растеризованная версия и версия с векторной графикой.
РЕДАКТИРОВАТЬ:
Спасибо rcollyer за его комментарий. Я публикую результаты своего комментария.
Стоит отметить, что когда мы экспортируем оси, нам нужно установить Background в None так что мы можем иметь прозрачную картину.
Export["Axes.pdf", axes, Background -> None];
Export["Fig.pdf", Rasterize[fig, ImageResolution -> 300]];
a = Import["Axes.pdf"];
b = Import["Fig.pdf"];
Show[b, a]
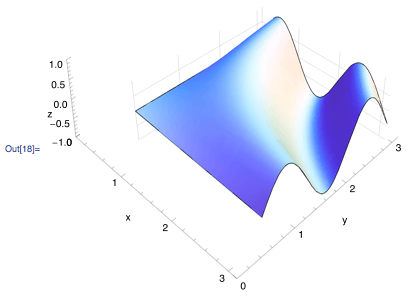
И тогда экспорт рисунка дает желаемый эффект
Export["FinalFig.pdf", Show[b, a]]
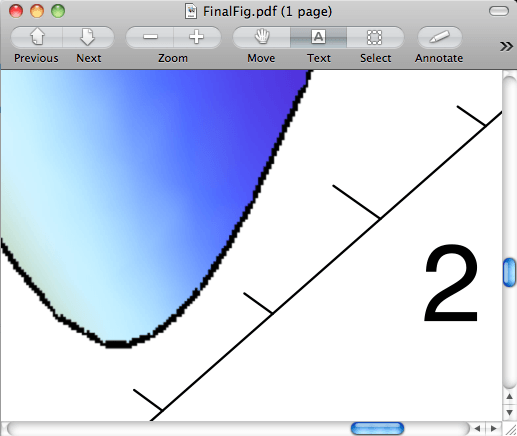
Оси сохраняют прекрасные компоненты векторной графики, в то время как рисунок теперь является растеризованной версией того, что мы нарисовали. Но главный вопрос все еще остается. Как сделать так, чтобы две цифры совпадали?
ОБНОВИТЬ:
На мой вопрос ответил Алексей Попков. Я хотел бы поблагодарить его за то, что он нашел время, чтобы разобраться в моей проблеме. Следующий код является примером для тех, кто хочет использовать технику, которую я упоминал ранее. Пожалуйста, смотрите ответ Алексея Попкова за полезные комментарии в его коде. Ему удалось заставить его работать в Mathematica 7, а в Mathematica 8 он работает еще лучше. Вот результат:
SetDirectory[NotebookDirectory[]];
SetOptions[$FrontEnd, PrintingStyleEnvironment -> "Working"];
$HistoryLength = 0;
in = 72;
G3D = Graphics3D[
AlignmentPoint -> Center, AspectRatio -> 0.925, Axes -> {True, True, True},
AxesEdge -> {{-1, -1}, {1, -1}, {-1, -1}}, AxesStyle -> Directive[10, Black],
BaseStyle -> {FontFamily -> "Arial", FontSize -> 12}, Boxed -> False,
BoxRatios -> {3, 3, 1}, LabelStyle -> Directive[Black], ImagePadding -> 40,
ImageSize -> 5 in, PlotRange -> All, PlotRangePadding -> 0,
TicksStyle -> Directive[10], ViewPoint -> {2, -2, 2}, ViewVertical -> {0, 0, 1}
];
axesLabels = Graphics3D[{
Text[Style["x axis (units)", Black, 12], Scaled[{.5, -.1, 0}], {0, 0}, {1, -.9}],
Text[Style["y axis (units)", Black, 12], Scaled[{1.1, .5, 0}], {0, 0}, {1, .9}],
Text[Style["z axis (units)", Black, 12], Scaled[{0, -.15, .7}], {0, 0}, {-.1, 1.5}]
}];
fig = Show[
Plot3D[Sin[x y], {x, 0, Pi}, {y, 0, Pi}, Mesh -> None],
ImagePadding -> {{40, 0}, {15, 0}}, Options[G3D]
];
axes = Show[
Graphics3D[{}, FaceGrids -> {{-1, 0, 0}, {0, 1, 0}},
AbsoluteOptions[fig]], axesLabels,
Epilog -> Text[Style["Panel A", Bold, Black, 12], ImageScaled[{0.075, 0.975}]]
];
fig = Show[fig, AxesStyle -> Directive[Opacity[0]]];
Row[{fig, axes}]
На этом этапе вы должны увидеть это:
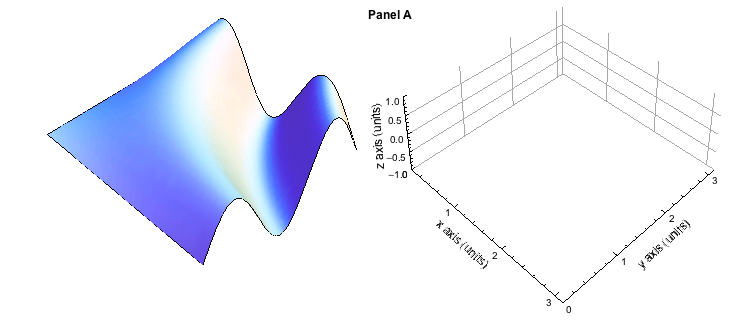
Увеличение заботится о разрешении вашего изображения. Вы должны попробовать разные значения, чтобы увидеть, как это меняет вашу картину.
fig = Magnify[fig, 5];
fig = Rasterize[fig, Background -> None];
Объединить графику
axes = First@ImportString[ExportString[axes, "PDF"], "PDF"];
result = Show[axes, Epilog -> Inset[fig, {0, 0}, {0, 0}, ImageDimensions[axes]]];
Экспортировать их
Export["Result.pdf", result];
Export["Result.eps", result];
Единственное различие, которое я обнаружил между M7 и M8 с помощью приведенного выше кода, заключается в том, что M7 неправильно экспортирует файл eps. Кроме того, теперь все работает нормально.:)
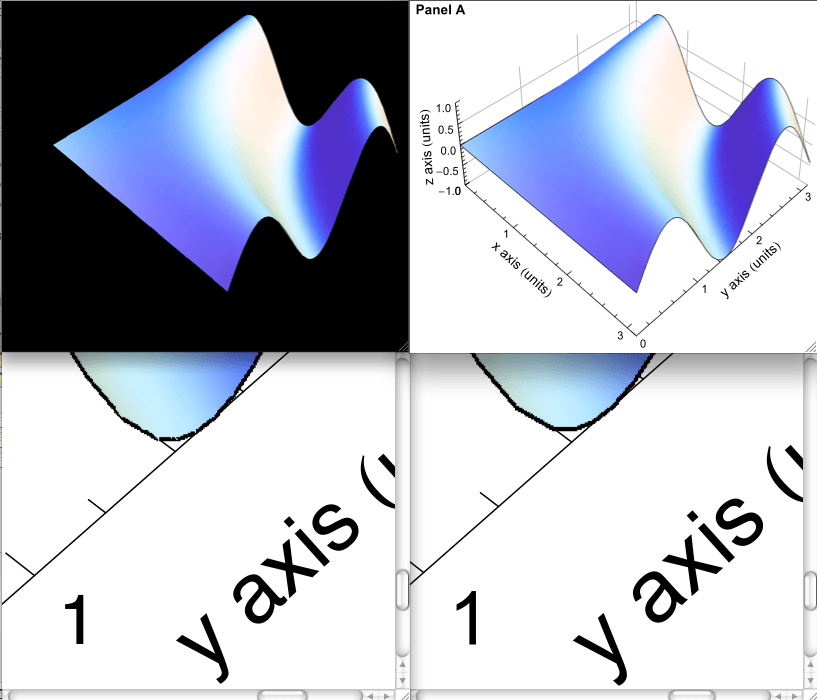
Первый столбец показывает вывод, полученный из M7. Сверху - версия в формате eps с размером файла 614 КБ, снизу - версия в формате PDF с размером файла 455 КБ. Второй столбец показывает вывод, полученный из M8. Сверху - версия eps с размером файла 643 КБ, снизу - версия PDF с размером файла 463 КБ.
Я надеюсь, что вы найдете это полезным. Пожалуйста, проверьте ответ Алексея, чтобы увидеть комментарии в его коде, они помогут вам избежать ловушек с Mathematica.
6 ответов
Полное решение для Mathematica 7.0.1: исправление ошибок
Код с комментариями:
(*controls the resolution of rasterized graphics*)
magnification = 5;
SetOptions[$FrontEnd, PrintingStyleEnvironment -> "Working"]
(*Turn off history for saving memory*)
$HistoryLength = 0;
(*Epilog will give us the bounding box of the graphics*)
g1 = Plot3D[Sin[x y], {x, 0, Pi}, {y, 0, Pi},
AlignmentPoint -> Center, AspectRatio -> 0.925,
Axes -> {True, True, True},
AxesEdge -> {{-1, -1}, {1, -1}, {-1, -1}},
BaseStyle -> {FontFamily -> "Arial", FontSize -> 12},
Boxed -> False, BoxRatios -> {3, 3, 1},
LabelStyle -> Directive[Black], ImagePadding -> All,
ImageSize -> 5*72, PlotRange -> All, PlotRangePadding -> None,
TicksStyle -> Directive[10], ViewPoint -> {2, -2, 2},
ViewVertical -> {0, 0, 1}, AxesStyle -> Directive[Opacity[0]],
FaceGrids -> {{-1, 0, 0}, {0, 1, 0}}, Mesh -> None,
ImagePadding -> 40,
Epilog -> {Red, AbsoluteThickness[1],
Line[{ImageScaled[{0, 0}], ImageScaled[{0, 1}],
ImageScaled[{1, 1}], ImageScaled[{1, 0}],
ImageScaled[{0, 0}]}]}];
(*The options list should NOT contain ImagePadding->Full.Even it is \
before ImagePadding->40 it is not replaced by the latter-another bug!*)
axes = Graphics3D[{Opacity[0],
Point[PlotRange /. AbsoluteOptions[g1] // Transpose]},
AlignmentPoint -> Center, AspectRatio -> 0.925,
Axes -> {True, True, True},
AxesEdge -> {{-1, -1}, {1, -1}, {-1, -1}},
AxesStyle -> Directive[10, Black],
BaseStyle -> {FontFamily -> "Arial", FontSize -> 12},
Boxed -> False, BoxRatios -> {3, 3, 1},
LabelStyle -> Directive[Black], ImageSize -> 5*72,
PlotRange -> All, PlotRangePadding -> None,
TicksStyle -> Directive[10], ViewPoint -> {2, -2, 2},
ViewVertical -> {0, 0, 1}, ImagePadding -> 40,
Epilog -> {Red, AbsoluteThickness[1],
Line[{ImageScaled[{0, 0}], ImageScaled[{0, 1}],
ImageScaled[{1, 1}], ImageScaled[{1, 0}],
ImageScaled[{0, 0}]}]}];
(*fixing bug with ImagePadding loosed when specifyed as option in \
Plot3D*)
g1 = AppendTo[g1, ImagePadding -> 40];
(*Increasing ImageSize without damage.Explicit setting for \
ImagePadding is important (due to a bug in behavior of \
ImagePadding->Full)!*)
g1 = Magnify[g1, magnification];
g2 = Rasterize[g1, Background -> None];
(*Fixing bug with non-working option Background->None when graphics \
is Magnifyed*)
g2 = g2 /. {255, 255, 255, 255} -> {0, 0, 0, 0};
(*Fixing bug with icorrect exporting of Ticks in PDF when Graphics3D \
and 2D Raster are combined*)
axes = First@ImportString[ExportString[axes, "PDF"], "PDF"];
(*Getting explicid ImageSize of graphics imported form PDF*)
imageSize =
Last@Transpose[{First@#, Last@#} & /@
Sort /@ Transpose@
First@Cases[axes,
Style[{Line[x_]}, ___, RGBColor[1.`, 0.`, 0.`, 1.`], ___] :>
x, Infinity]]
(*combining Graphics3D and Graphics*)
result = Show[axes, Epilog -> Inset[g2, {0, 0}, {0, 0}, imageSize]]
Export["C:\\result.pdf", result]
Вот что я вижу в тетради:
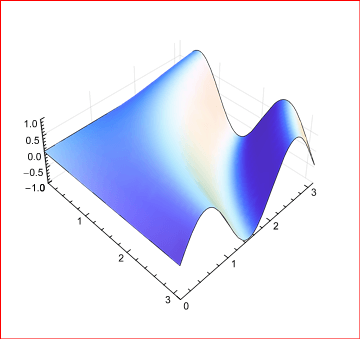
И вот что я получаю в PDF:
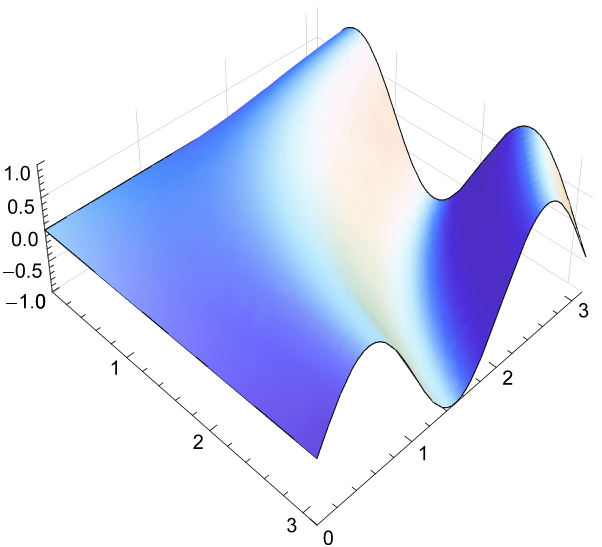
Просто проверяю (Mma8):
SetOptions[$FrontEnd, PrintingStyleEnvironment -> "Working"];
in = 72;
G3D = Graphics3D[AlignmentPoint -> Center, AspectRatio -> 0.925,
Axes -> {True, True, True},
AxesEdge -> {{-1, -1}, {1, -1}, {-1, -1}},
AxesStyle -> Directive[10, Black],
BaseStyle -> {FontFamily -> "Arial", FontSize -> 12},
Boxed -> False, BoxRatios -> {3, 3, 1},
LabelStyle -> Directive[Black], ImagePadding -> All,
ImageSize -> 5 in, PlotRange -> All, PlotRangePadding -> None,
TicksStyle -> Directive[10], ViewPoint -> {2, -2, 2},
ViewVertical -> {0, 0, 1}];
g = Show[Plot3D[Sin[x y], {x, 0, Pi}, {y, 0, Pi}, Mesh -> None,
AxesLabel -> {"x", "y", "z"}], Options[G3D]];
axes = Graphics3D[{}, AbsoluteOptions[g]];
fig = Show[g, AxesStyle -> Directive[Opacity[0]],
FaceGrids -> {{-1, 0, 0}, {0, 1, 0}}];
Export["c:\\Axes.pdf", axes, Background -> None];
Export["c:\\Fig.pdf", Rasterize[fig, ImageResolution -> 300]];
a = Import["c:\\Axes.pdf"];
b = Import["c:\\Fig.pdf"];
Export["c:\\FinalFig.pdf", Show[b, a]]
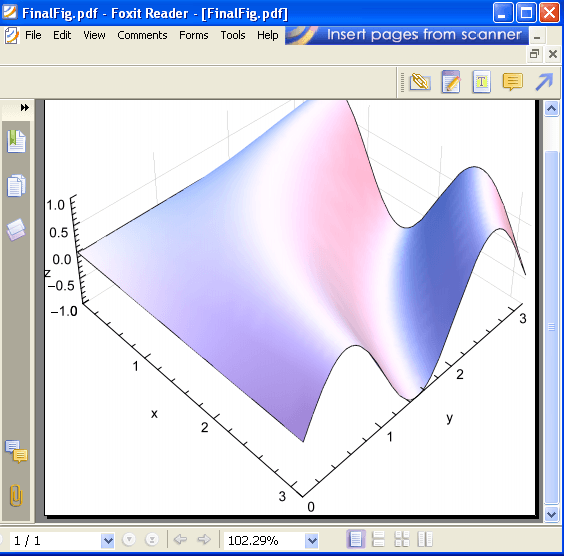
Здесь я представляю другую версию исходного решения, которая использует второй аргумент Raster вместо Inset, Я думаю, что этот путь немного проще.
Вот код из раздела ОБНОВЛЕНИЕ вопроса (немного изменен):
SetOptions[$FrontEnd, PrintingStyleEnvironment -> "Working"];
$HistoryLength = 0;
in = 72;
G3D = Graphics3D[AlignmentPoint -> Center, AspectRatio -> 0.925,
Axes -> {True, True, True},
AxesEdge -> {{-1, -1}, {1, -1}, {-1, -1}},
AxesStyle -> Directive[10, Black],
BaseStyle -> {FontFamily -> "Arial", FontSize -> 12},
Boxed -> False, BoxRatios -> {3, 3, 1},
LabelStyle -> Directive[Black], ImagePadding -> 40,
ImageSize -> 5 in, PlotRange -> All, PlotRangePadding -> 0,
TicksStyle -> Directive[10], ViewPoint -> {2, -2, 2},
ViewVertical -> {0, 0, 1}];
axesLabels =
Graphics3D[{Text[Style["x axis (units)", Black, 12],
Scaled[{.5, -.1, 0}], {0, 0}, {1, -.9}],
Text[Style["y axis (units)", Black, 12],
Scaled[{1.1, .5, 0}], {0, 0}, {1, .9}],
Text[Style["z axis (units)", Black, 12],
Scaled[{0, -.15, .7}], {0, 0}, {-.1, 1.5}]}];
fig = Show[Plot3D[Sin[x y], {x, 0, Pi}, {y, 0, Pi}, Mesh -> None],
ImagePadding -> {{40, 0}, {15, 0}}, Options[G3D]];
axes = Show[
Graphics3D[{}, FaceGrids -> {{-1, 0, 0}, {0, 1, 0}},
AbsoluteOptions[fig]], axesLabels,
Prolog ->
Text[Style["Panel A", Bold, Black, 12],
ImageScaled[{0.075, 0.975}]]];
fig = Show[fig, AxesStyle -> Directive[Opacity[0]]];
fig = Magnify[fig, 5];
fig = Rasterize[fig, Background -> None];
axes2D = First@ImportString[ExportString[axes, "PDF"], "PDF"];
Остальная часть ответа - новое решение.
Сначала мы устанавливаем второй аргумент Raster так что он заполнит полный PlotRange из axes2D, Общий способ сделать это:
fig = fig /.
Raster[data_, rectangle_, opts___] :>
Raster[data, {Scaled[{0, 0}], Scaled[{1, 1}]}, opts];
Другой способ - сделать прямое назначение на соответствующий Part оригинального выражения:
fig[[1, 2]] = {Scaled[{0, 0}], Scaled[{1, 1}]}
Обратите внимание, что этот последний код основан на знании внутренней структуры выражения, сгенерированного Rasterize который потенциально зависит от версии.
Теперь мы объединяем два графических объекта очень простым способом:
result = Show[axes2D, fig]
И экспортируем результат:
Export["C:/Result.pdf", result];
Export["C:/Result.eps", result];
И.eps, и.pdf отлично экспортируются с Mathematica 8.0.4 под Windows XP 32 бит и выглядят идентично файлам, экспортированным с оригинальным кодом:
result = Show[axes2D,
Epilog -> Inset[fig, Center, Center, ImageScaled[{1, 1}]]]
Export["C:/Result.pdf", result];
Export["C:/Result.eps", result];
Обратите внимание, что нам не обязательно конвертировать axes на контуры хотя бы при экспорте в PDF. Код
result = Show[axes,
Epilog -> Inset[fig, Center, Center, ImageScaled[{1, 1}]]]
Export["C:/Result.pdf", result];
и код
fig[[1, 2]] = {ImageScaled[{0, 0}], ImageScaled[{1, 1}]};
result = Show[axes, Epilog -> First@fig]
Export["C:/Result.pdf", result];
создавать PDF-файлы, похожие на обе предыдущие версии.
В Mathematica 8 эта проблема может быть решена еще проще с использованием новых Overlay функция.
Вот код из раздела ОБНОВЛЕНИЕ вопроса:
SetOptions[$FrontEnd, PrintingStyleEnvironment -> "Working"];
$HistoryLength = 0;
in = 72;
G3D = Graphics3D[AlignmentPoint -> Center, AspectRatio -> 0.925,
Axes -> {True, True, True},
AxesEdge -> {{-1, -1}, {1, -1}, {-1, -1}},
AxesStyle -> Directive[10, Black],
BaseStyle -> {FontFamily -> "Arial", FontSize -> 12},
Boxed -> False, BoxRatios -> {3, 3, 1},
LabelStyle -> Directive[Black], ImagePadding -> 40,
ImageSize -> 5 in, PlotRange -> All, PlotRangePadding -> 0,
TicksStyle -> Directive[10], ViewPoint -> {2, -2, 2},
ViewVertical -> {0, 0, 1}];
axesLabels =
Graphics3D[{Text[Style["x axis (units)", Black, 12],
Scaled[{.5, -.1, 0}], {0, 0}, {1, -.9}],
Text[Style["y axis (units)", Black, 12],
Scaled[{1.1, .5, 0}], {0, 0}, {1, .9}],
Text[Style["z axis (units)", Black, 12],
Scaled[{0, -.15, .7}], {0, 0}, {-.1, 1.5}]}];
fig = Show[Plot3D[Sin[x y], {x, 0, Pi}, {y, 0, Pi}, Mesh -> None],
ImagePadding -> {{40, 0}, {15, 0}}, Options[G3D]];
axes = Show[
Graphics3D[{}, FaceGrids -> {{-1, 0, 0}, {0, 1, 0}},
AbsoluteOptions[fig]], axesLabels,
Epilog ->
Text[Style["Panel A", Bold, Black, 12],
ImageScaled[{0.075, 0.975}]]];
fig = Show[fig, AxesStyle -> Directive[Opacity[0]]];
И вот решение:
gr = Overlay[{axes,
Rasterize[fig, Background -> None, ImageResolution -> 300]}]
Export["Result.pdf", gr]
В этом случае нам не нужно конвертировать шрифты в контуры.
ОБНОВИТЬ
Как указал в комментариях к этому ответу jmlopez, опция Background -> None не работает должным образом под Mac OS X в Mathematica 8.0.1. Один из обходных путей - заменить белые непрозрачные точки прозрачными:
gr = Overlay[{axes,
Rasterize[fig, Background -> None,
ImageResolution -> 300] /. {255, 255, 255, 255} -> {0, 0, 0, 0}}]
Export["Result.pdf", gr]
Это выглядит как много шума из ничего. Насколько я понимаю, проблема, которую вы хотите решить, заключается в следующем:
- Вы хотите экспортировать в векторный формат, чтобы при печати использовалось оптимальное разрешение для шрифтов, линий и графики.
- В вашей программе редактирования вы не хотите, чтобы вас беспокоила медлительность рендеринга сложной векторной графики
Этим требованиям можно удовлетворить, экспортировав в формате.eps и используя встроенное растровое изображение для предварительного просмотра.
Export["file.eps","PreviewFormat"->"TIFF"]
Это будет работать во многих приложениях. К сожалению, eps-фильтр MS Word сильно изменился за последние четыре версии или около того, и хотя однажды он работал для меня в одной из старых функций, он больше не работает в W2010. Я слышал слухи, что это может работать в Mac-версии, но я не могу проверить прямо сейчас.
Mathematica 9.0.1.0 / 64-bit Linux: В общем, очень сложно разместить векторизованные оси в правильном положении. В большинстве приложений достаточно просто растеризовать все с высоким разрешением:
fig = Plot3D[Sin[x y], {x, 0, 3}, {y, 0, 3}, Mesh -> None];
Export["export.eps", fig, "AllowRasterization" -> True,
ImageResolution -> 600];
Код экспортирует графику в EPS-файл, используя высококачественную растеризацию как 3D-контента, так и оси. Наконец, вы можете преобразовать EPS-файл в PDF, используя, например, команду Linux epspdf:
epspdf export.eps
Это, вероятно, достаточно для большинства пользователей и экономит много времени. Однако, если вы действительно хотите экспортировать текст в виде векторной графики, вы можете попробовать следующую функцию:
ExportAsSemiRaster[filename_, dpi_, fig_, plotrange_,
plotrangepadding_] := (
range =
Show[fig, PlotRange -> plotrange,
PlotRangePadding -> plotrangepadding];
axes = Show[Graphics3D[{}, AbsoluteOptions[range]]];
noaxes = Show[range, AxesStyle -> Transparent];
raster =
Rasterize[noaxes, Background -> None, ImageResolution -> dpi];
result =
Show[raster,
Epilog -> Inset[axes, Center, Center, ImageDimensions[raster]]];
Export[filename, result];
);
Вам необходимо явно указать PlotRange и PlotRangePadding. Пример:
fig = Graphics3D[{Opacity[0.9], Orange,
Polygon[{{0, 0, 0}, {4, 0, 4}, {4, 5, 7}, {0, 5, 5}}],
Opacity[0.05], Gray, CuboidBox[{0, 0, 0}, {4, 5, 7}]},
Axes -> True, AxesStyle -> Darker[Orange],
AxesLabel -> {"x1", "x2", "x3"}, Boxed -> False,
ViewPoint -> {-8.5, -8, 6}];
ExportAsSemiRaster["export.pdf", 600,
fig, {{0, 4}, {0, 5}, {0, 7}}, {.0, .0, .0}];
Print[Import["export.pdf"]];