mgcv: как сделать ступенчатую регрессию с моделью ответа Твиди?
У кого-нибудь есть идеи, как сделать ступенчатую регрессию с помощью Tweedie в R?
Я нашел mgcv пакет, который, очевидно, рассматривает параметр мощности Твиди как еще один параметр, который будет оценен. Это, кажется, улучшает необходимость использования tweedie.profile оценить силу за пределами glmТаким образом, кажется целесообразным использовать автоматическую пошаговую функцию для регрессии. Но я не смог выяснить, если пакет также предлагает пошаговую функцию. В руководстве по упаковке есть, что сказать.
Я заблудился в разговоре о сглаживаниях:
В пакете mgcv нет step.gam.
Чтобы упростить полностью автоматический выбор модели, в пакете реализованы два метода плавного изменения, которые можно использовать, чтобы сгладить сглаживание до нуля как часть выбора сглаживания.
Буду признателен за вашу помощь. Благодарю.
1 ответ
Ваш вопрос не относится к "семье Твиди"; это общее mgcv особенность в выборе модели.
mgcv не использует step.gam для выбора модели. Я думаю, что ваша путаница исходит от другого пакета gam, который бы использовал step.gam последовательно добавить / удалить термин и отчеты AIC. Когда ты пойдешь ?step.gam в mgcv, это относится к вам ?gam.selection, ?step.gam намеренно оставлен там, в случае, если люди ищут это. Но все детали приведены в ?gam.selection,
Там нет необходимости делать step.gam в mgcv , Оценка модели и выбор модели интегрированы в mgcv , Для штрафного сплайна регрессии / сглаживания, когда параметр сглаживания стремится к бесконечности (очень большой), его вторая производная штрафуется до нуля, оставляя простой линейный член. Например, если мы укажем такую модель:
y ~ s(x1, bs = 'cr') + s(x2, bs = 'cr')
в то время как s(x2) является ложным модельным термином и не должен быть включен в модель, тогда mgcv:::gam/bam будет сокращаться s(x2) в x2 после оценки получается модель типа:
y ~ s(x1) + x2
Это значит, когда вы используете plot.gam() проверить предполагаемую гладкую функцию для каждого модельного члена, s(x1) кривая, но s(x2) это прямая линия
Теперь это не совсем удовлетворительно. Для полного, успешного выбора модели, мы хотим отказаться x2 а также, т.е. s(x2) до 0, чтобы получить обозначение модели:
y ~ s(x1)
Но этого нетрудно достичь. Мы можем использовать усадку гладкого класса bs = 'ts' (усадка тонкой пластины регрессии сплайна, в отличие от обычного tp) или же bs = cs' (усадочный кубический регрессионный сплайн, в отличие от обычного 'cr'), и mgcv:::gam/bam должен быть в состоянии сжаться s(x2) до 0. Математика за этим, что mgcv изменит собственные значения линейного члена (то есть, нулевое пространство) от 0 до 0,1, маленькое, но положительное число, так, чтобы наказание вступило в силу для линейного члена. В результате, когда вы делаете plot.gam(), ты увидишь s(x2) горизонтальная линия на 0.
bs = 'cs' или же bs = 'ts' должны быть введены в действие s(); еще mgcv также позволяет вам покинуть bs = 'cr' или же bs = 'tp' нетронутым в s(), но поставить select = TRUE в gam() или же bam(), select = TRUE это более общий подход, так как усадка сглаживает только класс cs а также ts, в то время как select = TRUE работать для всех видов гладкой спецификации. По сути, они делают то же самое, увеличивая 0 собственных значений до 0,1.
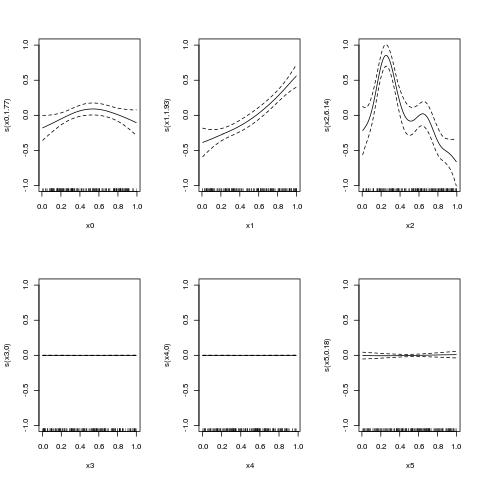
Следующий пример взят из примера под ?gam.selection, Обратите внимание, как select = TRUE сжимает несколько терминов до 0, давая информативный выбор модели.
library(mgcv)
set.seed(3);n<-200
dat <- gamSim(1,n=n,scale=.15,dist="poisson") ## simulate data
dat$x4 <- runif(n, 0, 1);dat$x5 <- runif(n, 0, 1) ## spurious
b <- gam(y~s(x0)+s(x1)+s(x2)+s(x3)+s(x4)+s(x5),data=dat,
family=poisson,select=TRUE,method="REML")
summary(b)
plot.gam(b,pages=1)
Обратите внимание, что p-values в summary.gam() Также приводятся доказательства такого выбора:
Approximate significance of smooth terms:
edf Ref.df Chi.sq p-value
s(x0) 1.7655119 9 5.264 0.0397 *
s(x1) 1.9271039 9 65.356 <2e-16 ***
s(x2) 6.1351372 9 156.204 <2e-16 ***
s(x3) 0.0002618 9 0.000 0.4088
s(x4) 0.0002766 9 0.000 1.0000
s(x5) 0.1757146 9 0.195 0.2963
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
R-sq.(adj) = 0.545 Deviance explained = 51.6%
-REML = 430.78 Scale est. = 1 n = 200