Почему foreach %dopar% замедляется с каждым дополнительным узлом?
Я написал простое умножение матриц, чтобы проверить возможности многопоточности / распараллеливания моей сети, и заметил, что вычисления выполняются намного медленнее, чем ожидалось.
Тест прост: умножьте 2 матрицы (4096x4096) и верните время вычисления. Ни матрицы, ни результаты не сохраняются. Время вычислений не является тривиальным (50-90 сек в зависимости от вашего процессора).
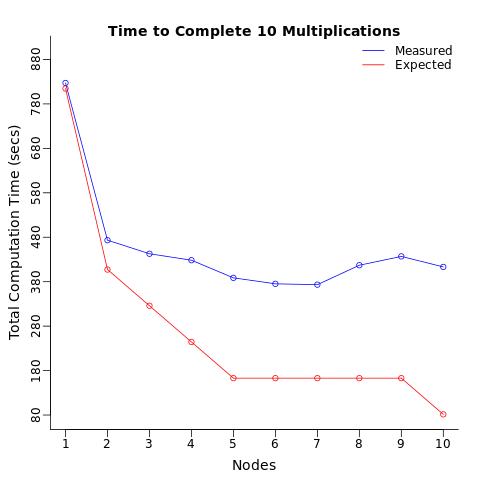
Условия: Я повторил это вычисление 10 раз, используя 1 процессор, разделив эти 10 вычислений на 2 процессора (по 5 в каждом), затем 3 процессора, ... до 10 процессоров (1 вычисление для каждого процессора). Я ожидал, что общее время вычислений будет постепенно сокращаться, и я ожидал, что 10 процессоров выполнят вычисления в 10 раз быстрее, чем один процессор, чтобы сделать то же самое.
Результаты: Вместо этого я получил только 2-кратное сокращение времени вычислений, что в 5 раз МЕДЛЕННО, чем ожидалось.
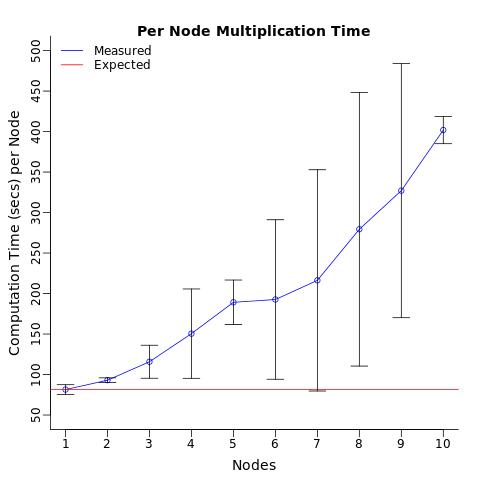
Когда я вычислял среднее время вычислений на узел, я ожидал, что каждый процессор будет вычислять тест в одно и то же время (в среднем) независимо от количества назначенных процессоров. Я был удивлен, увидев, что простая отправка одной и той же операции нескольким процессорам замедляет среднее время вычислений каждого процессора.
Кто-нибудь может объяснить, почему это происходит?
Обратите внимание, что это вопрос не является дубликатом этих вопросов:
foreach% dopar% медленнее, чем для цикла
или же
Почему параллельный пакет медленнее, чем просто применение apply?
Потому что тестовое вычисление не является тривиальным (то есть 50-90 сек, а не 1-2 сек), и потому что нет никакой связи между процессорами, которые я могу видеть (то есть никакие результаты не возвращаются или сохраняются, кроме времени вычисления).
Я приложил сценарии и функции ниже для репликации.
library(foreach); library(doParallel);library(data.table)
# functions adapted from
# http://www.bios.unc.edu/research/genomic_software/Matrix_eQTL/BLAS_Testing.html
Matrix.Multiplier <- function(Dimensions=2^12){
# Creates a matrix of dim=Dimensions and runs multiplication
#Dimensions=2^12
m1 <- Dimensions; m2 <- Dimensions; n <- Dimensions;
z1 <- runif(m1*n); dim(z1) = c(m1,n)
z2 <- runif(m2*n); dim(z2) = c(m2,n)
a <- proc.time()[3]
z3 <- z1 %*% t(z2)
b <- proc.time()[3]
c <- b-a
names(c) <- NULL
rm(z1,z2,z3,m1,m2,n,a,b);gc()
return(c)
}
Nodes <- 10
Results <- NULL
for(i in 1:Nodes){
cl <- makeCluster(i)
registerDoParallel(cl)
ptm <- proc.time()[3]
i.Node.times <- foreach(z=1:Nodes,.combine="c",.multicombine=TRUE,
.inorder=FALSE) %dopar% {
t <- Matrix.Multiplier(Dimensions=2^12)
}
etm <- proc.time()[3]
i.TotalTime <- etm-ptm
i.Times <- cbind(Operations=Nodes,Node.No=i,Avr.Node.Time=mean(i.Node.times),
sd.Node.Time=sd(i.Node.times),
Total.Time=i.TotalTime)
Results <- rbind(Results,i.Times)
rm(ptm,etm,i.Node.times,i.TotalTime,i.Times)
stopCluster(cl)
}
library(data.table)
Results <- data.table(Results)
Results[,lower:=Avr.Node.Time-1.96*sd.Node.Time]
Results[,upper:=Avr.Node.Time+1.96*sd.Node.Time]
Exp.Total <- c(Results[Node.No==1][,Avr.Node.Time]*10,
Results[Node.No==1][,Avr.Node.Time]*5,
Results[Node.No==1][,Avr.Node.Time]*4,
Results[Node.No==1][,Avr.Node.Time]*3,
Results[Node.No==1][,Avr.Node.Time]*2,
Results[Node.No==1][,Avr.Node.Time]*2,
Results[Node.No==1][,Avr.Node.Time]*2,
Results[Node.No==1][,Avr.Node.Time]*2,
Results[Node.No==1][,Avr.Node.Time]*2,
Results[Node.No==1][,Avr.Node.Time]*1)
Results[,Exp.Total.Time:=Exp.Total]
jpeg("Multithread_Test_TotalTime_Results.jpeg")
par(oma=c(0,0,0,0)) # set outer margin to zero
par(mar=c(3.5,3.5,2.5,1.5)) # number of lines per margin (bottom,left,top,right)
plot(x=Results[,Node.No],y=Results[,Total.Time], type="o", xlab="", ylab="",ylim=c(80,900),
col="blue",xaxt="n", yaxt="n", bty="l")
title(main="Time to Complete 10 Multiplications", line=0,cex.lab=3)
title(xlab="Nodes",line=2,cex.lab=1.2,
ylab="Total Computation Time (secs)")
axis(2, at=seq(80, 900, by=100), tick=TRUE, labels=FALSE)
axis(2, at=seq(80, 900, by=100), tick=FALSE, labels=TRUE, line=-0.5)
axis(1, at=Results[,Node.No], tick=TRUE, labels=FALSE)
axis(1, at=Results[,Node.No], tick=FALSE, labels=TRUE, line=-0.5)
lines(x=Results[,Node.No],y=Results[,Exp.Total.Time], type="o",col="red")
legend('topright','groups',
legend=c("Measured", "Expected"), bty="n",lty=c(1,1),
col=c("blue","red"))
dev.off()
jpeg("Multithread_Test_PerNode_Results.jpeg")
par(oma=c(0,0,0,0)) # set outer margin to zero
par(mar=c(3.5,3.5,2.5,1.5)) # number of lines per margin (bottom,left,top,right)
plot(x=Results[,Node.No],y=Results[,Avr.Node.Time], type="o", xlab="", ylab="",
ylim=c(50,500),col="blue",xaxt="n", yaxt="n", bty="l")
title(main="Per Node Multiplication Time", line=0,cex.lab=3)
title(xlab="Nodes",line=2,cex.lab=1.2,
ylab="Computation Time (secs) per Node")
axis(2, at=seq(50,500, by=50), tick=TRUE, labels=FALSE)
axis(2, at=seq(50,500, by=50), tick=FALSE, labels=TRUE, line=-0.5)
axis(1, at=Results[,Node.No], tick=TRUE, labels=FALSE)
axis(1, at=Results[,Node.No], tick=FALSE, labels=TRUE, line=-0.5)
abline(h=Results[Node.No==1][,Avr.Node.Time], col="red")
epsilon = 0.2
segments(Results[,Node.No],Results[,lower],Results[,Node.No],Results[,upper])
segments(Results[,Node.No]-epsilon,Results[,upper],
Results[,Node.No]+epsilon,Results[,upper])
segments(Results[,Node.No]-epsilon, Results[,lower],
Results[,Node.No]+epsilon,Results[,lower])
legend('topleft','groups',
legend=c("Measured", "Expected"), bty="n",lty=c(1,1),
col=c("blue","red"))
dev.off()
РЕДАКТИРОВАТЬ: Ответ @Hong Ooi комментарий
я использовал lscpu в UNIX получить;
Architecture: x86_64
CPU op-mode(s): 32-bit, 64-bit
Byte Order: Little Endian
CPU(s): 30
On-line CPU(s) list: 0-29
Thread(s) per core: 1
Core(s) per socket: 1
Socket(s): 30
NUMA node(s): 4
Vendor ID: GenuineIntel
CPU family: 6
Model: 63
Model name: Intel(R) Xeon(R) CPU E5-2630 v3 @ 2.40GHz
Stepping: 2
CPU MHz: 2394.455
BogoMIPS: 4788.91
Hypervisor vendor: VMware
Virtualization type: full
L1d cache: 32K
L1i cache: 32K
L2 cache: 256K
L3 cache: 20480K
NUMA node0 CPU(s): 0-7
NUMA node1 CPU(s): 8-15
NUMA node2 CPU(s): 16-23
NUMA node3 CPU(s): 24-29
РЕДАКТИРОВАТЬ: Ответ на комментарий @Steve Weston.
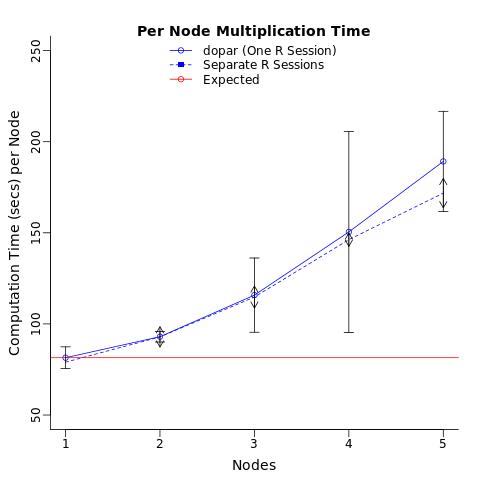
Я использую сеть виртуальной машины (но я не администратор) с доступом до 30 кластеров. Я провел тест, который вы предложили. Открыл 5 R сессий и запустил умножение матриц на 1,2...5 одновременно (или так быстро, как я мог перебирать и выполнять). Получили результаты, очень похожие на предыдущие (повторение: каждый дополнительный процесс замедляет все отдельные сеансы). Обратите внимание, я проверил использование памяти с помощью top а также htop и использование никогда не превышало 5% емкости сети (~2,5/64 ГБ).
ВЫВОДЫ:
Проблема, кажется, специфична для R. Когда я запускаю другие многопоточные команды с другим программным обеспечением (например, PLINK), я не сталкиваюсь с этой проблемой, и параллельный процесс запускается, как ожидалось. Я также попытался запустить выше с Rmpi а также doMPI с такими же (более медленными) результатами. Проблема, кажется, связана R сеансы / распараллеленные команды в сети виртуальных машин. Что мне действительно нужно помочь, так это как определить проблему. Подобная проблема, кажется, здесь указана
3 ответа
Я нахожу время умножения на узел очень интересным, потому что время не включает в себя какие-либо издержки, связанные с параллельным циклом, а только время для выполнения умножения матриц, и они показывают, что время увеличивается с числом умножений матриц выполняется параллельно на той же машине.
Я могу думать о двух причинах, почему это могло произойти:
- Пропускная способность памяти машины насыщается умножением матриц до того, как вы исчерпаете ядра;
- Матрица умножения многопоточная.
Вы можете проверить первую ситуацию, запустив несколько сеансов R (я делал это в нескольких терминалах), создав две матрицы в каждом сеансе:
> x <- matrix(rnorm(4096*4096), 4096)
> y <- matrix(rnorm(4096*4096), 4096)
и затем выполнение умножения матриц в каждом из этих сеансов примерно в одно и то же время:
> system.time(z <- x %*% t(y))
В идеале, это время должно быть одинаковым независимо от количества R-сессий, которые вы используете (вплоть до количества ядер), но, поскольку умножение матриц является довольно трудоемкой операцией, многие машины исчерпают пропускную способность памяти, прежде чем они исчерпают ядра, в результате чего время увеличивается.
Если ваша установка R была построена с использованием многопоточной математической библиотеки, такой как MKL или ATLAS, то вы могли бы использовать все свои ядра с умножением в одну матрицу, поэтому вы не можете ожидать повышения производительности, используя несколько процессов, если вы не используете несколько компьютеров.
Вы можете использовать инструмент, такой как "top", чтобы увидеть, используете ли вы многопоточную математическую библиотеку.
Наконец, выход из lscpu предполагает, что вы используете виртуальную машину. Я никогда не проводил тестирование производительности на многоядерных виртуальных машинах, но это также может быть источником проблем.
Обновить
Я полагаю, что причина, по которой ваши параллельные умножения матриц выполняются медленнее, чем умножение одиночных матриц, заключается в том, что ваш ЦП не способен читать память достаточно быстро, чтобы загружать более двух ядер на полной скорости, что я назвал насыщением пропускной способности вашей памяти., Если у вашего процессора достаточно большой кэш, вы можете избежать этой проблемы, но на самом деле он не имеет никакого отношения к объему памяти на материнской плате.
Я думаю, что это всего лишь ограничение использования одного компьютера для параллельных вычислений. Одним из преимуществ использования кластера является то, что увеличивается пропускная способность вашей памяти, а также общая совокупная память. Таким образом, если вы запустили одно или два умножения матриц на каждом узле многоузловой параллельной программы, вы не столкнулись бы с этой конкретной проблемой.
Предполагая, что у вас нет доступа к кластеру, вы можете попробовать на компьютере тестирование многопоточной математической библиотеки, такой как MKL или ATLAS. Вполне возможно, что вы могли бы добиться более высокой производительности, запустив одну многопоточную матрицу, чем параллельно запустив их в нескольких процессах. Но будьте осторожны при использовании как многопоточной математической библиотеки, так и пакета параллельного программирования.
Вы также можете попробовать использовать графический процессор. Они явно хороши в умножении матриц.
Обновление 2
Чтобы увидеть, если проблема связана с R, я предлагаю вам сравнить dgemm функция, которая является функцией BLAS, используемой R для реализации умножения матриц.
Вот простая программа Fortran для сравнения dgemm, Я предлагаю выполнить его с нескольких терминалов так же, как я описал для бенчмаркинга %*% в R:
program main
implicit none
integer n, i, j
integer*8 stime, etime
parameter (n=4096)
double precision a(n,n), b(n,n), c(n,n)
do i = 1, n
do j = 1, n
a(i,j) = (i-1) * n + j
b(i,j) = -((i-1) * n + j)
c(i,j) = 0.0d0
end do
end do
stime = time8()
call dgemm('N','N',n,n,n,1.0d0,a,n,b,n,0.0d0,c,n)
etime = time8()
print *, etime - stime
end
На моей машине с Linux один экземпляр запускается за 82 секунды, а четыре экземпляра - за 116 секунд. Это согласуется с результатами, которые я вижу в R, и с моим предположением, что это проблема пропускной способности памяти.
Вы также можете связать это с различными библиотеками BLAS, чтобы увидеть, какая реализация лучше работает на вашем компьютере.
Вы также можете получить некоторую полезную информацию о пропускной способности памяти вашей сети виртуальных машин, используя pmbw - Parallel Memory Bandwidth Benchmark, хотя я никогда не использовал ее.
Я думаю, что очевидный ответ здесь правильный. Умножение матриц не стыдно параллельно. И вы, похоже, не модифицировали код последовательного умножения для его распараллеливания.
Вместо этого вы умножаете две матрицы. Поскольку умножение каждой матрицы, вероятно, обрабатывается только одним ядром, каждое ядро, превышающее два, просто не используется. В результате вы видите улучшение скорости только в 2 раза.
Вы можете проверить это, запустив более 2 умножений матриц. Но я не знаком с foreach, doParallel рамки (я использую parallel Framework), и я не вижу, где в вашем коде изменить это, чтобы проверить его.
Альтернативным тестом является создание параллельной версии умножения матриц, которую я позаимствовал непосредственно из " Параллельных вычислений Matloff для Data Science". Черновик доступен здесь, см. Стр. 27
mmulthread <- function(u, v, w) {
require(parallel)
# determine which rows for this thread
myidxs <- splitIndices(nrow(u), myinfo$nwrkrs ) [[ myinfo$id ]]
# compute this thread's portion of the result
w[myidxs, ] <- u [myidxs, ] %*% v [ , ]
0 # dont return result -- expensive
}
# t e s t on snow c l u s t e r c l s
test <- function (cls, n = 2^5) {
# i n i t Rdsm
mgrinit(cls)
# shared variables
mgrmakevar(cls, "a", n, n)
mgrmakevar(cls, "b", n, n)
mgrmakevar(cls, "c", n, n)
# f i l l i n some t e s t data
a [ , ] <- 1:n
b [ , ] <- rep (1 ,n)
# export function
clusterExport(cls , "mmulthread" )
# run function
clusterEvalQ(cls , mmulthread (a ,b ,c ))
#print ( c[ , ] ) # not p ri n t ( c ) !
}
library(parallel)
library(Rdsm)
c1 <- makeCluster(1)
c2 <- makeCluster (2)
c4 <- makeCluster(4)
c8 <- makeCluster(8)
library(microbenchmark)
microbenchmark(node1= test(c1, n= 2^10),
node2= test(c2, n= 2^10),
node4= test(c4, n= 2^10),
node8= test(c8, n= 2^10))
Unit: milliseconds
expr min lq mean median uq max neval cld
node1 715.8722 780.9861 818.0487 817.6826 847.5353 922.9746 100 d
node2 404.9928 422.9330 450.9016 437.5942 458.9213 589.1708 100 c
node4 255.3105 285.8409 309.5924 303.6403 320.8424 481.6833 100 a
node8 304.6386 328.6318 365.5114 343.0939 373.8573 836.2771 100 b
Как и ожидалось, распараллеливая умножение матриц, мы видим желаемое улучшение затрат, хотя параллельные издержки явно велики.
Я думаю, что здесь уже был дан ответ? foreach% dopar% медленнее, чем для цикла
Я имею в виду немного экстраполяции того же ответа. Так что в основном концепция остается неизменной.
Вот еще один пример, где процесс происходит параллельно (последовательно или вне последовательности). Ответ не ожидает объединения. Его просто повторно использовать тот же результат, отбрасывая одну и ту же переменную. (Точно так же, как простой цикл). Но все равно цикл замедляется в doParallel. Почему foreach() %do% иногда медленнее, чем for?