Математически вычислить простой графический конвейер

Question

Я пытаюсь сделать / понять все основные математические вычисления, необходимые в графическом конвейере для рендеринга простого 2D-изображения из описания 3D-сцены, такой как VRML. Есть ли хороший пример необходимых шагов, таких как преобразование модели (координаты объекта в мировые координаты), преобразование вида (из мировой координаты в координату вида), вычисление нормалей вершин для освещения, отсечение, вычисление экранных координат объектов внутри вида frustum и создание 2D-проекции для расчета отдельных пикселей с цветами.

Answer 1

Я привык к математике рендеринга в стиле OpenGL, поэтому придерживаюсь его (все рендеры используют почти одинаковую математику)

Сначала некоторые термины, чтобы объяснить:

1. Матрица преобразования

   Представляет систему координат в трехмерном пространстве

   double m[16]; // it is 4x4 matrix stored as 1 dimensional array for speed
   m[0]=xx; m[4]=yx; m[ 8]=zx; m[12]=x0;
   m[1]=xy; m[5]=yy; m[ 9]=zy; m[13]=y0;
   m[2]=xz; m[6]=yz; m[10]=zz; m[14]=z0;
   m[3]= 0; m[7]= 0; m[11]= 0; m[15]= 1;
   

   где:

   • X(xx,xy,xz) является единичным вектором X ось в GCS (глобальная система координат)
   • Y(yx,yy,yz) является единичным вектором Y ось в ГКС
   • Z(zx,zy,zz) является единичным вектором Z ось в ГКС
   • P(x0,y0,z0) является источником представленной системы координат в GCS

   Матрица преобразования используется для преобразования координат между GCS и LCS (локальной системой координат)

   • GCS -> LCS: Al = Ag * m;
   • GCS <- LCS: Ag = Al * (m^-1);
   • Al (x,y,z,w=1) 3D- точка в LCS... в однородных координатах
   • Ag (x,y,z,w=1) 3D- точка в GCS... в однородных координатах

   однородная координата w=1 добавлено, чтобы мы могли умножить 3D вектор на матрицу 4х4

   • m матрица преобразования
   • m^-1 матрица обратного преобразования

   В большинстве случаев это m ортонормированный, что означает X,Y,Z векторы перпендикулярны друг другу, и с размером блока это можно использовать для восстановления точности матрицы после поворотов, перемещений и т. д.

   Для получения дополнительной информации см. Понимание матриц однородного преобразования 4x4

2. Визуализировать матрицы

   Обычно используются такие матрицы:

   • model - представляет действительную систему координат визуализированного объекта
   • view - представляет систему координат камеры (Z ось это направление обзора)
   • modelview - модель и вид умножаются вместе
   • normal - такой же как modelview но x0,y0,z0 = 0 для нормальных векторных вычислений
   • texture - манипулировать текстурными координатами для легкой текстурной анимации и воздействовать обычно на единичную матрицу
   • projection - представлять проекции вида камеры ( перспектива, орто,...), он не должен включать в себя никаких поворотов или перемещений, он больше похож на калибровку датчика камеры (в противном случае туман и другие эффекты потерпят неудачу...)

3. Математика рендеринга

   Для рендеринга 3D сцены вам нужны процедуры 2D рендеринга, такие как рисование 2D текстурированного треугольника... Рендеринг преобразует данные 3D сцены в 2D и рендерит их. Существует больше методов, но наиболее распространенным является использование представления граничной модели + рендеринг границы (только поверхность). 3D -> 2D преобразование выполняется проекцией (ортогональной или перспективной) и Z-буфером или Z-сортировкой.

   • Z-буфер прост и естественен для современных gfx HW
   • Z-сортировка выполняется процессором, поэтому она медленнее и требует дополнительной памяти, но это необходимо для правильного рендеринга прозрачных поверхностей.

Таким образом, конвейер выглядит так:

1. получить фактические данные от модели

   • темя v
   • Нормальный n
   • Координата текстуры t
   • Цвет, Туман, координаты и т.д...

2. преобразовать его в соответствующее пространство

   • v=projection*view*model*v... пространство камеры + проекция
   • n=normal*n... глобальное пространство
   • t=texture*t... текстурное пространство

3. клип данные на экран

   Этот шаг не является необходимым, но мешает визуализировать экранные данные для скорости, а также здесь обычно делается выборка лица. Если нормальный вектор визуализированного "треугольника" противоположен, тогда устанавливается правило намотки полигона, тогда игнорировать "треугольник"

4. визуализировать 3D/2D данные

   использовать только v.x,v.y координаты для рендеринга экрана и vz для теста / значения z-буфера также здесь идет разделение перспективы для перспективных проекций

   • v.x/=v.z,vy/=v.z

   Z-буфер работает так: Z-buffer (zed) - это двумерный массив с тем же размером (разрешением), что и экран (scr). Любой пиксель scr[y][x] отображается только if (zed[y][x]>=z) в таком случае scr[y][x]=color; zed[y][x]=z; Условие if может быть другим (оно может изменяться)

   В случае использования треугольников или более высоких примитивов для рендеринга результирующие 2D- примитивы преобразуются в пиксели в процессе, называемом растеризацией, например, так:

   • Алгоритм заполнения треугольника

Для большей ясности вот как это выглядит:

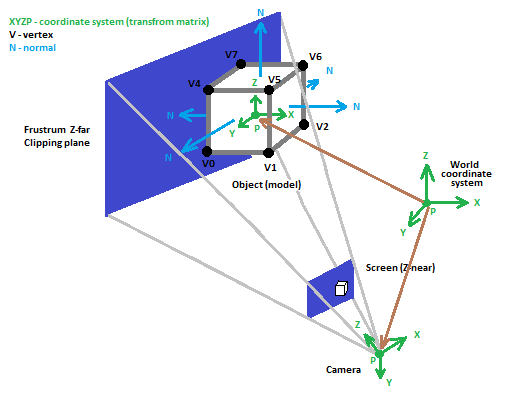
[Заметки]

Матрицы преобразования мультипликативны, так что если вам нужно преобразование N указывает на M матрицы вы можете создать один matrix = m1*m2*...mM и конвертировать N указывает на это в результате matrix только (для скорости). Иногда используются 3x3 матрица преобразования + shift vector вместо 4x4 матрица. в некоторых случаях это быстрее, но вы не можете так просто умножить большее количество преобразований. Для манипулирования матрицами преобразования ищите базовые операции, такие как Rotate или Translate, также есть матрицы для вращений внутри LCS, которые больше подходят для ввода человеком, но они не являются родными для рендеров, таких как OpenGL или DirectX. (потому что они используют обратную матрицу)

Теперь все вышеперечисленное было сделано для стандартного полигонального рендеринга (поверхностное представление объектов на границе). Существуют также другие средства визуализации, такие как объемный рендеринг или (обратная) трассировка лучей и гибридные методы. Также сцена может иметь любую размерность, а не только 3D. Вот некоторые связанные QA, охватывающие эти темы:

• GLSL 3D Объемный задний лучевой трассер
• GLSL 3D Mesh назад raytracer
• 2D Doom / Wolfenstein методы
• Техника рендеринга 4D

Answer 2

Вы можете посмотреть главу 15 из книги " Компьютерная графика: принципы и практика - третье издание " Хьюза и соавторов. Эта глава

Извлекает алгоритмы приведения и растеризации лучей, а затем создает полный исходный код для программного средства трассировки лучей, программного растеризатора и средства визуализации растеризации с аппаратным ускорением.