Как создать круг с кривыми Безье?
У нас есть начальная точка (x, y) и радиус окружности. Также существует механизм, который может создать путь из точек кривой Безье.
Как я могу создать круг, используя кривые Безье?
11 ответов
Как уже говорилось: нет точного представления окружности с использованием кривых Безье.
Чтобы завершить другие ответы: для кривой Безье с n отрезает оптимальное расстояние до контрольных точек в том смысле, что середина кривой лежит на самой окружности, (4/3)*tan(pi/(2n)),
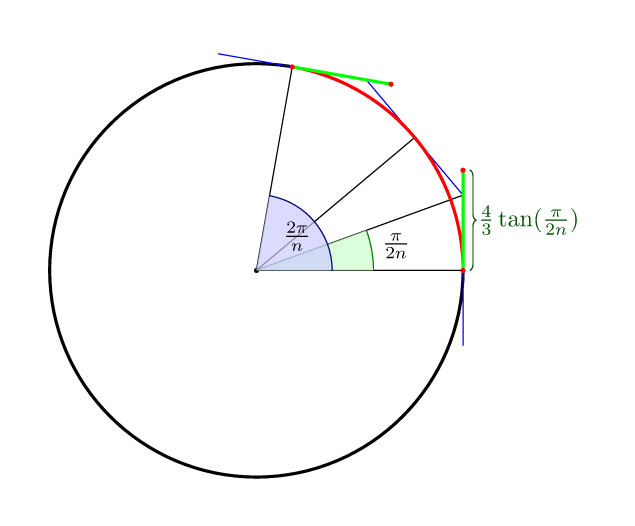
Так что за 4 балла это (4/3)*tan(pi/8) = 4*(sqrt(2)-1)/3 = 0.552284749831,
Охвачено в comp.graphics.faq
Выдержка:
Тема 4.04: Как мне подогнать кривую Безье к кругу?
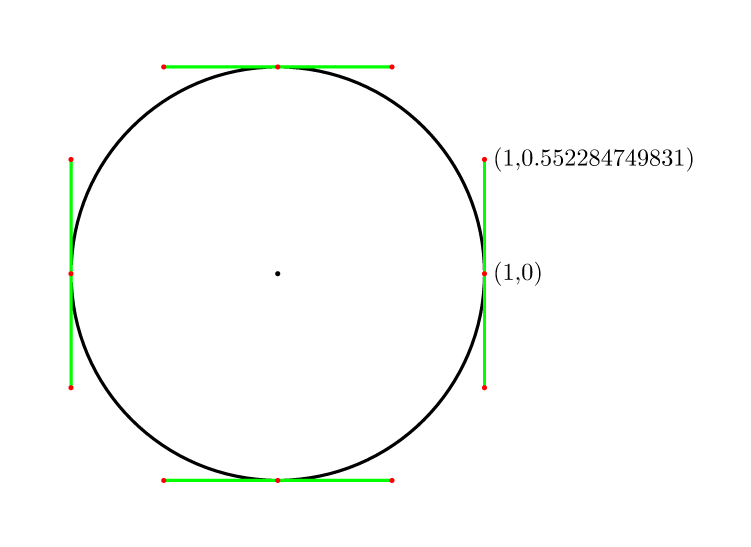
Интересно, что кривые Безье могут приближаться к кругу, но не совсем подходят по кругу. Общее приближение состоит в том, чтобы использовать четыре безье для моделирования круга, каждый с контрольными точками на расстоянии d=r*4*(sqrt(2)-1)/3 от конечных точек (где r - радиус круга), и в направление, касательное к окружности в конечных точках. Это обеспечит, что средние точки Безье находятся на круге, а первая производная непрерывна.
Радиальная погрешность в этом приближении составит около 0,0273% от радиуса круга.
Michael Goldapp, "Приближение дуг окружности кубическими полиномами". Компьютерный геометрический дизайн (#8 1991, стр.227-238)
Тор Доккен и Мортен Дэлен, "Хорошие приближения окружностей кривыми Безье, непрерывными по кривизне", Геометрический дизайн с помощью компьютера (№ 7, 1990, с. 33-41). http://www.sciencedirect.com/science/article/pii/016783969090019N (статья не бесплатная)
Также см. Статью о неоплачиваемой работе по адресу http://spencermortensen.com/articles/bezier-circle/
Браузеры и Холст Элемент.
Обратите внимание, что некоторые браузеры используют кривые Безье для своей дуги рисования холста, Chrome использует (в настоящее время) четырехсекторный подход, а Safari использует восьмисекторный подход, разница заметна только при высоком разрешении из-за этого 0,0273%, а также только действительно видимые, когда дуги нарисованы параллельно и не в фазе, вы заметите, что дуги колеблются от истинного круга. Эффект также более заметен, когда кривая анимируется вокруг своего радиального центра, радиус 600px обычно является размером, в котором он будет иметь значение.
Некоторые API рисования не имеют истинного рендеринга дуг, поэтому они также используют кривые Безье, например, платформа Flash не имеет API рисования дуг, поэтому любые платформы, которые предлагают дуги, обычно используют один и тот же подход кривой Безье.
Обратите внимание, что движки SVG в браузерах могут использовать другой метод рисования.
Другие платформы
Независимо от платформы, которую вы пытаетесь использовать, стоит проверить, как выполняется дуговое рисование, чтобы вы могли прогнозировать подобные визуальные ошибки и адаптироваться.
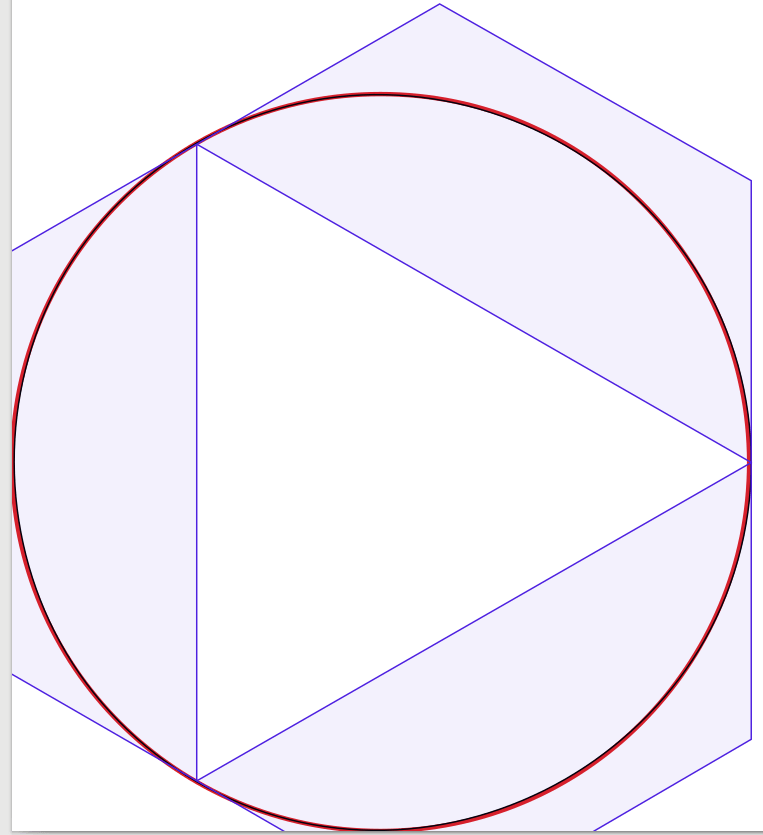
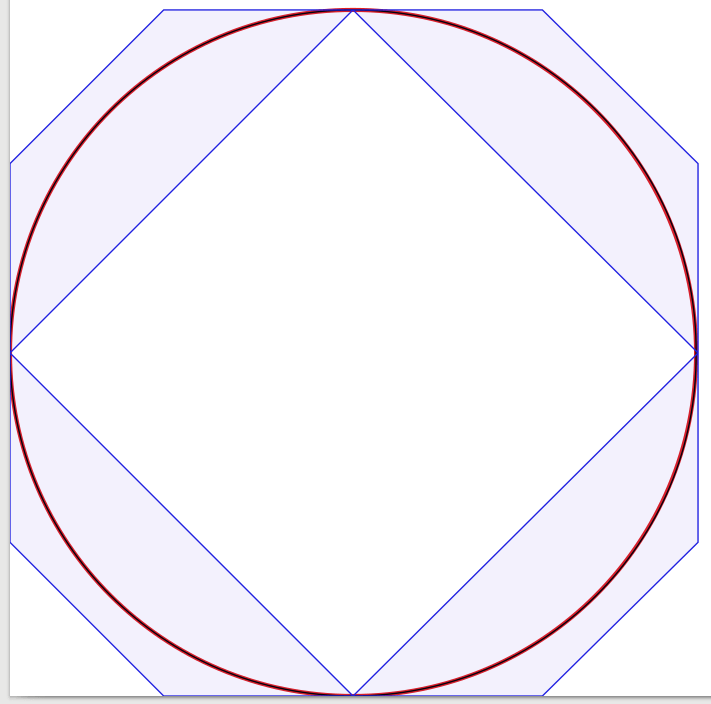
Ответы на вопрос очень хорошие, поэтому добавить нечего. Вдохновленный этим, я начал проводить эксперимент, чтобы визуально подтвердить решение, начиная с четырех кривых Безье, уменьшая количество кривых до одной. Удивительно, но я обнаружил, что с тремя кривыми Безье круг выглядел достаточно хорошо для меня, но конструкция немного сложнее. На самом деле я использовал Inkscape, чтобы поместить черное приближение Безье шириной в 1 пиксель на красный круг шириной в 3 пикселя (как в Inkscape). Для пояснения я добавил синие линии и поверхности, показывающие ограничивающие рамки кривых Безье.
Чтобы увидеть себя, я представляю свои результаты:
1-кривой график (который выглядит как капля, сжатая в углу, только для полноты): 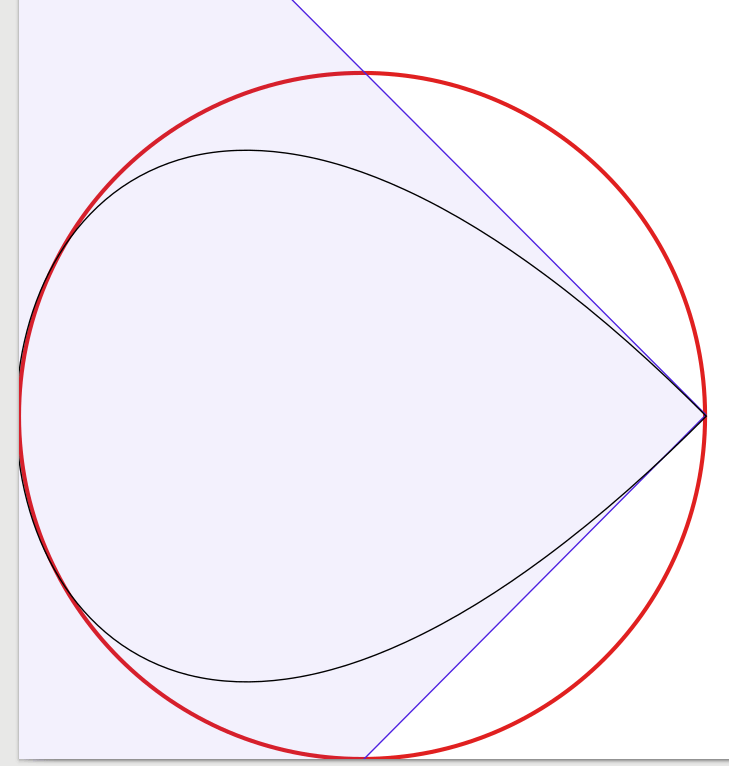
(Я хотел разместить SVG или PDF здесь, но это не поддерживается)
Для людей, которые просто ищут код:
https://jsfiddle.net/nooorz24/2u9forep/12/
var c = document.getElementById("myCanvas");
var ctx = c.getContext("2d");
function drawBezierOvalQuarter(centerX, centerY, sizeX, sizeY) {
ctx.beginPath();
ctx.moveTo(
centerX - (sizeX),
centerY - (0)
);
ctx.bezierCurveTo(
centerX - (sizeX),
centerY - (0.552 * sizeY),
centerX - (0.552 * sizeX),
centerY - (sizeY),
centerX - (0),
centerY - (sizeY)
);
ctx.stroke();
}
function drawBezierOval(centerX, centerY, sizeX, sizeY) {
drawBezierOvalQuarter(centerX, centerY, -sizeX, sizeY);
drawBezierOvalQuarter(centerX, centerY, sizeX, sizeY);
drawBezierOvalQuarter(centerX, centerY, sizeX, -sizeY);
drawBezierOvalQuarter(centerX, centerY, -sizeX, -sizeY);
}
function drawBezierCircle(centerX, centerY, size) {
drawBezierOval(centerX, centerY, size, size)
}
drawBezierCircle(200, 200, 64)<canvas id="myCanvas" width="400" height="400" style="border:1px solid #d3d3d3;">
Your browser does not support the HTML5 canvas tag.</canvas>Это позволяет нарисовать круг, который состоит из 4 кривых Безье. Написано на JS, но может быть легко переведено на любой другой язык
Уже много ответов, но я нашел небольшую онлайн-статью с очень хорошим приближением кубического Безье к кругу. В единицах окружности с = 0,55191502449, где с - расстояние от точек пересечения оси вдоль касательных к контрольным точкам.
В качестве одного квадранта для единичного круга с двумя средними координатами, являющимися контрольными точками. (0,1),(c,1),(1,c),(1,0)
Радиальная ошибка составляет всего 0,019608%, поэтому мне просто нужно было добавить ее в этот список ответов.
Статью можно найти здесь Приблизительный круг с кубическими кривыми Безье
Это невозможно. Безье - это кубика (по крайней мере... чаще всего используется). Круг не может быть выражен точно с кубикой, потому что круг содержит квадратный корень в своем уравнении. Как следствие, вы должны приблизиться.
Для этого вы должны разделить свой круг на n-tants (например, квадранты, октанты). Для каждого n-танта вы используете первую и последнюю точку в качестве первой и последней кривой Безье. Многоугольник Безье требует двух дополнительных точек. Чтобы быть быстрым, я бы взял касательные к кругу для каждой крайней точки n-танта и выбрал две точки как пересечение двух касательных (так что в основном ваш многоугольник Безье является треугольником). Увеличьте количество n-tants, чтобы соответствовать вашей точности.
Другие ответы охватывают тот факт, что истинный круг невозможен. Этот SVG-файл является аппроксимацией с использованием квадратичных кривых Безье и является наиболее близким, что вы можете получить: http://en.wikipedia.org/wiki/File:Circle_and_quadratic_bezier.svg
Вот один с кривыми Кубического Безье: http://en.wikipedia.org/wiki/File:Circle_and_cubic_bezier.svg
Я не уверен, стоит ли мне открывать новый вопрос, поскольку речь идет об аппроксимации, но меня интересует общая формула для получения контрольных точек для Безье любой степени, и я считаю, что она вписывается в этот вопрос. Все решения, которые я нашел в интернете, предназначены только для кубических кривых или платные, или я даже не понимаю (я не очень хорош в математике). Поэтому я решил попытаться решить это самостоятельно. Я изучал расстояние от контрольной точки до центра круга в зависимости от заданного угла и до сих пор обнаружил, что:
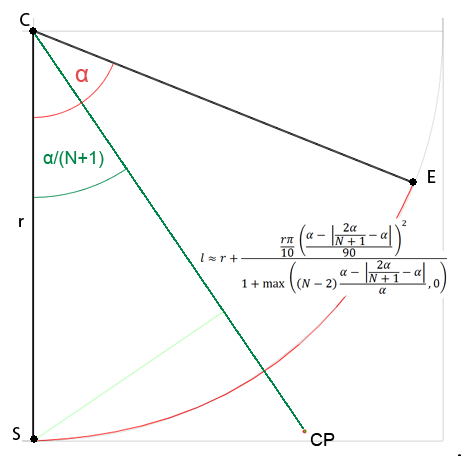
куда N количество контрольных точек для одной кривой и α угол дуги окружности.
Для квадратичной кривой это можно упростить до l ≈ r + r * PI*0.1 * pow(α/90, 2)PI*0.1 скорее предположение - я не рассчитал идеальную стоимость, но это довольно близко. Это работает достаточно хорошо для кривой с 1-2 контрольными точками, дающими погрешность радиуса около 0,2% для кубической кривой. Для кривых более высокой степени потеря точности заметна. С 3 контрольными точками кривая похожа на квадратичную, так что, очевидно, я что-то упускаю, но не могу понять, и этот метод в целом соответствует моим потребностям. Вот демо.
Если вам нужна чистая JS-версия ответа user7689607Это вернет путь SVG:
function drawBezierOvalQuarter(centerX, centerY, sizeX, sizeY) {
return `
M ${centerX - sizeX} ${centerY}
C ${centerX - sizeX} ${centerY - 0.552 * sizeY},
${centerX - 0.552 * sizeX} ${centerY - sizeY},
${centerX} ${centerY - sizeY}
`;
}
function drawBezierOval(centerX, centerY, sizeX, sizeY) {
return (
drawBezierOvalQuarter(centerX, centerY, -sizeX, sizeY) +
drawBezierOvalQuarter(centerX, centerY, sizeX, sizeY) +
drawBezierOvalQuarter(centerX, centerY, sizeX, -sizeY) +
drawBezierOvalQuarter(centerX, centerY, -sizeX, -sizeY)
);
}
Извините, что вернул это из мертвых, но я нашел этот пост очень полезным вместе с этой страницей, чтобы придумать расширяемую формулу.
По сути, вы можете создать ближний круг, используя невероятно простую формулу, которая позволяет использовать любое количество кривых Безье свыше 4: Distance = radius * stepAngle / 3
куда Distance расстояние между контрольной точкой Безье и ближайшим концом дуги, радиус radius круга и stepAngle это угол между двумя концами дуги, представленный 2π / (количество кривых).
Таким образом, чтобы поразить это в один выстрел: Distance = radius * 2π / (the number of curves) / 3
Это тяжелое приближение, которое будет выглядеть разумным или ужасным в зависимости от разрешения и точности, но я использую sqrt(2)/2 x radius в качестве контрольных точек. Я прочитал довольно длинный текст, как получается это число, и его стоит прочитать, но приведенная выше формула быстрая и грязная.