Использование atan2 для нахождения угла между двумя векторами
Я это понимаю:
atan2(vector.y, vector.x) = угол между вектором и осью X.
Но я хотел знать, как получить угол между двумя векторами, используя atan2. Итак, я наткнулся на это решение:
atan2(vector1.y - vector2.y, vector1.x - vector2.x)
Мой вопрос очень прост:
Будут ли две следующие формулы давать одно и то же число?
atan2(vector1.y - vector2.y, vector1.x - vector2.x)atan2(vector2.y - vector1.y, vector2.x - vector1.x)
Если нет: как узнать, какой вектор стоит первым в вычитаниях?
Спасибо
9 ответов
atan2(vector1.y - vector2.y, vector1.x - vector2.x)
это угол между вектором разности (соединяющим vector2 и vector1) и осью x, что, вероятно, не то, что вы имели в виду.
(Направленный) угол от вектора 1 до вектора 2 может быть вычислен как
angle = atan2(vector2.y, vector2.x) - atan2(vector1.y, vector1.x);
и вы можете нормализовать его в диапазоне 0 .. 2 * Pi:
if (angle < 0) angle += 2 * M_PI;
Правильный способ сделать это - найти синус угла с помощью перекрестного произведения и косинус угла с помощью точечного произведения и объединить их с Atan2() функция.
В C# это
public struct Vector2
{
public double X, Y;
/// <summary>
/// Returns the angle between two vectos
/// </summary>
public static double GetAngle(Vector2 A, Vector2 B)
{
// |A·B| = |A| |B| COS(θ)
// |A×B| = |A| |B| SIN(θ)
return Math.Atan2(Cross(A,B), Dot(A,B));
}
public double Magnitude { get { return Math.Sqrt(Dot(this,this)); } }
public static double Dot(Vector2 A, Vector2 B)
{
return A.X*B.X+A.Y*B.Y;
}
public static double Cross(Vector2 A, Vector2 B)
{
return A.X*B.Y-A.Y*B.X;
}
}
class Program
{
static void Main(string[] args)
{
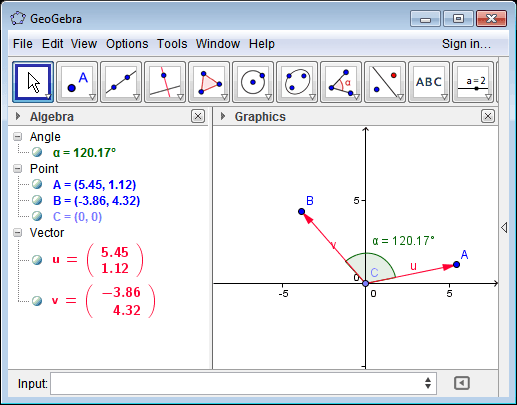
Vector2 A=new Vector2() { X=5.45, Y=1.12};
Vector2 B=new Vector2() { X=-3.86, Y=4.32 };
double angle=Vector2.GetAngle(A, B) * 180/Math.PI;
// angle = 120.16850967865749
}
}
Смотрите тестовый пример выше в GeoGebra.
Я думаю, что лучшая формула была размещена здесь: http://www.mathworks.com/matlabcentral/answers/16243-angle-between-two-vectors-in-3d
angle = atan2(norm(cross(a,b)), dot(a,b))
Таким образом, эта формула работает в 2 или 3 измерениях. Для двух измерений эта формула упрощается до указанной выше.
Никто не указал, что если у вас есть один вектор, и вы хотите найти угол вектора от оси X, вы можете воспользоваться тем фактом, что аргумент atan2() на самом деле является наклоном линии, или (дельта Y / delta X). Так что, если вы знаете наклон, вы можете сделать следующее:
дано:
A = угол вектора / линии, которую вы хотите определить (от оси X).
m = знаковый наклон вектора / линии.
затем:
A = atan2 (м, 1)
Очень полезно!
В качестве дополнения к ответу @martin-r следует отметить, что для arcus tangens можно использовать формулу суммы / разности.
angle = atan2(vec2.y, vec2.x) - atan2(vec1.y, vec1.x);
angle = -atan2(vec1.x * vec2.y - vec1.y * vec2.x, dot(vec1, vec2))
where dot = vec1.x * vec2.x + vec1.y * vec2.y
- Предупреждение 1: убедитесь, что угол остается в пределах -pi ... +pi
- Предостережение 2: остерегайтесь, когда векторы становятся очень похожими, вы можете получить вымирание в первом аргументе, что приведет к неточностям в цифрах
Если вы заботитесь о точности для малых углов, вы хотите использовать это:
угол = 2*atan2(|| ||b||a - ||a||b ||, || ||b||a + ||a||b ||)
Где "||" означает абсолютное значение, ака "длина вектора". См. https://math.stackexchange.com/questions/1143354/numerically-stable-method-for-angle-between-3d-vectors/1782769
Однако у этого есть недостаток: в двух измерениях он теряет знак угла.
angle(vector.b,vector.a)=pi/2*((1+sgn(xa))*(1-sgn(ya^2))-(1+sgn(xb))*(1-sgn(yb^2)))
+pi/4*((2+sgn(xa))*sgn(ya)-(2+sgn(xb))*sgn(yb))
+sgn(xa*ya)*atan((abs(xa)-abs(ya))/(abs(xa)+abs(ya)))
-sgn(xb*yb)*atan((abs(xb)-abs(yb))/(abs(xb)+abs(yb)))
xb,yb и xa,ya - координаты двух векторов
Вот небольшая программа на Python, которая использует угол между векторами, чтобы определить, находится ли точка внутри или снаружи определенного многоугольника
import sys
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches
from shapely.geometry import Point, Polygon
from pprint import pprint
# Plot variables
x_min, x_max = -6, 12
y_min, y_max = -3, 8
tick_interval = 1
FIG_SIZE = (10, 10)
DELTA_ERROR = 0.00001
IN_BOX_COLOR = 'yellow'
OUT_BOX_COLOR = 'black'
def angle_between(v1, v2):
""" Returns the angle in radians between vectors 'v1' and 'v2'
The sign of the angle is dependent on the order of v1 and v2
so acos(norm(dot(v1, v2))) does not work and atan2 has to be used, see:
https://stackru.com/questions/21483999/using-atan2-to-find-angle-between-two-vectors
"""
arg1 = np.cross(v1, v2)
arg2 = np.dot(v1, v2)
angle = np.arctan2(arg1, arg2)
return angle
def point_inside(point, border):
""" Returns True if point is inside border polygon and False if not
Arguments:
:point: x, y in shapely.geometry.Point type
:border: [x1 y1, x2 y2, ... , xn yn] in shapely.geomettry.Polygon type
"""
assert len(border.exterior.coords) > 2,\
'number of points in the polygon must be > 2'
point = np.array(point)
side1 = np.array(border.exterior.coords[0]) - point
sum_angles = 0
for border_point in border.exterior.coords[1:]:
side2 = np.array(border_point) - point
angle = angle_between(side1, side2)
sum_angles += angle
side1 = side2
# if wn is 1 then the point is inside
wn = sum_angles / 2 / np.pi
if abs(wn - 1) < DELTA_ERROR:
return True
else:
return False
class MainMap():
@classmethod
def settings(cls, fig_size):
# set the plot outline, including axes going through the origin
cls.fig, cls.ax = plt.subplots(figsize=fig_size)
cls.ax.set_xlim(-x_min, x_max)
cls.ax.set_ylim(-y_min, y_max)
cls.ax.set_aspect(1)
tick_range_x = np.arange(round(x_min + (10*(x_max - x_min) % tick_interval)/10, 1),
x_max + 0.1, step=tick_interval)
tick_range_y = np.arange(round(y_min + (10*(y_max - y_min) % tick_interval)/10, 1),
y_max + 0.1, step=tick_interval)
cls.ax.set_xticks(tick_range_x)
cls.ax.set_yticks(tick_range_y)
cls.ax.tick_params(axis='both', which='major', labelsize=6)
cls.ax.spines['left'].set_position('zero')
cls.ax.spines['right'].set_color('none')
cls.ax.spines['bottom'].set_position('zero')
cls.ax.spines['top'].set_color('none')
@classmethod
def get_ax(cls):
return cls.ax
@staticmethod
def plot():
plt.tight_layout()
plt.show()
class PlotPointandRectangle(MainMap):
def __init__(self, start_point, rectangle_polygon, tolerance=0):
self.current_object = None
self.currently_dragging = False
self.fig.canvas.mpl_connect('key_press_event', self.on_key)
self.plot_types = ['o', 'o-']
self.plot_type = 1
self.rectangle = rectangle_polygon
# define a point that can be moved around
self.point = patches.Circle((start_point.x, start_point.y), 0.10,
alpha=1)
if point_inside(start_point, self.rectangle):
_color = IN_BOX_COLOR
else:
_color = OUT_BOX_COLOR
self.point.set_color(_color)
self.ax.add_patch(self.point)
self.point.set_picker(tolerance)
cv_point = self.point.figure.canvas
cv_point.mpl_connect('button_release_event', self.on_release)
cv_point.mpl_connect('pick_event', self.on_pick)
cv_point.mpl_connect('motion_notify_event', self.on_motion)
self.plot_rectangle()
def plot_rectangle(self):
x = [point[0] for point in self.rectangle.exterior.coords]
y = [point[1] for point in self.rectangle.exterior.coords]
# y = self.rectangle.y
self.rectangle_plot, = self.ax.plot(x, y,
self.plot_types[self.plot_type], color='r', lw=0.4, markersize=2)
def on_release(self, event):
self.current_object = None
self.currently_dragging = False
def on_pick(self, event):
self.currently_dragging = True
self.current_object = event.artist
def on_motion(self, event):
if not self.currently_dragging:
return
if self.current_object == None:
return
point = Point(event.xdata, event.ydata)
self.current_object.center = point.x, point.y
if point_inside(point, self.rectangle):
_color = IN_BOX_COLOR
else:
_color = OUT_BOX_COLOR
self.current_object.set_color(_color)
self.point.figure.canvas.draw()
def remove_rectangle_from_plot(self):
try:
self.rectangle_plot.remove()
except ValueError:
pass
def on_key(self, event):
# with 'space' toggle between just points or points connected with
# lines
if event.key == ' ':
self.plot_type = (self.plot_type + 1) % 2
self.remove_rectangle_from_plot()
self.plot_rectangle()
self.point.figure.canvas.draw()
def main(start_point, rectangle):
MainMap.settings(FIG_SIZE)
plt_me = PlotPointandRectangle(start_point, rectangle) #pylint: disable=unused-variable
MainMap.plot()
if __name__ == "__main__":
try:
start_point = Point([float(val) for val in sys.argv[1].split()])
except IndexError:
start_point= Point(0, 0)
border_points = [(-2, -2),
(1, 1),
(3, -1),
(3, 3.5),
(4, 1),
(5, 1),
(4, 3.5),
(5, 6),
(3, 4),
(3, 5),
(-0.5, 1),
(-3, 1),
(-1, -0.5),
]
border_points_polygon = Polygon(border_points)
main(start_point, border_points_polygon)
Вам не нужно использовать atan2 для вычисления угла между двумя векторами. Если вы просто хотите самый быстрый способ, вы можете использовать dot(v1, v2)=|v1|*|v2|*cos Aполучить
A = Math.acos( dot(v1, v2)/(v1.length()*v2.length()) );
Формула, angle(vector.b,vector.a), что я отправил, дайте результаты
в четырех квадрантах и для любых координат xa,ya а также xb,yb,
Для координат xa=ya=0 и или xb=yb=0 не определено
Угол может быть больше или меньше, чем piи может быть положительным
или отрицательный.