Почему GHC исправляет ошибки?

Question

Глядя на исходный код GHC, я вижу, что определение для исправления:

fix :: (a -> a) -> a
fix f = let x = f x in x

В примере исправление используется так:

fix (\f x -> let x' = x+1 in x:f x')

Это в основном дает последовательность чисел, которые увеличиваются на единицу до бесконечности. Чтобы это произошло, исправление должно быть карри в функции, которую он получает, обратно к той самой функции в качестве первого параметра. Мне не ясно, как определение исправления, перечисленное выше, могло бы сделать это.

Это определение, как я понял, как работает исправление:

fix :: (a -> a) -> a
fix f = f (fix f)

Итак, теперь у меня есть два вопроса:

1. Как x означает " исправить x" в первом определении?
2. Есть ли преимущество в использовании первого определения перед вторым?

Answer 1

Легко увидеть, как работает это определение, применяя эквациональные рассуждения.

fix :: (a -> a) -> a
fix f = let x = f x in x

Что будет x оценивать, когда мы пытаемся оценить fix f? Это определяется как f x, так fix f = f x, Но что это x Вот? Это f xтак же, как и раньше. Итак, вы получаете fix f = f x = f (f x), Рассуждая таким образом, вы получаете бесконечную цепочку приложений f: fix f знак равно f (f (f (f ...))),

Теперь, заменяя (\f x -> let x' = x+1 in x:f x') за f ты получаешь

fix (\f x -> let x' = x+1 in x:f x')
    = (\f x -> let x' = x+1 in x:f x') (f ...)
    = (\x -> let x' = x+1 in x:((f ...) x'))
    = (\x -> x:((f ...) x + 1))
    = (\x -> x:((\x -> let x' = x+1 in x:(f ...) x') x + 1))
    = (\x -> x:((\x -> x:(f ...) x + 1) x + 1))
    = (\x -> x:(x + 1):((f ...) x + 1))
    = ...

Изменить: Относительно вашего второго вопроса, @is7s указал в комментариях, что первое определение предпочтительнее, потому что оно более эффективно.

Чтобы узнать почему, давайте посмотрим на ядро ​​для fix1 (:1) !! 10^8:

a_r1Ko :: Type.Integer    
a_r1Ko = __integer 1

main_x :: [Type.Integer]   
main_x =
  : @ Type.Integer a_r1Ko main_x

main3 :: Type.Integer
main3 =
  !!_sub @ Type.Integer main_x 100000000

Как видите, после преобразований fix1 (1:) по сути стал main_x = 1 : main_x, Обратите внимание, как это определение относится к самому себе - это то, что означает "завязывание узла". Эта самостоятельная ссылка представляется как простая косвенная указатель во время выполнения:

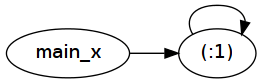
Теперь давайте посмотрим на fix2 (1:) !! 100000000:

main6 :: Type.Integer
main6 = __integer 1

main5
  :: [Type.Integer] -> [Type.Integer]
main5 = : @ Type.Integer main6

main4 :: [Type.Integer]
main4 = fix2 @ [Type.Integer] main5

main3 :: Type.Integer
main3 =
  !!_sub @ Type.Integer main4 100000000

Здесь fix2 Приложение на самом деле сохраняется:

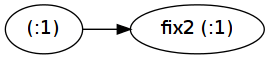
В результате вторая программа должна выполнить выделение для каждого элемента списка (но, поскольку список сразу используется, программа по-прежнему эффективно работает в постоянном пространстве):

$ ./Test2 +RTS -s
   2,400,047,200 bytes allocated in the heap
         133,012 bytes copied during GC
          27,040 bytes maximum residency (1 sample(s))
          17,688 bytes maximum slop
               1 MB total memory in use (0 MB lost due to fragmentation)
 [...]

Сравните это с поведением первой программы:

$ ./Test1 +RTS -s          
          47,168 bytes allocated in the heap
           1,756 bytes copied during GC
          42,632 bytes maximum residency (1 sample(s))
          18,808 bytes maximum slop
               1 MB total memory in use (0 MB lost due to fragmentation)
[...]

Answer 2

Как x означает "исправить x" в первом определении?

fix f = let x = f x in x

Пусть привязки в Хаскеле рекурсивны

Прежде всего, следует понимать, что Haskell допускает рекурсивные привязки let. То, что Haskell называет "let", некоторые другие языки называют "letrec". Это выглядит вполне нормально для определений функций. Например:

ghci> let fac n = if n == 0 then 1 else n * fac (n - 1) in fac 5
120

Но это может показаться довольно странным для определения значений. Тем не менее, значения могут быть определены рекурсивно из-за нестрогости Хаскелла.

ghci> take 5 (let ones = 1 : ones in ones)
[1,1,1,1,1]

См. Подробное введение в разделы 3.3 и 3.4 Haskell для более подробной информации о лени Haskell.

Thunks в GHC

В GHC выражение, еще не оцененное, обернуто в "thunk": обещание выполнить вычисление. Thunks оцениваются только тогда, когда они обязательно должны быть. Предположим, мы хотим fix someFunction, Согласно определению fix, это

let x = someFunction x in x

Теперь GHC видит что-то вроде этого.

let x = MAKE A THUNK in x

Так что он радостно делает для вас гром и движется прямо, пока вы не потребуете знать, что x на самом деле

Образец оценки

Выражение этого толка как раз и относится к самому себе. Давайте возьмем ones пример и переписать его для использования fix,

ghci> take 5 (let ones recur = 1 : recur in fix ones)
[1,1,1,1,1]

Так как же будет выглядеть этот пух?
Мы можем встроить ones как анонимная функция \recur -> 1 : recur для более четкой демонстрации.

take 5 (fix (\recur -> 1 : recur))

-- expand definition of fix
take 5 (let x = (\recur -> 1 : recur) x in x)

Теперь то, что x? Ну, хотя мы не совсем уверены, что x есть, мы все еще можем пройти через приложение функции:

take 5 (let x = 1 : x in x)

Эй, смотри, мы вернулись к определению, которое у нас было раньше.

take 5 (let ones = 1 : ones in ones)

Так что, если вы верите, что понимаете, как это работает, то у вас есть хорошее представление о том, как fix работает.

---

Есть ли преимущество в использовании первого определения перед вторым?

Да. Проблема в том, что вторая версия может вызвать утечку пространства даже при оптимизации. Смотрите GHC trac ticket # 5205, для аналогичной проблемы с определением forever, Вот почему я упомянул Thunks: потому что let x = f x in x выделяет только один ствол: x санк.

Answer 3

Разница в том, чтобы делиться с копированием.¹

fix1 f = x where x = f x    -- more visually apparent way to write the same thing

fix2 f = f (fix2 f)

Если мы подставим определение в себя, оба уменьшатся как одна и та же бесконечная цепочка приложений f (f (f (f (f ...)))), Но первое определение использует явное именование; в Haskell (как и в большинстве других языков) совместное использование обеспечивается возможностью называть вещи: одно имя более или менее гарантированно ссылается на одну "сущность" (здесь, x). 2-е определение не гарантирует какого-либо обмена - результат вызова fix2 f подставляется в выражение, поэтому оно может быть заменено значением.

Но данный компилятор теоретически может быть умным и использовать совместное использование во втором случае.

С этим связан вопрос "Y комбинатор". В нетипизированном лямбда-исчислении, где нет конструкций именования (и, следовательно, нет самореференции), Y- комбинатор эмулирует самоссылку, организуя копирование определения, так что ссылка на копию себя становится возможной. Но в реализациях, которые используют модель среды для разрешения именованных сущностей в языке, становится возможной прямая ссылка по имени.

Чтобы увидеть более резкую разницу между двумя определениями, сравните

fibs1 = fix1 ( (0:) . (1:) . g ) where g (a:t@(b:_)) = (a+b):g t
fibs2 = fix2 ( (0:) . (1:) . g ) where g (a:t@(b:_)) = (a+b):g t

Смотрите также:

• В Схеме, как вы используете лямбда для создания рекурсивной функции?
• У комбинатора обсуждение в "Маленьком интриганке"
• Можно ли использовать fold для создания бесконечных списков?

(особенно попробуйте проработать два последних определения в последней ссылке выше).

---

¹ Работа с определениями, для вашего примера fix (\g x -> let x2 = x+1 in x : g x2) мы получаем

fix1 (\g x -> let x2 = x+1 in x : g x2)
 = fix1 (\g x -> x : g (x+1))
 = fix1 f where {f = \g x -> x : g (x+1)}
 = fix1 f where {f g x = x : g (x+1)}
 = x      where {x = f x ; f g x = x : g (x+1)}
 = g      where {g = f g ; f g x = x : g (x+1)}   -- both g in {g = f g} are the same g
 = g      where {g = \x -> x : g (x+1)}           -- and so, here as well
 = g      where {g x = x : g (x+1)}

и, следовательно, правильное рекурсивное определение для g на самом деле создан. (выше мы пишем ....x.... where {x = ...} за let {x = ...} in ....x....для разборчивости).

Но второй вывод происходит с решающим отличием замены значения, а не имени, как

fix2 (\g x -> x : g (x+1))
 = fix2 f             where {f g x = x : g (x+1)}
 = f (fix2 f)         where {f g x = x : g (x+1)}
 = (\x-> x : g (x+1)) where {g = fix2 f ; f g x = x : g (x+1)}
 = h                  where {h   x = x : g (x+1) ; g = fix2 f   ; f g x = x : g (x+1)}

поэтому фактический вызов будет продолжаться как, например,

take 3 $ fix2 (\g x -> x : g (x+1)) 10
 = take 3 (h 10)      where {h   x = x : g (x+1) ; g = fix2 f   ; f g x = x : g (x+1)}
 = take 3 (x:g (x+1)) where {x = 10 ;              g = fix2 f   ; f g x = x : g (x+1)}
 = x:take 2 (g x2)    where {x2 = x+1 ; x = 10 ;   g = fix2 f   ; f g x = x : g (x+1)}
 = x:take 2 (g x2)    where {x2 = x+1 ; x = 10 ; g = f (fix2 f) ; f g x = x : g (x+1)}
 = x:take 2 (x2 : g2 (x2+1))   where {             g2 = fix2 f  ;
                             x2 = x+1 ; x = 10 ;                  f g x = x : g (x+1)}
 = ......

и мы видим, что новая привязка (для g2) устанавливается здесь, вместо предыдущего (для gповторное использование как с fix1 определение.

Answer 4

У меня есть, возможно, немного упрощенное объяснение, которое исходит от встраивания оптимизации. Если у нас есть

fix :: (a -> a) -> a
fix f = f (fix f)

затем fix является рекурсивной функцией, и это означает, что она не может быть встроена в местах, где она используется (INLINE Прагма будет игнорироваться, если дано).

тем не мение

fix' f = let x = f x in x

не является рекурсивной функцией - она ​​никогда не вызывает сама себя. Только x внутри рекурсивно. Так что при звонке

fix' (\r x -> let x' = x+1 in x:r x')

компилятор может вставить его в

(\f -> (let y = f y in y)) (\r x -> let x' = x+1 in x:r x')

а затем продолжить упрощение, например,

let y = (\r x -> let x' = x+1 in x:r x') y in y 
let y = (\  x -> let x' = x+1 in x:y x')   in y 

что так же, как если бы функция была определена с использованием стандартной рекурсивной записи без fix:

    y       x =  let x' = x+1 in x:y x'