У комбинатора обсуждение в "Маленьком интриганке"

Question

Итак, я потратил много времени, читая и перечитывая окончание главы 9 в "Маленьком интрижке", где разработан аппликативный комбинатор Y для length функция. Я думаю, что моя путаница сводится к одному утверждению, которое контрастирует с двумя версиями длины (до того, как комбинатор выделен):

A:
  ((lambda (mk-length)
     (mk-length mk-length))
   (lambda (mk-length)
     (lambda (l)
       (cond
         ((null? l) 0 )
         (else (add1
                ((mk-length mk-length)
                 (cdr l))))))))

B:
((lambda (mk-length)
      (mk-length mk-length))
    (lambda (mk-length)
      ((lambda (length)
         (lambda (l)
           (cond
             ((null? l) 0)
             (else (add1 (length (cdr l)))))))
       (mk-length mk-length))))

Страница 170 (4-е изд.) Утверждает, что

возвращает функцию, когда мы применили ее к аргументу

пока Б

не возвращает функцию

таким образом производя бесконечный регресс само-приложений. Я озадачен этим. Если B страдает от этой проблемы, я не вижу, как A избегает этого.

Answer 1

Отличный вопрос В интересах тех, у кого нет работающей установки DrRacket (включая меня), я постараюсь ответить на него.

Во-первых, давайте использовать здравые имена, легко отслеживаемые человеческим глазом / разумом:

((lambda (h)     ; A.   
     (h h))            ; apply h on h
 (lambda (g)
     (lambda (lst)
       (if (null? lst) 0
         (add1 
               ((g g) (cdr lst)))))))

Первый лямбда-термин - это то, что известно как комбинатор омега. Когда применяется к чему-либо, это вызывает самоприменение этого термина. Таким образом, вышесказанное эквивалентно

(let ((h (lambda (g)
           (lambda (lst)
             (if (null? lst) 0
               (add1 ((g g) (cdr lst))))))))
  (h h))

когда h применяется на h, новая привязка формируется:

(let ((h (lambda (g)
           (lambda (lst)
             (if (null? lst) 0
               (add1 ((g g) (cdr lst))))))))
  (let ((g h))
    (lambda (lst)
            (if (null? lst) 0
              (add1 ((g g) (cdr lst)))))))

Теперь больше нечего применять, поэтому внутренний lambda форма возвращается вместе со скрытыми связями с фреймами среды (т. е. теми, которые позволяют привязкам) над ней.

Такое сочетание лямбда-выражения с определяющим его окружением известно как замыкание. Для внешнего мира это просто еще одна функция одного параметра, lst, На данный момент больше не осталось шагов сокращения.

Теперь, когда это закрытие - наш list-length функция - будет вызвана, выполнение в конечном итоге достигнет точки (g g) Самостоятельное применение, и снова будут выполнены те же этапы восстановления, как указано выше. Но не раньше.

---

Теперь авторы этой книги хотят прийти к комбинатору Y, поэтому они применяют некоторые преобразования кода к первому выражению, чтобы как-то организовать это самоприменение (g g) будет выполняться автоматически - так что мы можем написать приложение рекурсивной функции в обычном порядке, (f x) вместо того, чтобы писать это как ((g g) x) для всех рекурсивных вызовов:

((lambda (h)     ; B.
     (h h))            ; apply h on h
 (lambda (g)
   ((lambda (f)           ; 'f' to become bound to '(g g)',
      (lambda (lst) 
        (if (null? lst) 0
          (add1 (f (cdr lst))))))  ; here: (f x) instead of ((g g) x)!
    (g g))))                       ; (this is not quite right)

Теперь после нескольких шагов сокращения мы приходим к

(let ((h (lambda (g)
           ((lambda (f)    
              (lambda (lst) 
                (if (null? lst) 0
                  (add1 (f (cdr lst))))))
            (g g)))))
  (let ((g h))
    ((lambda (f)
       (lambda (lst)
            (if (null? lst) 0
              (add1 (f (cdr lst))))))
     (g g))))

что эквивалентно

(let ((h (lambda (g)
           ((lambda (f)    
              (lambda (lst) 
                (if (null? lst) 0
                  (add1 (f (cdr lst))))))
            (g g)))))
  (let ((g h))
    (let ((f (g g)))           ; problem! (under applicative-order evaluation)
       (lambda (lst)
            (if (null? lst) 0
              (add1 (f (cdr lst))))))))

И тут приходит беда: самоприменение (g g) выполняется слишком рано, прежде чем эта внутренняя лямбда может быть даже возвращена в качестве замыкания в систему времени выполнения. Мы хотим уменьшить его, только когда выполнение дошло до той точки внутри лямбда-выражения, после того как было вызвано замыкание. Уменьшать его до того, как замыкание даже создано, смешно. Тонкая ошибка.:)

Конечно, так как g связан с h, (g g) сводится к (h h) и мы вернулись снова, где мы начали, применяя h на h, Циклический.

---

Конечно, авторы знают об этом. Они хотят, чтобы и мы это поняли.

Таким образом, виновник прост - это аппликативный порядок оценки: оценка аргумента до того, как будет сформирована привязка из формального параметра функции и значения ее аргумента.

Это преобразование кода было не совсем правильным. Это работало бы в обычном порядке, где аргументы не оцениваются заранее.

Это достаточно легко исправить с помощью " eta-extension ", которое задерживает приложение до фактической точки вызова: (lambda (x) ((g g) x)) на самом деле говорит: "позвоню ((g g) x) когда вызвано с аргументом x ".

И это на самом деле то, что это преобразование кода должно было быть в первую очередь:

((lambda (h)     ; C.
     (h h))            ; apply h on h
 (lambda (g)
   ((lambda (f)           ; 'f' to become bound to '(lambda (x) ((g g) x))',
      (lambda (lst) 
        (if (null? lst) 0
          (add1 (f (cdr lst))))))  ; here: (f x) instead of ((g g) x)
    (lambda (x) ((g g) x)))))

Теперь можно выполнить следующий шаг сокращения:

(let ((h (lambda (g)
           ((lambda (f)    
              (lambda (lst) 
                (if (null? lst) 0
                  (add1 (f (cdr lst))))))
            (lambda (x) ((g g) x))))))
  (let ((g h))
    (let ((f (lambda (x) ((g g) x))))
      (lambda (lst)
            (if (null? lst) 0
              (add1 (f (cdr lst))))))))

и закрытие (lambda (lst) ...) формируется и возвращается без проблем, а когда (f (cdr lst)) называется (внутри замыкания) он уменьшается до ((g g) (cdr lst)) как мы и хотели.

---

Наконец, мы замечаем, что (lambda (f) (lambda (lst ...)) выражение в C. не зависит ни от одного из h а также g, Таким образом, мы можем убрать это, сделать это аргументом и остаться с... Y комбинатором:

( ( (lambda (rec)            ; D.
      ( (lambda (h) (h h))  
        (lambda (g)
          (rec (lambda (x) ((g g) x))))))   ; applicative-order Y combinator
    (lambda (f)    
        (lambda (lst) 
          (if (null? lst) 0
            (add1 (f (cdr lst)))))) )
  (list 1 2 3) )                            ; ==> 3

Итак, теперь вызов Y для функции эквивалентен созданию из нее рекурсивного определения:

( y (lambda (f) (lambda (x) .... (f x) .... )) ) 
===  define f = (lambda (x) .... (f x) .... )

... но используя letrec (или с именем let) лучше - более эффективно, определяя замыкание в фрейме самореферентной среды. Вся вещь Y является теоретическим упражнением для систем, где это невозможно - то есть, когда невозможно назвать вещи, создать привязки с именами, "указывающими" на вещи, ссылающимися на вещи.

Кстати, способность указывать на вещи - это то, что отличает высших приматов от остальных живых существ животного царства, или, как я слышал.:)

Answer 2

Чтобы увидеть, что происходит, используйте степпер в DrRacket. Степпер позволяет увидеть все промежуточные шаги (и переходить назад и вперед).

Вставьте следующее в DrRacket:

(((lambda (mk-length)
    (mk-length mk-length))
  (lambda (mk-length)
    (lambda (l)
      (cond
        ((null? l) 0 )
        (else (add1
               ((mk-length mk-length)
                (cdr l))))))))
 '(a b c))

Затем выберите язык обучения "Средний студент с лямбдой". Затем нажмите кнопку "шаговый" (зеленый треугольник и полоса).

Вот как выглядит первый шаг:

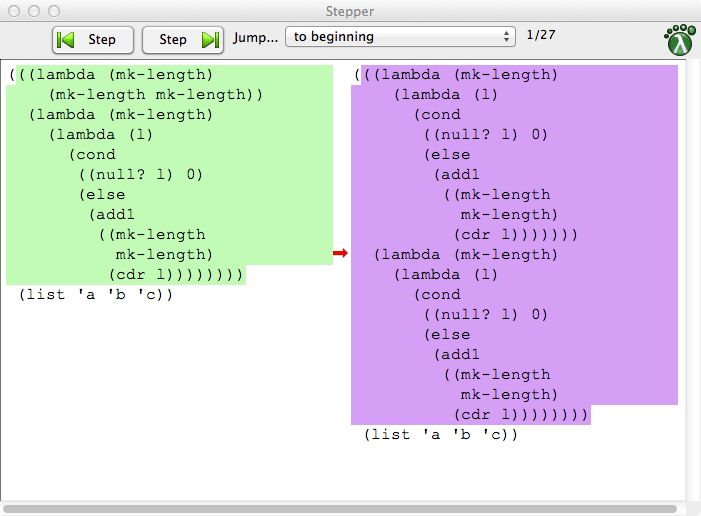
Затем создайте пример для второй функции и посмотрите, что не так.