Невыпуклый многоугольник - препроцесс для использования алгоритма выпуклой оболочки
Я использовал алгоритм выпуклого Халла, чтобы найти контур для некоторой... неправильной формы. Это не достаточно хорошо, хотя...
Вполне возможно, потому что я не могу гарантировать, что моя форма выпуклая...
У меня есть набор прямоугольников, и я хотел бы иметь возможность получить все точки на внешней стороне контура, но не выбрасывать ни одну из точек контура.
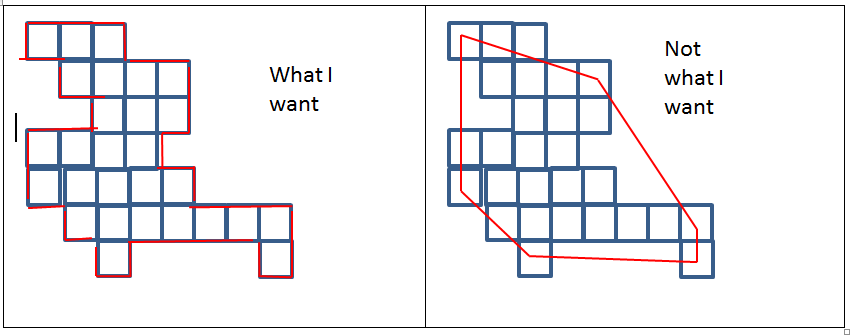
Алгоритм выпуклой оболочки отлично работает, но работает как в примере справа, поэтому я теряю некоторую информацию о контурах.
Я хочу что-то, что работает ближе к версии слева, сохраняя внешние углы, и только устраняя точки внутри...
Есть ли такой алгоритм?
Или есть ли способ разбить такую форму (многоугольник) на выпуклые формы, чтобы алгоритм выпуклой оболочки мог ее правильно обработать?
От ссылки к ссылке я пытался выяснить, как настроить какой-то алгоритм, такой как алгоритм Хертеля-Мелхорна - но я не знаю, как использовать пересекающиеся линии в этой ситуации...
Спасибо за любое предложение.
1 ответ
Если ваш невыпуклый многоугольник такой, каким вы его показали (т. Е. Объединение набора четырехугольных элементов), все, что вам нужно сделать, это найти ребра четырехугольников, которые лежат на границе.
Этого можно достичь, отметив, что эти "внешние" ребра появляются только в одном элементе, тогда как "внутренние" ребра являются общими для двух соседних элементов. Это подразумевает следующий простой алгоритм:
edge_list = {}
for (i = all elements in mesh)
for (j = all edges in element(i))
edge_list <- push jth edge of ith element
endfor
endfor
edge_list <- sort
edge_list <- remove_duplicates
Оставшиеся уникальные ребра образуют внешний контур вашего многоугольника. Этот простой алгоритм работает в O(N*log(N)) время.
Вы можете улучшить сложность, используя подходящую хеш-таблицу для сравнения ребер, уменьшая сложность до O(N),