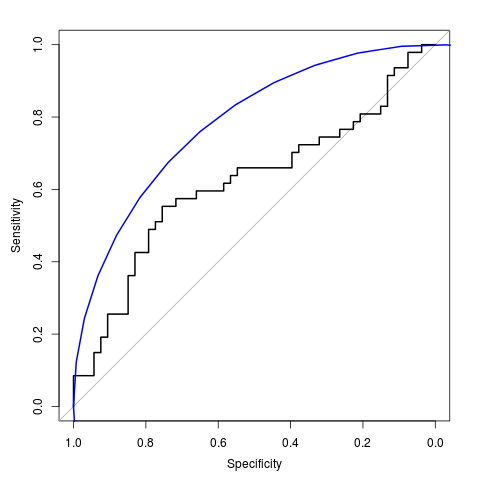
Добавление произвольной кривой с AUC 0.8 к графику ROC

Question

У меня есть простой ROC-график, который я создаю с помощью пакета pROC:

plot.roc(response, predictor)

Он работает нормально, как и ожидалось, но я хотел бы добавить эталонную кривую "идеальной" формы с AUC 0.8 для сравнения (AUC моего графика ROC составляет 0.66).

Какие-нибудь мысли?

Просто чтобы прояснить, я не пытаюсь сгладить свой график ROC, но пытаюсь добавить опорную кривую, которая представляла бы AUC 0.8 (аналогично диагональной линии, представляющей AUC 0.5).

Answer 1

Упоминание диагональная линия имеет смысл (модель, которая угадывает случайным образом), так что вы бы так же должны определить модель, связанную с эталонной кривой AUC 0,8. Различные модели будут связаны с разными эталонными кривыми.

Например, можно определить модель, для которой прогнозируемые вероятности равномерно распределены между 0 и 1, а для точки с прогнозируемой вероятностью p вероятность истинного исхода равна p^k для некоторой константы k. Оказывается, что для этой модели k=2 дает график с AUC 0,8.

library(pROC)
set.seed(144)
probs <- seq(0, 1, length.out=10000)
truth <- runif(10000)^2 < probs
plot.roc(truth, probs)
# Call:
# plot.roc.default(x = truth, predictor = probs)
# 
# Data: probs in 3326 controls (truth FALSE) < 6674 cases (truth TRUE).
# Area under the curve: 0.7977

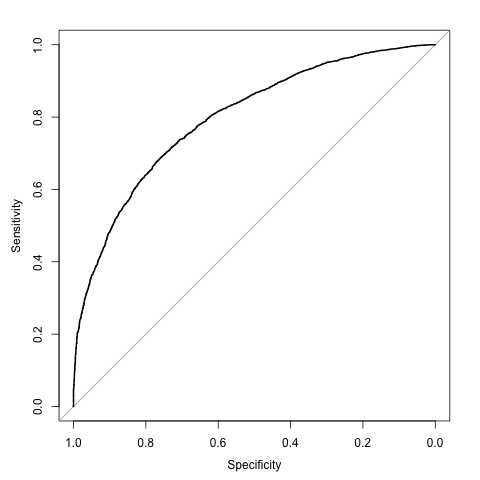
Некоторая алгебра показывает, что это конкретное семейство моделей имеет AUC (2+3k)/(2+4k), что означает, что она может генерировать кривые с AUC между 0,75 и 1 в зависимости от значения k.

Другой подход, который вы можете использовать, связан с логистической регрессией. Если бы у вас было значение функции линейного предиктора логистической регрессии p, то есть вы бы предсказали вероятность 1/(1+exp(-p)), тогда вы могли бы пометить истинный результат как истинный, если p плюс некоторый нормально распределенный шум превышает 0, а иначе пометить истинный результат как ложный. Если нормально распределенный шум имеет дисперсию 0, ваша модель будет иметь AUC 1, а если нормально распределенный шум имеет дисперсию, приближающуюся к бесконечности, ваша модель будет иметь AUC 0,5.

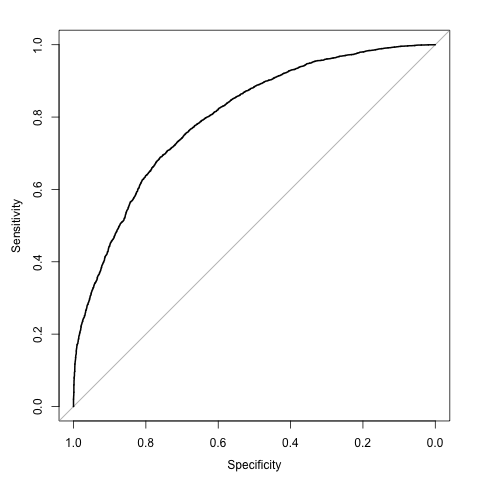
Если я предполагаю, что исходные прогнозы основаны на стандартном нормальном распределении, то похоже, что нормально распределенный шум со стандартным отклонением 1,2 дает AUC 0,8 (хотя я не мог найти хорошую замкнутую форму для AUC):

set.seed(144)
pred.fxn <- rnorm(10000)
truth <- (pred.fxn + rnorm(10000, 0, 1.2)) >= 0
plot.roc(truth, pred.fxn)
# Call:
# plot.roc.default(x = truth, predictor = pred.fxn)
# 
# Data: pred.fxn in 5025 controls (truth FALSE) < 4975 cases (truth TRUE).
# Area under the curve: 0.7987

Answer 2

Быстрый / грубый способ - добавить круг с радиусом 1 на график, который будет иметь AUC pi/4 = 0,7853982.

library(pROC)
library(car)

n <- 100L

x1 <- rnorm(n, 2.0, 0.5)
x2 <- rnorm(n, -1.0, 2)
y <- rbinom(n, 1L, plogis(-0.4 + 0.5 * x1 + 0.1 * x2))

mod <- glm(y ~ x1 + x2, "binomial")
probs <- predict(mod, type = "response")

plot(roc(y, probs))
ellipse(c(0, 0), matrix(c(1,0,0,1), 2, 2), radius = 1, center.pch = FALSE, col = "blue")