Гауссовская случайная функция

Question

Используя normrnd, я хотел бы создать функцию нормального распределения со средними и сигма-значениями, выраженными как векторы размером 1x45, варьирующимися от 1:45, и построить этот смоделированный PDF-файл с идеальными значениями.

Всякий раз, когда я создаю норм, как показано ниже,

Gaussian = normrnd([1 45],[1 45],[1 500],length(c_t));

Я получаю следующую ошибку,

Size information is inconsistent.

Причиной создания этого PDF является вычисление химической кинетики трассера с моделью переменного гауссовского шума. По сути, у меня есть идеальные характеристики трассера, теперь я хотел бы добавить гауссовский шум и понять, как химическая кинетика трассера меняется с изменением шума.

В основном, существуют различные вычислительные модели для понимания химической кинетики трассера, одна из которых - трехкомпонентная модель, другие - анализ формы, модель анализа ограниченной формы.

В настоящее время у меня есть идеальная кривая для всех соответствующих моделей, теперь я хотел бы добавить шум к этим моделям и понять, как каждая конкретная модель ведет себя с переменным шумом

Вот почему я хотел бы создать модель переменного шума с помощью normrnd, добавить эту модель к идеальным характеристикам и вычислить шум (сигма) в сравнении с ошибкой. Этот анализ даст мне приблизительную оценку того, как различные модели ведут себя с переменным шумом и какая модель подходит для оценка химической кинетики трассера.

function [c_t,c_t_noise] =Noise_ConstrainedK2(t,a1,a2,a3,b1,b2,b3,td,tmax,k1,k2,k3)

    K_1   = (k1*k2)/(k2+k3);
    K_2   = (k1*k3)/(k2+k3);
    %DV_free= k1/(k2+k3);

    c_t = zeros(size(t));
    ind = (t > td) & (t < tmax);
    c_t(ind)= conv(((t(ind) - td) ./ (tmax - td) * (a1 + a2 + a3)),(K_1*exp(-(k2+k3)*t(ind)+K_2)),'same');
    ind = (t >= tmax);

    c_t(ind)=conv((a1 * exp(-b1 * (t(ind) - tmax))+ a2 * exp(-b2 * (t(ind) - tmax))) + a3 * exp(-b3 * (t(ind) - tmax)),(K_1*exp(-(k2+k3)*t(ind)+K_2)),'same');

    meanAndVar = (rand(45,2)-0.5)*2;
    numPoints = 500;
    randSamples = zeros(1,numPoints);
    for ii = 1:numPoints
        idx = mod(ii,size(meanAndVar,1))+1;
        randSamples(ii) = normrnd(meanAndVar(idx,1),meanAndVar(idx,2));
        c_t_noise = c_t + randSamples(ii);
    end
    scatter(1:numPoints,randSamples)

    dg = [0 0.5 0];
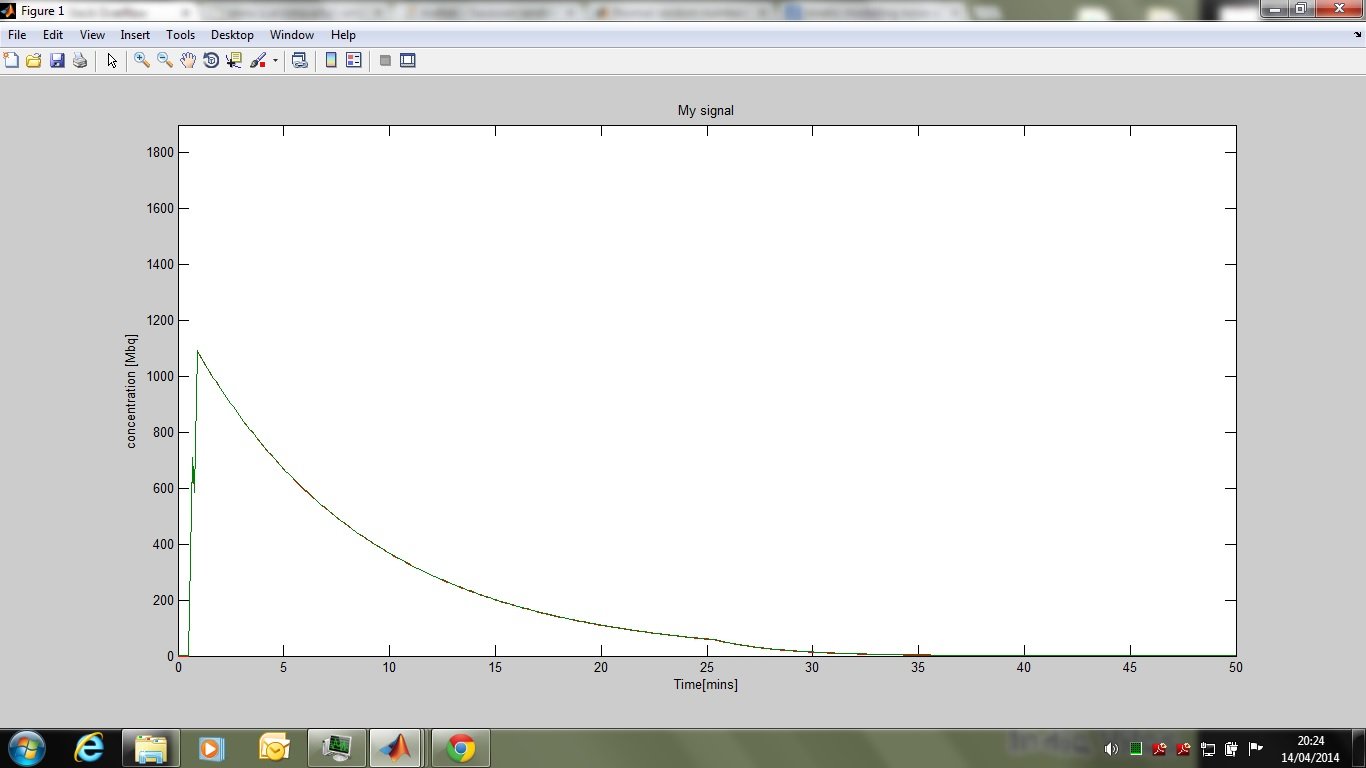
    plot(t,c_t,'r');
    hold on;
    plot(t,c_t_noise,'Color',dg);
    hold off; 

    axis([0 50 0 1900]);
    xlabel('Time[mins]');
    ylabel('concentration [Mbq]');
    title('My signal');

    %plot(t,c_tnp);
end

Выходные характеристики из вышеуказанной функции следующие: здесь я не мог визуализировать шум

Answer 1

Единственная дистанционно близкая вещь к тому, что вы хотите сделать, может быть выполнена следующим образом, но будет включать в себя циклы, потому что вы не можете запросить 500 точек данных только из 45 различных средних значений и отклонений, без предположения, что несколько наборов могут быть пересмотрены.

Это моя интерпретация того, что вы хотите, хотя я все еще не совсем уверен.

Случайный выбор функции Гаусса

meanAndVar = rand(45,2);
numPoints = 500;
randSamples = zeros(1,numPoints);
for ii = 1:numPoints
    randMeanVarIdx = randi([1,size(meanAndVar,1)]);
    randSamples(ii) = normrnd(meanAndVar(randMeanVarIdx,1),meanAndVar(randMeanVarIdx,2));
end
scatter(1:numPoints,randSamples)

Приведенный выше код генерирует случайную двумерную матрицу среднего и дисперсии (1-й столбец = среднее, 2-й столбец = дисперсия). Затем мы предварительно выделяем пространство.

Внутри цикла мы выбрали случайный набор среднего значения и дисперсии для использования (равномерно), а затем взяли это среднее значение и дисперсию, вставили его в функцию случайного значения Гаусса и сохранили ее.

матрица randSamples будет содержать список случайных значений, сгенерированных случайным набором гауссовских функций, выбранных случайным образом.

Последовательный выбор функции

Если вы не хотите случайным образом выбирать, какую функцию использовать, и просто хотите последовательно выполнять цикл, вы используете цикл для получения индекса того, какой набор значений использовать.

meanAndVar = (rand(45,2)-0.5)*2; % zero shift and make bounds [-1,1]
numPoints = 500;
randSamples = zeros(1,numPoints);
for ii = 1:numPoints
    idx = mod(ii,size(meanAndVar,1))+1;
    randSamples(ii) = normrnd(meanAndVar(idx,1),meanAndVar(idx,2));
end
scatter(1:numPoints,randSamples)

Answer 2

Проблема с этим утверждением

Gaussian = normrnd([1 45],[1 45],[1 500],length(c_t));

заключается в том, что вы предоставляете два значения mu и два сигма-значения и запрашиваете матрицу размера [1 500] x длина (c_t). Вы должны передать размер единообразным способом, так что либо

Gaussian = normrnd(mu, sigma,[500 length(c_t)]);

или же

Gaussian = normrnd(mu, sigma, 500, length(c_t));

Затем вы должны убедиться, что размер векторов mu/sigma соответствует размеру матрицы, которую вы запрашиваете. Поэтому, если вы хотите использовать матрицу 500 x length(c_t) в качестве выходных данных, вам нужно передать 500 x length(c_t) (mu,sigma) пар. Если вы хотите изменить только одно из значений mu или sigma, вы можете передать одно значение для другого параметра

Чтобы получить значения N из нормального распределения с фиксированным средним и постоянно увеличивающейся сигмой, вы можете сделать

noise = @(mu, s0, s1, n) normrnd(mu, s0:(s1-s0)/(n-1):s1, 1,n)

где s0 - самое низкое значение сигмы, а s1 - самое большое значение сигмы. Чтобы получить 10 значений, взятых из распределений с mu=0 и сигма-увеличением от 1 до 5, вы можете сделать

noise(0,1,5,10)

Если вы хотите внести некоторую случайность в увеличение сигмы, вы можете сделать

noise_rand = @(mu, s0, s1, n) normrnd(mu, (s0:(s1-s0)/(n-1):s1) .* rand(1,n), 1,n)