Z-Index без ограничений

Question

Мне нужно вычислить Z-индекс (Мортон) точки на плоскости по ее 2 координатам x, y.

Традиционно это просто решается с помощью чередования битов.

Тем не менее, у меня есть границы, и я хочу, чтобы z-индекс точки увеличивал количество минометов только тогда, когда он находится внутри активной области, и пропускал счет, когда находился снаружи.

Для ясности, типичный z-порядок в квадрате 4x4:

|  0  1  4  5 |
|  2  3  6  7 |
|  8  9 12 13 |
| 10 11 14 15 |

Однако, если у меня есть активная область 3x3, я хочу, чтобы индекс рассчитывался так:

|  0  1  4  x |
|  2  3  5  x |
|  6  7  8  x |
|  x  x  x  x |

Как вы можете видеть, заполнение четырехугольника 00-11, 02-13 пропускает счет для 2 точек, которые выходят за пределы активной области, то же самое для 20-31 и для 22-33.

Важно: я хочу сделать это без итерации.

Есть ли известное решение этой проблемы?

Answer 1

Мне удалось получить ответ на вопрос на https://fgiesen.wordpress.com/2009/12/13/decoding-morton-codes/

Чтобы обработать прямоугольные области, округлите все размеры до ближайшей степени 2 и сложите большую ось линейно.

Например, конечная точка (2,3) в прямоугольнике 5x4 выглядит следующим образом:

Округление 5x4 до ближайшей степени 2 дает 8x4, то есть 3 и 2 бита

Точка кодирования 2,3 Сначала чередуем 2 бита 0b010, 0b11 получаем 0b1110, а 3-й бит из измерения x становится 5-м битом результата.

Кодировка 4,2, 0b100, 0b11 становится 0b11010

Чтобы найти z-порядок области 3x3, найдите обратное отображение для области 4x4, используя описанный выше метод, обратный описанному выше, при создании карты пропустите все точки, которые выходят за пределы области 3x3.

отображение будет выглядеть

(0,0) -> (0,0)
(0,1) -> (1,0)
(0,2) -> (0,1)
(0,3) -> (1,1)
(1,0) -> (2,0)
(1,2) -> (2,1)
(2,0) -> (0,2)
(2,1) -> (1,2)
(3,0) -> (2,2)

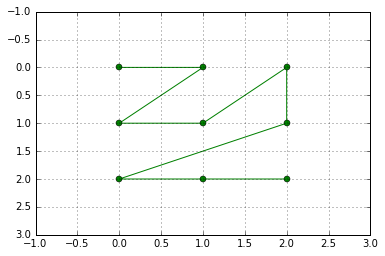Код Python может быть полезным, https://gist.github.com/kannaiah/4eb936b047a987b32555b2642a0979f7