Нахождение лучших путей k Viterbi в HMM
Мне нужно написать алгоритм, который находит топ-k пути Витерби в HMM (используя обычный алгоритм Витерби, чтобы найти лучший путь).
Я думаю, что мне, вероятно, нужно сохранить список V_t,N размера k для каждого состояния N, который содержит пути top-K, оканчивающиеся на состояние N, но я не совсем уверен, как отслеживать этот список... есть идеи? Спасибо
2 ответа
Мы можем решить это с некоторой осторожностью. Это легче всего увидеть, посмотрев на решетчатую структуру хмм:
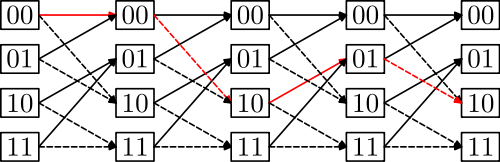
В этом примере скрытые состояния 00, 01, 10, 11 обозначают набор этих четырех как S. Наблюдения не показаны, но предполагают, что они равны 0,1.
Предположим, что у нас есть правильная матрица переходов:
transition[4][4]
Вероятности выбросов:
emissions[4][2]
И начальные вероятности:
p[2]
Таким образом, каждый столбец представляет скрытые состояния, и цель Витерби состоит в том, чтобы вычислить наиболее вероятную последовательность скрытых состояний с учетом наблюдений. Пусть теперь alpha(i, t) = наибольшая вероятность того, что скрытая последовательность состояний находится в состоянии i (i является одним из 00, 01, 10, 11), в момент t, когда наблюдение в момент t равно o_t (o_t равно единице 0, 1). Пусть первое наблюдение обозначено как o_1. Он может быть эффективно рассчитан как:
alpha(i, 1) = p[i] * emissions[i][o_1]
alpha(i, t) = emissions[i][o_t] * max_{k in states} (alpha(k, t-1) * transition[k][i])
Чтобы найти наилучший путь, мы сохраняем указатели в обратном направлении на шаге альфа (i, t), до состояния, в котором максимальная функция максимизирована выше. Наконец, мы просто исследуем все альфа (i, T) и i в состояниях, и находим, какой из них является наибольшим, а затем следуем за ним, чтобы получить наиболее вероятную последовательность состояний.
Теперь нам нужно расширить это для хранения лучших k-путей. В настоящее время в каждой альфе (i, t) мы храним только одного родителя. Однако предположим, что мы сохранили k лучших предшественников. Таким образом, каждая альфа (i, t) соответствует не только наиболее вероятному значению и узлу, с которого она перешла, но и списку верхних k узлов, с которых она могла перейти, и их значений в отсортированном порядке.
Это легко сделать, поскольку вместо выполнения max и взятия только одного предшествующего узла мы берем верхние k предшествующих узлов и сохраняем их. Теперь для базового случая нет предшествующего узла, поэтому альфа (i, 1) по-прежнему представляет собой только одно значение. Когда мы достигаем произвольного столбца (скажем, t) и хотим найти пути top-k, оканчивающиеся на узле (i) в этом столбце, мы должны найти лучшие k предшественников, которые должны быть получены, и верхние пути, которые нужно взять из них.
Это как если бы у нас была следующая проблема: матрица m размера 4 на k, где строка представляет предыдущее состояние, а m [состояние] представляет верхние k вероятностей для путей, заканчивающихся там. Таким образом, каждая строка m сортируется по наибольшему и наименьшему, теперь возникает проблема поиска:
Best_K_Values(t, i) = Top K over all i,preceding_state,k (emissions[i][o_t] * m[preceding_state][k] * transition[preceding_state][i])
Теперь это выглядит устрашающе, но потребуется некоторое время, чтобы понять это, мы можем решить проблему вершины k из отсортированной матрицы, используя кучу в O(4 log k) или O(numStates log k) в целом.
Посмотрите на это небольшое изменение Kth наименьшего элемента в отсортированной матрице, просто обратите внимание, что в нашем случае столбцы не отсортированы, но идея все еще применима.
Если вы все еще читаете, обратите внимание, что общая сложность этого метода составляет O((numStates log k) * numStates * t) = O(numStates^2 * t * log k) (я считаю, что это правильная сложность).
Это может быть трудно понять, но, пожалуйста, дайте мне знать, если у вас есть какие-либо вопросы, или я что-то сделал неправильно.
На самом деле об этом много литературы. Это заняло некоторое копание, но я нашел это.
Перечислите алгоритмы декодирования Витерби с приложениями
http://www.ensc.sfu.ca/people/faculty/cavers/ENSC805/readings/42comm02-seshadri.pdf